19.7: Angular Momentum and Torque for Fixed Axis Rotation
( \newcommand{\kernel}{\mathrm{null}\,}\)
We have shown that, for fixed axis rotation, the component of torque that causes the angular velocity to change is the rotational analog of Newton’s Second Law,
→τextS=IS→α
We shall now see that this is a special case of the more general result
→τextS=ddt→LsysS
Consider a rigid body rotating about a fixed axis passing through the point S and take the fixed axis of rotation to be the z -axis. Recall that all the points in the rigid body rotate about the z -axis with the same angular velocity →ω=(dθ/dt)ˆk=ωzˆk. In a similar fashion, all points in the rigid body have the same angular acceleration, →α=(d2θ/dt2)ˆk=αzˆk. Let the point S lie somewhere along the z -axis.
As before, the body is divided into individual elements. We calculate the contribution of each element to the angular momentum about the point S, and then sum over all the elements. The summation will become an integral for a continuous body.
Each individual element has a mass Δmj and is moving in a circle of radius r⊥S,j about the axis of rotation. Let →rS,j be the vector from the point S to the element. The momentum of the element, →pj, is tangent to this circle (Figure 19.16).
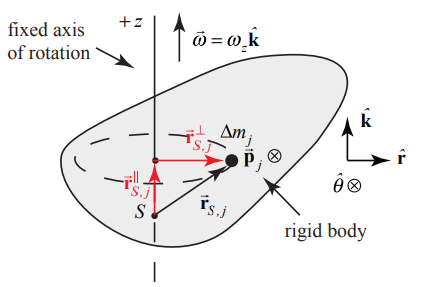
The angular momentum of the jth element about the point S is given by →LS,j=→rS,j×→pj. The vector →rS,j can be decomposed into parallel and perpendicular components with respect to the axis of rotation →rS,j=→r‖S,j+→r⊥S,j (Figure 19.16), where r⊥S,j=|→r⊥S,j| and r‖S,j=|→r‖S,j|. The momentum is given by →pj=Δmjr⊥S,jωzˆθ. Then the angular momentum about the point S is
→LS,j=→rS,j×→pj=(r⊥S,jˆr+r‖S,jˆk)×(Δmjr⊥S,jωzˆθ)=Δmj(r⊥S,j)2ωz−Δmjr‖S,jr⊥S,jωzˆr
In the last expression in Equation (19.5.22), the second term has a direction that is perpendicular to the z -axis. Therefore the z -component of the angular momentum about the point S, (LS,j)z, arises entirely from the second term, →r⊥S,j×→pj. Therefore the z -component of the angular momentum about S is
(LS,j)z=Δmj(r⊥S,j)2ωz
The z -component of the angular momentum of the system about S is the summation over all the elements,
LssS,z=∑j(Ls,j)z=∑jΔmj(r⊥s,j)2ωz
For a continuous mass distribution the summation becomes an integral over the body,
LsysS,z=∫bodydm(rdm)2ωz
where rdm is the distance form the fixed z -axis to the infinitesimal element of mass dm . The moment of inertia of a rigid body about a fixed z -axis passing through a point S is given by an integral over the body
IS=∫body dm(rdm)2
Thus the z -component of the angular momentum about S for a fixed axis that passes through S in the z -direction is proportional to the z -component of the angular velocity, ωz,
LsysS,z=ISωz
For fixed axis rotation, our result that torque about a point is equal to the time derivative of the angular momentum about that point,
→τextS=ddt→LsysS
can now be resolved in the z -direction,
τextS,z=dLsysS,zdt=ddt(ISωz)=ISdωzdt=ISd2θdt2=ISαz
in agreement with our earlier result that the z -component of torque about the point S is equal to the product of moment of inertia about IS and the z -component of the angular acceleration, αz.
Example 19.6 Circular Ring
A circular ring of radius R , and mass M is rotating about the z -axis in a plane parallel to but a distance h above the x-y plane. The z -component of the angular velocity is ωz (Figure 19.17). Find the magnitude and the direction of the angular momentum →LS along at any point S on the central z -axis.
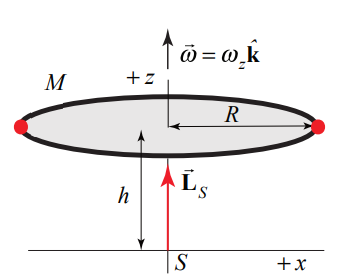
Solution: Use the same symmetry argument as we did in Example 19.5. The ring can be thought of as made up of pairs of point like objects on opposite sides of the ring each of mass m (Figure 19.18).
Each pair has a non-zero z-component of the angular momentum taken about any point S along the z -axis, →Lpair S=→LS,1+→LS,2=2mR2ωzˆk=mpairR2ωzˆk. The angular momentum of the ring about the point S is then the sum over all the pairs
→LS=∑paismpairR2ωzˆk=MR2ωzˆk
Recall that the moment of inertia of a ring is given by
IS=∫body dm(rdm)2=MR2
For the symmetric ring, the angular momentum about S points in the direction of the angular velocity and is equal to
→LS=ISωzˆk


