19.9: External Angular Impulse and Change in Angular Momentum
( \newcommand{\kernel}{\mathrm{null}\,}\)
Define the external angular impulse about a point S applied as the integral of the external torque about S
→JextS≡∫tfti→τextSdt
Then the external angular impulse about S is equal to the change in angular momentum
→JextS≡∫tfti→τextSdt=∫tftid→LsysSdtdt=→LsysS,f−→LsysS,i
Notice that this is the rotational analog to our statement about impulse and momentum,
→IextS≡∫tfti→Fextdt=∫tftid→psysdtdt=→psys,f−→psys,i
Example 19.9.1: Angular Impulse on Steel Washer
A steel washer is mounted on the shaft of a small motor. The moment of inertia of the motor and washer is I0. The washer is set into motion. When it reaches an initial angular speed ω0, at t = 0 , the power to the motor is shut off, and the washer slows down until it reaches an angular speed of ωa at time ta. At that instant, a second steel washer with a moment of inertia Iw is dropped on top of the first washer. Assume that the second washer is only in contact with the first washer. The collision takes place over a time Δtint=tb−ta. Assume the frictional torque on the axle is independent of speed, and remains the same when the second washer is dropped. The two washers continue to slow down during the time interval Δt2=tf−tb until they stop at time t=tf. (a) What is the angular acceleration while the washer and motor are slowing down during the interval Δt1=ta? (b) Suppose the collision is nearly instantaneous, Δtint=(tb−ta)≃0. What is the angular speed ωb of the two washers immediately after the collision is finished (when the washers rotate together)?
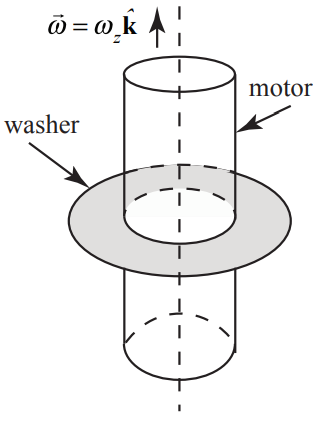
Now suppose the collision is not instantaneous but that the frictional torque is independent of the speed of the rotor. (c) What is the angular impulse during the collision? (d) What is the angular velocity ωb of the two washers immediately after the collision is finished (when the washers rotate together)? (e) What is the angular deceleration α2 after the collision?
Solution
a) The angular acceleration of the motor and washer from the instant when the power is shut off until the second washer was dropped is given by
α1=ωa−ω0Δt1<0
(b) If the collision is nearly instantaneous, then there is no angular impulse and therefore the z -component of the angular momentum about the rotation axis of the motor remains constant
0=ΔLz=Lf,z−L0,z=(I0+Iw)ωb−I0ωa
We can solve Equation (19.5.51) for the angular speed ωb of the two washers immediately after the collision is finished
ωb=I0I0+Iwωa
(c) The angular acceleration found in part a) is due to the frictional torque in the motor.
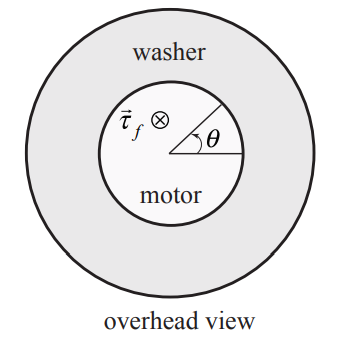
Let →τf=−τfˆk where τf is the magnitude of the frictional torque (Figure 19.25) then
−τf=I0α1=I0(ωa−ω0)Δt1
During the collision with the second washer, the frictional torque exerts an angular impulse (pointing along the z -axis in the figure),
Jz=−∫tbtaτfdt=−τfΔtint=I0(ωa−ω0)ΔtintΔt1
(d) The z -component of the angular momentum about the rotation axis of the motor changes during the collision,
ΔLz=Lf,z−L0,z=(I0+Iw)ωb−I0ωa
The change in the z -component of the angular momentum is equal to the z -component of the angular impulse
Jz=ΔLz
Thus, equating the expressions in Equations (19.5.54) and (19.5.55), yields
I0(ωa−ω0)(Δtint Δt1)=(I0+Iw)ωb−(I0)ωa
Solve Equation (19.5.57) for the angular velocity immediately after the collision,
ωb=I0(I0+Iw)((ωa−ω0)(ΔtintΔt1)+ωa)
If there were no frictional torque, then the first term in the brackets would vanish, and the second term of Equation (19.5.58) would be the only contribution to the final angular speed.
(e) The final angular acceleration α2 is given by
α2=0−ωbΔt2=−I0(I0+Iw)Δt2((ωa−ω0)(ΔtintΔt1)+ωa)


