10.5: Exercise Problems
( \newcommand{\kernel}{\mathrm{null}\,}\)
In each of Problems 10.1-10.3, for the given system:
(i) derive the Hamilton equations of motion, and
(ii) check whether the equations are equivalent to those derived from the Lagrangian formalism.
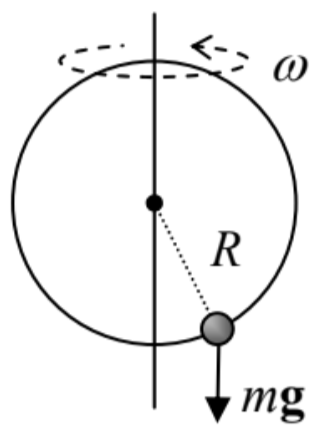
10.1. Our "testbed" system: a bead on a ring, being rotated with a fixed angular velocity ω about its vertical diameter − see Figure 2.1, reproduced on the right.
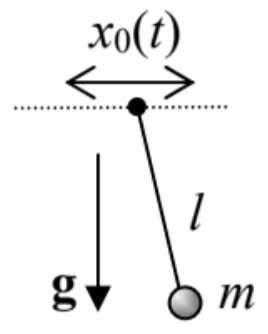
10.2. The system considered in Problem 2.3: a pendulum hanging from a horizontal support whose motion law x0(t) is fixed - see the figure on the right. (No vertical plane constraint.)
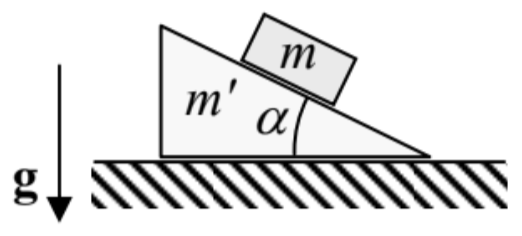
10.3. The system considered in Problem 2.8: a block of mass m that can slide, without friction, along the inclined surface of a heavy wedge of mass m ’. The wedge is free to move, also without friction, along a horizontal surface - see the figure on the right. (Both motions are within the vertical plane containing the steepest slope line.)
10.4. Find and solve the equations of motion of a particle with the following Hamiltonian function: H=12m(p+ar)2, where a is a constant scalar.
10.5. Let L be the Lagrangian function, and H the Hamiltonian function, of the same system. What three of the following four statements,
(i) dLdt=0,
(ii) ∂L∂t=0,
(iii) dHdt=0,
(iv) ∂H∂t=0,
are equivalent? Give an example when those three equalities hold, but the fourth one does not.
10.6. Calculate the Poisson brackets of a Cartesian component of the angular momentum L of a particle moving in a central force field and its Hamiltonian function H, and discuss the most evident implication of the result.
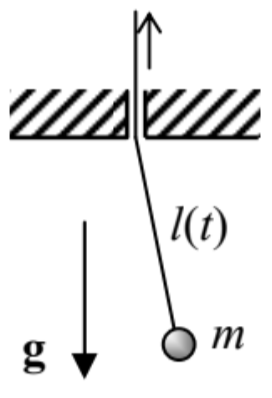
10.7. After small oscillations had been initiated in the point pendulum shown in Figure on the right, the string is being pulled up slowly, so that the pendulum’s length l is being reduced. Neglecting dissipation,
(i) prove by a direct calculation that the oscillation energy is indeed changing proportionately to the oscillation frequency, as it follows from the constancy of the corresponding adiabatic invariant (40); and
(ii) find the l-dependence of the amplitudes of the angular and linear deviations from the equilibrium.
10.8. The mass m of a small body that performs 1D oscillations in the potential well U(x)=ax2n, with n>0, is being changed slowly. Calculate the oscillation energy E as a function of m.
10.9. A stiff ball is bouncing vertically from the floor of an elevator whose upward acceleration changes very slowly. Neglecting the energy dissipation, calculate how much does the bounce height h change during the acceleration’s increase from 0 to g. Is your result valid for an equal but abrupt increase of the elevator’s acceleration?


