17.1: Particle in a Well

We begin with the one-dimensional case of a particle oscillating about a local minimum of the potential energy \(V(x)\). We’ll assume that near the minimum, call it \(x_{0}\) the potential is well described by the leading second-order term, \(V(x)=\frac{1}{2} V^{\prime \prime}\left(x_{0}\right)\left(x-x_{0}\right)^{2}\) so we’re taking the zero of potential at \(x_{0}\), assuming that the second derivative \(V^{\prime \prime}\left(x_{0}\right) \neq 0\), and (for now) neglecting higher order terms.

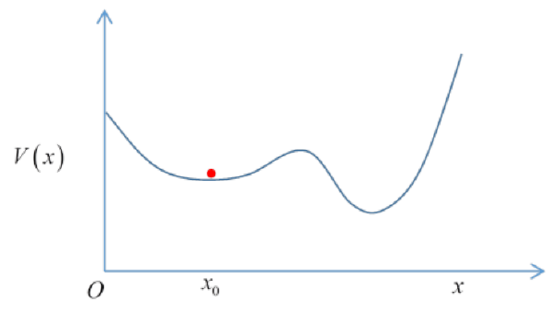
To simplify the equations, we’ll also move the \(x\) origin to \(x_{0}\), so

\begin{equation}
m \ddot{x}=-V^{\prime \prime}(0) x=-k x
\end{equation}

replacing the second derivative with the standard “spring constant” expression.

This equation has solution

\begin{equation}
x=A \cos (\omega t+\delta), \text { or } x=\operatorname{Re}\left(B e^{i \omega t}\right), \quad B=A e^{i \delta}, \quad \omega=\sqrt{k / m}
\end{equation}

(This can, of course, also be derived from the Lagrangian, easily shown to be \(L=\frac{1}{2} m \dot{x}^{2}-\frac{1}{2} m \omega^{2} x^{2}\).