25.4: Cylinder Rolling Inside another Cylinder

Last updated
Save as PDF

Page ID: 30535

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

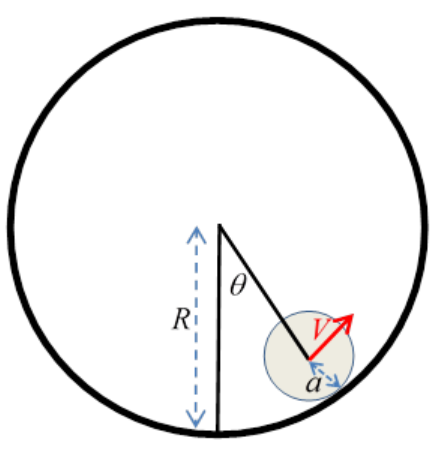
Now consider a solid cylinder radius a rolling inside a hollow cylinder radius R, angular distance from the lowest point \(\theta\), the solid cylinder axis moving at \(V=(R-a) \dot{\theta}\) and therefore having angular velocity (compute about the point of contact) \(\Omega=V / a\).

The kinetic energy is

\begin{equation}
\frac{1}{2} M V^{2}+\frac{1}{2} I(V / a)^{2}=\frac{1}{2}\left(M+\frac{I}{a^{2}}\right)(R-a)^{2} \dot{\theta}^{2}
\end{equation}

The potential energy is \(-M g(R-a) \cos \theta\).

The Lagrangian \(L=T-V\), the equation of motion is

\begin{equation}
\left(M+\frac{I}{a^{2}}\right)(R-a)^{2} \ddot{\theta}=-M g(R-a) \sin \theta \cong-M g(R-a) \theta
\end{equation}

so small oscillations are at frequency \(\omega=\sqrt{\frac{g}{\left(1+\frac{I}{M a^{2}}\right)(R-a)}}\).