27.4: Motion of Symmetrical Top around a Fixed Base with Gravity - Nutation

Denoting the distance of the center of mass from the fixed bottom point P as \(ℓ\) (along the axis) the moment of inertia about a line perpendicular to the axis at the base point is

\[I_{1}^{\prime}=I_{1}+M \ell^{2}\]

\(\left(I_{1}\right.\) being usual center of mass moment.)

The Lagrangian is ( P being the origin, \(I_{3}\) in direction \(\theta, \phi)\)

\[L=\frac{1}{2} I_{1}^{\prime}\left(\dot{\phi}^{2} \sin ^{2} \theta+\dot{\theta}^{2}\right)+\frac{1}{2} I_{3}(\dot{\phi} \cos \theta+\dot{\psi})^{2}-M g \ell \cos \theta\]

Notice that the coordinates \(\psi, \phi\) do not appear explicitly, so there are two constants of motion:

\[\begin{array}{l}
p_{\psi}=\partial L / \partial \dot{\psi}=I_{3}(\dot{\phi} \cos \theta+\dot{\psi})=L_{3} \\
p_{\phi}=\partial L / \partial \dot{\phi}=\left(I_{1}^{\prime} \sin ^{2} \theta+I_{3} \cos ^{2} \theta\right) \dot{\phi}+I_{3} \dot{\psi} \cos \theta=L_{Z}
\end{array}\]

That is, the angular momentum about \(x_{3}\) is conserved, because the two forces acting on the top, the gravitational pull at the center of mass and the floor reaction at the bottom point, both act along lines intersecting the axis, so never have torque about \(x_{3}\). The angular momentum about Z is conserved because the gravitational torque acts perpendicular to this line.

We have two linear equations in \(\dot{\psi}, \dot{\phi}\) with coefficients depending on \(\theta\) and the two constants of motion \(L_{3}, L_{Z}\). The solution is straightforward, giving

\[\dot{\phi}=\frac{L_{Z}-L_{3} \cos \theta}{I_{1}^{\prime} \sin ^{2} \theta}\]

and

\[ \dot{\psi}=\frac{L_{3}}{I_{3}}-\cos \theta\left(\frac{L_{Z}-L_{3} \cos \theta}{I_{1}^{\prime} \sin ^{2} \theta}\right)\]

The (conserved) energy

\[\begin{align} E &=\frac{1}{2} I_{1}^{\prime}\left(\Omega_{1}^{2}+\Omega_{2}^{2}\right)+\frac{1}{2} I_{3} \Omega_{3}^{2}+M g \ell \cos \theta \\[4pt]
&=\frac{1}{2} I_{1}^{\prime}\left(\dot{\phi}^{2} \sin ^{2} \theta+\dot{\theta}^{2}\right)+\frac{1}{2} I_{3}(\dot{\phi} \cos \theta+\dot{\psi})^{2}+M g \ell \cos \theta
\end{align}\]

Using the constants of motion to express \(\dot{\psi}, \dot{\phi}\) in terms of \(\theta\) and the constants \(L_{Z}, L_{3}\), then subtracting a \(\theta\) independent term to reduce clutter,

\[E^{\prime}=E-M g \ell-\left(L_{3}^{2} / 2 I_{3}\right)\]

we have

\[\begin{align*} E^{\prime} &= \frac{1}{2} I_{1}^{\prime} \dot{\theta}^{2}+V_{\mathrm{eff}}(\theta), \quad V_{\mathrm{eff}}(\theta) \\[4pt] &=\frac{\left(L_{Z}-L_{3} \cos \theta\right)^{2}}{2 I_{1}^{\prime} \sin ^{2} \theta}-M g \ell(1-\cos \theta) \end{align*}\]

The range of motion in \(\theta\) is given by \(E^{\prime}>V_{\mathrm{eff}}(\theta) . \text { For } L_{3} \neq L_{Z}, V_{\mathrm{eff}}(\theta)\) goes to infinity at \(\theta=0, \pi\) It has a single minimum between these points. (This isn’t completely obvious—one way to see it is to change variable to \(u=\cos \theta\), following Goldstein. Multiplying throughout by \(\sin ^{2} \theta\), and writing \(\dot{\theta}^{2} \sin ^{2} \theta=\dot{u}^{2}\) gives a one dimensional particle in a potential problem, and the potential is a cubic in \(u\). Of course some roots of \(E^{\prime}=V_{\mathrm{eff}}(\theta)\) could be in the unphysical region \(|u|>1\). In any case, there are at most three roots, so since the potential is positive and infinite at \(\theta=0, \pi\) it has at most two roots in the physical range.)

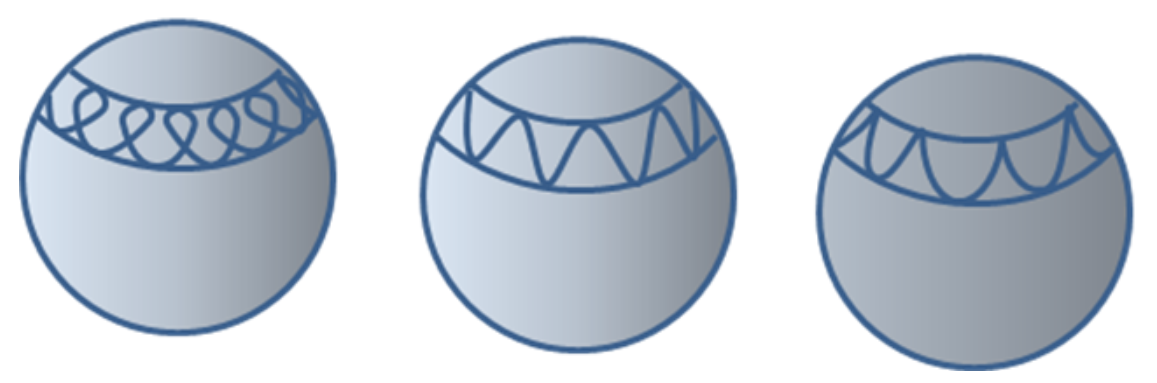
From the one-dimensional particle in a potential analogy, it’s clear that \(\theta\) oscillates between these two points \(\theta_{1} \text { and } \theta_{2}\). This oscillation is called nutation. Now

\[\dot{\phi}=\left(L_{Z}-L_{3} \cos \theta\right) / I_{1}^{\prime} \sin ^{2} \theta\]

could change sign during this oscillation, depending on whether or not the angle \(\cos ^{-1}\left(L_{Z} / L_{3}\right)\) is in the range. Visualizing the path of the top center point on a spherical surface centered at the fixed point, as it goes around it oscillates up and down, but if there is this sign change, it will “loop the loop”, going backwards on the top part of the loop.