30.2: Holonomic Constraints and non-Holonomic Constraints

A sphere rolling on a plane without slipping is constrained in its translational and rotational motion by the requirement that the point of the sphere momentarily in contact with the plane is at rest. How do we incorporate this condition in the dynamical analysis: the least action approach, for example, or the direct Newtonian equations of motion?

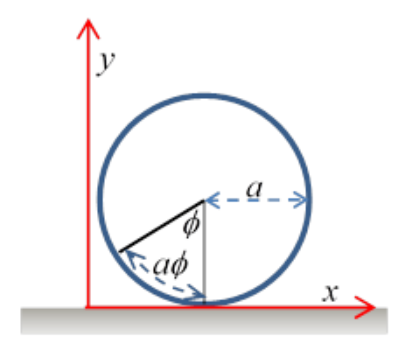
We’ll begin with a simpler example, that of a cylinder rolling in the x direction, its orientation \(\phi\) defined as zero as it passes the x origin, and its radius a. We see immediately that its orientation is uniquely given by its position (for no slipping) by \(x=a \phi, \text { or } v-a \dot{\phi}=0\). The constraint enables us to eliminate one of the dynamical variables from the equation. If we measure its position at some later time, we know the angle it turned through. The same argument works for a cylinder rolling inside a larger cylinder.

A constraint on a dynamical system that can be integrated in this way to eliminate one of the variables is called a holonomic constraint. A constraint that cannot be integrated is called a nonholonomic constraint.

For a sphere rolling on a rough plane, the no-slip constraint turns out to be nonholonomic.

To see this, imagine a sphere placed at the origin in the (x,y) plane. Call the point at the top of the sphere the North Pole. Now roll the sphere along the x axis until it has turned through ninety degrees. Its NS axis is now parallel to the x axis, the N pole pointing in the positive x direction. Now roll it through ninety degrees in a direction parallel to the y axis. The N pole is still pointing in the positive x direction, the sphere, taken to have unit radius, is at \((\pi / 2, \pi / 2)\).

Now start again at the origin, the N pole on top. This time, first roll the sphere through ninety degrees in the y direction. The N pole now points along the positive y axis. Next, roll the sphere through ninety degrees in the x direction: we’re back to the point \((\pi / 2, \pi / 2)\) but this time the N pole is pointing in the y direction.

The bottom line is that, in contrast to the cylindrical case, for a rolling sphere the no-slip constraint does not allow us to eliminate any dynamical variables—given that initially the sphere is at the origin with the N pole at the top, there is no unique relationship between orientation \((\theta, \phi)\) and position (x,y) at a later point, we would have to know the rolling history, and in fact we can roll back to the origin by a different route and in general the N pole will not be at the top when we return.

So the constraint equation, which can be written

\begin{equation}
\vec{V}-a \vec{\Omega} \times \vec{n}=0
\end{equation}

does not allow us to eliminate a variable, but it certainly plays a role in the dynamics! As we've seen, the identical equation for the cylinder, \(d x / d t-a d \phi / d t=0, \text { trivially integrates to } x=a \phi+c\), uniquely linking change in orientation with change in position. We see that for a ball rolling in two dimensions, there can be no such integral.

A possible approach is to use Lagrange multipliers to take account of the constraint, just as in deriving the equation for the catenary the fixed length of the string entered as a constraint. Doing this for the rolling ball turns out to lead to a very messy problem—for once, the advanced approach to dynamics doesn’t pay off. But there’s a better way.