30.6: Ball Rolling on Inclined Rotating Plane

Figure \(\PageIndex{1}\)

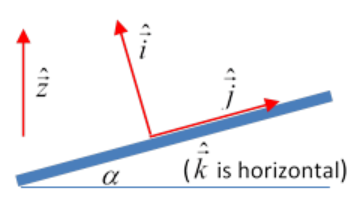
We’ll take unit vectors \(\begin{equation}\widehat{\vec{z}} \text { pointing vertically up, } \widehat{\vec{i}}\end{equation}\) perpendicularly up from the plane, the angle between these two unit vectors being α. (We will need a set of orthogonal unit vectors \(\widehat{\vec{i}}, \widehat{\vec{j}}, \widehat{\vec{k}}\), not fixed in the plane, but appropriately oriented, with \(\widehat{\vec{k}}\) horizontal.) The vector to the center of the sphere (radius \(a\), mass \(m\) ) from an origin on the axis of rotation, at a point a above the plane, is \(\vec{r}\). The contact reaction force of the plane on the sphere is \(\vec{R}\).

The equations of motion are:

\begin{equation}
m \ddot{\vec{r}}=\vec{R}-m g \widehat{\vec{z}}, \quad I \dot{\vec{\Omega}}=-a \widehat{\vec{i}} \times \vec{R}
\end{equation}

and the equation of rolling contact is \(\dot{\vec{r}} - a \vec{\Omega} \times \widehat{\vec{i}}=\widehat{\omega i} \times \vec{r}\).

First, we eliminate \(\vec{R}\) from the equations of motion to give

\begin{equation}
\dot{\vec{\Omega}}=(a m / I)(\ddot{\vec{r}}+g \widehat{\vec{z}}) \times \widehat{\vec{i}}
\end{equation}

Note that \(\dot{\vec{\Omega}} \cdot \widehat{\vec{i}}=0\), so the spin in the direction normal to the plane is constant, \(\vec{\Omega} \cdot \widehat{\vec{i}}=n\) say. (Both forces on the sphere have zero torque about this axis.)

Integrating,

\begin{equation}
\vec{\Omega}+\text { const. }=(m a / I)(\dot{\vec{r}}+g t\widehat{\vec{z}}) \times \widehat{\vec{i}}
\end{equation}

Now eliminate \(\vec{\Omega}\) by multiplying both sides by \(\times \vec{i}\) and using the equation of rolling contact

\begin{equation}
\dot{\vec{r}}-a \vec{\Omega} \times \widehat{\vec{i}}=\omega \widehat{\vec{i}} \times \vec{r}
\end{equation}

to find:

\begin{equation}
\left(m a^{2} / I\right)[(\dot{\vec{r}}+g t \widehat{\vec{z}}) \times \widehat{\vec{i}}] \times \widehat{\vec{i}}=a \vec{\Omega} \times \widehat{\vec{i}}+\text { const. }=\dot{\vec{r}}-\omega \widehat{\vec{i}} \times \vec{r}+\text { const. }
\end{equation}

then using \(\begin{equation}
(\dot{\vec{r}} \times \widehat{\vec{i}}) \times \widehat{\vec{i}}=-\dot{\vec{r}}, \; (\widehat{\vec{z}} \times \widehat{\vec{i}}) \times \widehat{\vec{i}}=-\widehat{\vec{j}}
\end{equation}\), we find

\begin{equation}
\dot{\vec{r}}\left(1+m a^{2} / I\right)+\left(m a^{2} / I\right) g t \widehat{\vec{j}} \sin \alpha+\text { const. }=\omega \widehat{vec{i}} \times \vec{r}
\end{equation}

The constant is fixed by the initial position \(\vec{r}_{0}\), giving finally

\begin{equation}
\dot{\vec{r}}=\dfrac{\omega}{1+m a^{2} / I} \widehat{\vec{i}} \times\left[\left(\vec{r}-\vec{r}_{0}\right)+\dfrac{m a^{2} / I}{\omega} g t \widehat{\vec{k}} \sin \alpha\right]
\end{equation}

The first term in the square brackets would give the same circular motion we found for the horizontal rotating plane, the second term adds a steady motion of the center of this circle, in a horizontal direction (not down the plane!) at constant speed \(\left(m a^{2} / I \omega\right) g \sin \alpha\).

(This is identical to the motion of a charged particle in crossed electric and magnetic fields.)

Bottom line: the intuitive notion that a ball rolling on a rotating inclined turntable would tend to roll downhill is wrong! Recall that for a particle circling in a magnetic field, if an electric field is added perpendicular to the magnetic field, the particle moves in a cycloid at the same average electrical potential—it has no net movement in the direction of the electric field , only perpendicular to it. Our rolling ball follows an identical cycloidal path—keeping the same average gravitational potential.