4.6: Differentiation Between Ordered and Chaotic Motion
( \newcommand{\kernel}{\mathrm{null}\,}\)
Chapter 4.5 showed that motion in non-linear systems can exhibit both order and chaos. The transition between ordered motion and chaotic motion depends sensitively on both the initial conditions and the model parameters. It is surprisingly difficult to unambiguously distinguish between complicated ordered motion and chaotic motion. Moreover, the motion can fluctuate between order and chaos in an erratic manner depending on the initial conditions. The extremely sensitivity to initial conditions of the motion for non-linear systems, makes it essential to have quantitative measures that can characterize the degree of order, and interpret the complicated dynamical motion of systems. As an illustration, consider the harmonically-driven, linearly-damped, pendulum with Q=2, and driving force F(t)=FDsin˜ω˜t where ˜ω=23. Figure (4.5.5) shows the state-space plots for two driving amplitudes, FD=0.5 which leads to ordered motion, and FD=1.2 which leads to possible chaotic motion. It can be seen that for FD=0.5 the state-space diagram converges to a single attractor once the transient solution has died away. This is in contrast to the case for FD=1.2, where the state-space diagram does not converge to a single attractor, but exhibits possible chaotic motion. Three quantitative measures can be used to differentiate ordered motion from chaotic motion for this system; namely, the Lyapunov exponent, the bifurcation diagram, and the Poincaré section, as illustrated below.
Lyapunov Exponent
The Lyapunov exponent provides a quantitative and useful measure of the instability of trajectories, and how quickly nearby initial conditions diverge. It compares two identical systems that start with an infinitesimally small difference in the initial conditions in order to ascertain whether they converge to the same attractor at long times, corresponding to a stable system, or whether they diverge to very different attractors, characteristic of chaotic motion. If the initial separation between the trajectories in phase space at t=0 is |δZ0|, then to first order the time dependence of the difference can be assumed to depend exponentially on time. That is,
|δZ(t)|∼eλt|Z0|
where λ is the Lyapunov exponent. That is, the Lyapunov exponent is defined to be λ=limt→∞limδZ0→01tln|δZ(t)||Z0|
Systems for which the Lyapunov exponent λ<0 (negative), converge exponentially to the same attractor solution at long times since |δZ(t)|→0 for t→∞. By contrast, systems for which λ>0 (positive) diverge to completely different long-time solutions, that is, |δZ(t)|→∞ for t→∞. Even for infinitesimally small differences in the initial conditions, systems having a positive Lyapunov exponent diverge to different attractors, whereas when the Lyapunov exponent λ<0 they correspond to stable solutions.
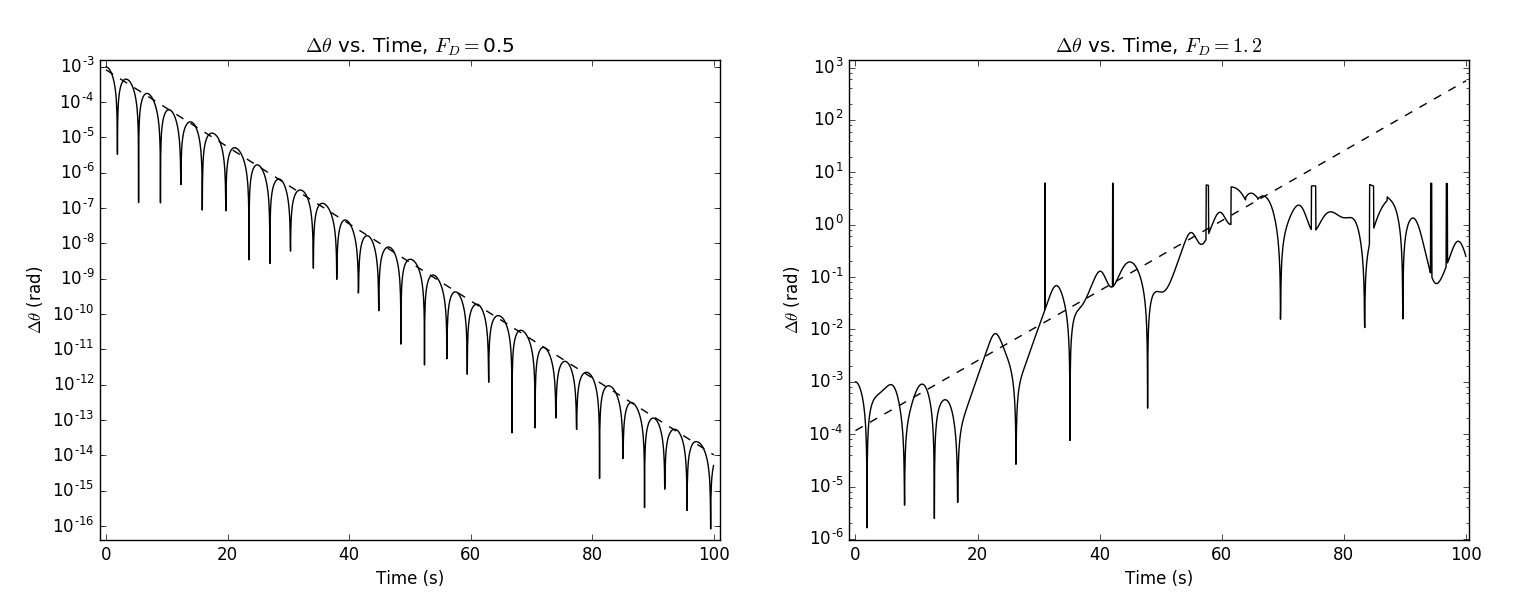
Figure 4.6.1 illustrates Lyapunov plots for the harmonically-driven, linearly-damped, plane pendulum, with the same conditions discussed in chapter 4.5. Note that for the small driving amplitude FD=0.5, the Lyapunov plot converges to ordered motion with an exponent λ=−0.251, whereas for FD=1.2, the plot diverges characteristic of chaotic motion with an exponent λ=0.1538. The Lyapunov exponent usually fluctuates widely at the local oscillator frequency, and thus the time average of the Lyapunov exponent must be taken over many periods of the oscillation to identify the general trend with time. Some systems near an order-to-chaos transition can exhibit positive Lyapunov exponents for short times, characteristic of chaos, and then converge to negative λ at longer time implying ordered motion. The Lyapunov exponents are used extensively to monitor the stability of the solutions for non-linear systems. For example the Lyapunov exponent is used to identify whether fluid flow is laminar or turbulent as discussed in chapter 16.8.
A dynamical system in n-dimensional phase space will have a set of n Lyapunov exponents {λ1,λ2,…,λn} associated with a set of attractors, the importance of which depend on the initial conditions. Typically one Lyapunov exponent dominates at one specific location in phase space, and thus it is usual to use the maximal Lyapunov exponent to identify chaos. The Lyapunov exponent is a very sensitive measure of the onset of chaos and provides an important test of the chaotic nature for the complicated motion exhibited by non-linear systems.
Bifurcation Diagram
The bifurcation diagram simplifies the presentation of the dynamical motion by sampling the status of the system once per period, synchronized to the driving frequency, for many sets of initial conditions. The results are presented graphically as a function of one parameter of the system in the bifurcation diagram. For example, the wildly different behavior in the driven damped plane pendulum is represented on a bifurcation diagram in Figure 4.6.2, which shows the observed angular velocity ω of the pendulum sampled once per drive cycle plotted versus drive strength. The bifurcation diagram is obtained by sampling either the angle θ, or angular velocity ω, once per drive cycle, that is, it represents the observables of the pendulum using a stroboscopic technique that samples the motion synchronous with the drive frequency. Bifurcation plots also can be created as a function of either the time ˜t, the damping factor Q, the normalized frequency ˜ω=ωω0, or the driving amplitude γ.

In the domain with drive strength γ<1.0663 there is one unique angle each drive cycle as illustrated by the bifurcation diagram. For slightly higher drive strength period-two bifurcation behavior results in two different angles per drive cycle. The Lyapunov exponent is negative for this region corresponding to ordered motion. The cascade of period doubling with increase in drive strength is readily apparent until chaos sets in at the critical drive strength γc when there is a random distribution of sampled angular velocities and the Lyapunov exponent becomes positive. Note that at γ=1.0845 there is a brief interval of period-6 motion followed by another region of chaos. Around γ=1.1 there is a region that is primarily chaotic which is reflected by chaotic values of the angular velocity on the bifurcation plot and large positive values of the Lyapunov exponent. The region around γ=1.12 exhibits period three motion and negative Lyapunov exponent corresponding to ordered motion. The 1.15<γ<1.25 region is mainly chaotic and has a large positive Lyapunov exponent. The region with 1.3<γ<1.4 is striking in that this corresponds to rolling motion with reemergence of period one and negative Lyapunov exponent. This period-1 motion is due to a continuous rolling motion of the plane pendulum as shown in figure (4.5.3) where it is seen that the average θ increases 2π per cycle, whereas the angular velocity ω exhibits a periodic motion. That is, on average the pendulum is rotating 2π per cycle. Above γ=1.4 the system start to exhibit period doubling followed by chaos reminiscent of the behavior seen at lower γ values.
These results show that the bifurcation diagram nicely illustrates the order to chaos transitions for the harmonically-driven, linearly-damped, pendulum. Several transitions between order and chaos are seen to occur. The apparent ordered and chaotic regimes are confirmed by the corresponding Lyapunov exponents which alternate between negative and positive values for the ordered and chaotic regions respectively.
Poincaré Section
State-space plots are very useful for characterizing periodic motion, but they become too dense for useful interpretation when the system approaches chaos as illustrated in Figure 4.6.2. Poincaré sections solve this difficulty by taking a stroboscopic sample once per cycle of the state-space diagram. That is, the point on the state space orbit is sampled once per drive frequency. For period-1 motion this corresponds to a single point (θ,ω). For period-2 motion this corresponds to two points etc. For chaotic systems the sequence of state-space sample points follow complicated trajectories. Figure 4.6.3 shows the Poincaré sections for the corresponding state space diagram shown in figure (4.5.5) for cycles 10 to 6000. Note the complicated curves do not cross or repeat. Enlargements of any part of this plot will show increasingly dense parallel trajectories, called fractals, that indicates the complexity of the chaotic cyclic motion. That is, zooming in on a small section of this Poincaré plot shows many closely parallel trajectories. The fractal attractors are surprisingly robust to large differences in initial conditions. Poincaré sections are a sensitive probe of periodic motion for systems where periodic motion is not readily apparent.
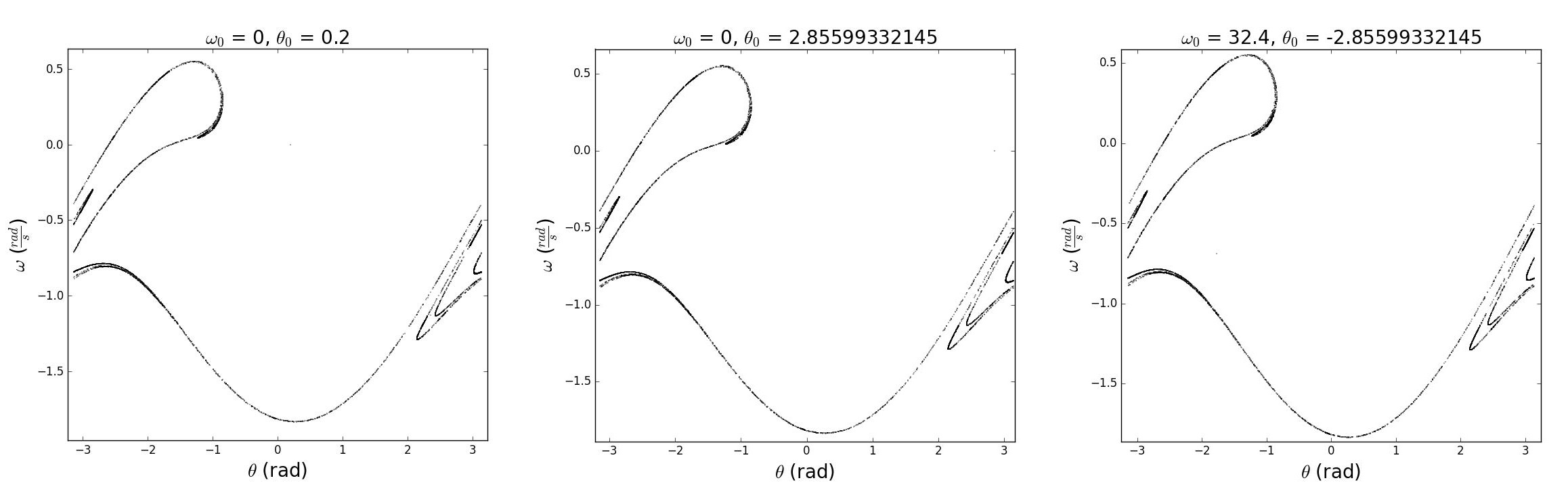
In summary, the behavior of the well-known, harmonically-driven, linearly-damped, plane pendulum becomes remarkably complicated at large driving amplitudes where non-linear effects dominate. That is, when the restoring force is non-linear. The system exhibits bifurcation where it can evolve to multiple attractors that depend sensitively on the initial conditions. The system exhibits both oscillatory, and rolling, solutions depending on the amplitude of the motion. The system exhibits domains of simple ordered motion separated by domains of very complicated ordered motion as well as chaotic regions. The transitions between these dramatically different modes of motion are extremely sensitive to the amplitude and phase of the driver. Eventually the motion becomes completely chaotic. The Lyapunov exponent, bifurcation diagram, and Poincaré section plots, are sensitive measures of the order of the motion. These three sensitive measures of order and chaos are used extensively in many fields in classical mechanics. Considerable computing capabilities are required to elucidate the complicated motion involved in non-linear systems. Examples include laminar and turbulent flow in fluid dynamics and weather forecasting of hurricanes, where the motion can span a wide dynamic range in dimensions from 10−5 to 104 m.


