4.7: Wave Propagation for Non-linear Systems
( \newcommand{\kernel}{\mathrm{null}\,}\)
Phase, group, and signal velocities
Chapter 3 discussed the wave equation and solutions for linear systems. It was shown that, for linear systems, the wave motion obeys superposition and exhibits dispersion, that is, a frequency-dependent phase velocity, and, in some cases, attenuation. Nonlinear systems introduce intriguing new wave phenomena. For example for nonlinear systems, second, and higher terms must be included in the Taylor expansion given in equation (4.2.2). These second and higher order terms result in the group velocity being a function of ω, that is, group velocity dispersion occurs which leads to the shape of the envelope of the wave packet being time dependent. As a consequence the group velocity in the wave packet is not well defined, and does not equal the signal velocity of the wave packet or the phase velocity of the wavelets. Nonlinear optical systems have been studied experimentally where vgroup<<c, which is called slow light, while other systems have vgroup>c which is called superluminal light. The ability to control the velocity of light in such optical systems is of considerable current interest since it has signal transmission applications.
The dispersion relation for a nonlinear system can be expressed as a Taylor expansion of the form
k=k0+(∂k∂ω)ω=ω0(ω−ω0)+12(∂2k∂ω2)ω=ω0(ω−ω0)2+..
where ω is used as the independent variable since it is invariant to phase transitions of the system. Note that the factor for the first derivative term is the reciprocal of the group velocity
(∂k∂ω)ω=ω0≡1vgroup
while the factor for the second derivative term is
(∂2k∂ω2)ω=ω0=∂∂ω[1vgroup(ω)]ω=ω0=(−1v2group∂vgroup∂ω)ω=ω0
which gives the velocity dispersion for the system.
Since
k=ωvphase
then
∂k∂ω≡1vgroup=1vphase+ω∂1vphase∂ω
The inverse velocities for electromagnetic waves are best represented in terms of the corresponding refractive indices n, where
n≡cvphase
and the group refractive index
ngroup≡cvgroup
Then Equation ??? can be written in the more convenient form ngroup=n+ω∂n∂ω
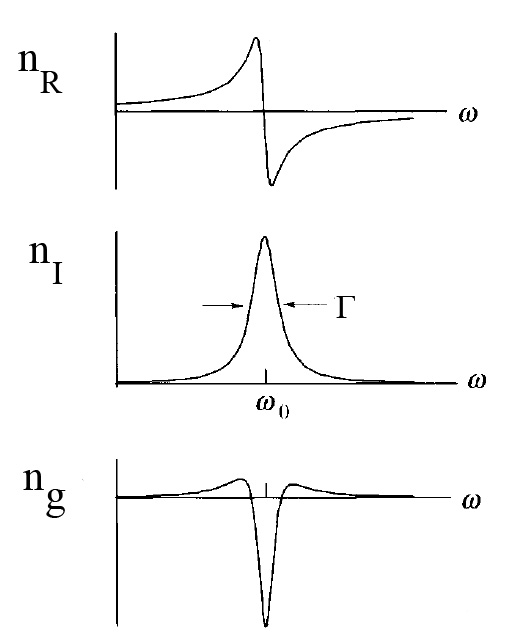
Wave propagation for an optical system that is subject to a single resonance gives one example of nonlinear frequency response that has applications to optics.
Figure 4.7.1 shows that the real nR and imaginary nI parts of the phase refractive index exhibit the characteristic resonance frequency dependence of the sinusoidally-driven, linear oscillator that was discussed in chapter 3.6 and as illustrated in figure (3.6.4). Figure 4.7.1 also shows the group refractive index ngroup computed using Equation ???.
Note that at resonance, ngroup is reduced below the non-resonant value which corresponds to superluminal (fast) light, whereas in the wings of the resonance ngroup is larger than the non-resonant value corresponding to slow light. Thus the nonlinear dependence of the refractive index n on angular frequency ω leads to fast or slow group velocities for isolated wave packets. Velocities of light as slow as 17 m/sec have been observed. Experimentally the energy absorption that occurs on resonance makes it difficult to observe the superluminal electromagnetic wave at resonance.
Note that Sommerfeld and Brillouin showed that even though the group velocity may exceed c, the signal velocity, which marks the arrival of the leading edge of the optical pulse, does not exceed c, the velocity of light in vacuum, as was postulated by Einstein.
Soliton wave propagation
The soliton is a fascinating and very special wave propagation phenomenon that occurs for certain non-linear systems. The soliton is a self-reinforcing solitary localized wave packet that maintains its shape while travelling long distances at a constant speed. Solitons are caused by a cancellation of phase modulation resulting from non-linear velocity dependence, and the group velocity dispersive effects in a medium. Solitons arise as solutions of a widespread class of weakly-nonlinear dispersive partial differential equations describing many physical systems. Figure 4.7.2 shows a soliton comprising a solitary water wave approaching the coast of Hawaii. While the soliton in Fig. 4.7.2 may appear like a normal wave, it is unique in that there are no other waves accompanying it. This wave was probably created far away from the shore when a normal wave was modulated by a geometrical change in the ocean depth, such as the rising sea floor, which forced it into the appropriate shape for a soliton. The wave then was able to travel to the coast intact, despite the apparently placid nature of the ocean near the beach. Solitons are notable in that they interact with each other in ways very different from normal waves. Normal waves are known for their complicated interference patterns that depend on the frequency and wavelength of the waves. Solitons, can pass right through each other without being a affected at all. This makes solitons very appealing to scientists because soliton waves are more sturdy than normal waves, and can therefore be used to transmit information in ways that are distinctly different than for normal wave motion. For example, optical solitons are used in optical fibers made of a dispersive, nonlinear optical medium, to transmit optical pulses with an invariant shape.

Solitons were first observed in 1834 by John Scott Russell (1808−1882). Russell was an engineer conducting experiments to increase the efficiency of canal boats. His experimental and theoretical investigations allowed him to recreate the phenomenon in wave tanks. Through his extensive studies, Scott Russell noticed that soliton propagation exhibited the following properties:
- The waves are stable and hold their shape for long periods of time.
- The waves can travel over long distances at uniform speed.
- The speed of propagation of the wave depends on the size of the wave, with larger waves traveling faster than smaller waves.
- The waves maintained their shape when they collided - seemingly passing right through each other.
Scott Russell’s work was met with scepticism by the scientific community. The problem with the Wave of Translation was that it was an effect that depended on nonlinear effects, whereas previously existing theories of hydrodynamics (such as those of Newton and Bernoulli) only dealt with linear systems. George Biddell Airy, and George Gabriel Stokes, published papers attacking Scott Russell’s observations because the observations could not be explained by their theories of wave propagation in water. Regardless, Scott Russell was convinced of the prime importance of the Wave of Translation, and history proved that he was correct. Scott Russell went on to develop the "wave line" system of hull construction that revolutionized nineteenth century naval architecture, along with a number of other great accomplishments leading him to fame and prominence. Despite all of the success in his career, he continued throughout his life to pursue his studies of the Wave of Translation.
In 1895 Korteweg and de Vries developed a wave equation for surface waves for shallow water.
∂ϕ∂t+∂3ϕ∂x3+6ϕ∂ϕ∂x=0 A solution of this equation has the characteristics of a solitary wave with fixed shape. It is given by substituting the form ϕ(x,t)=f(x−vt) into the Korteweg-de Vries equation which gives
−v∂f∂x+∂3f∂x3+6f∂f∂x=0 Integrating with respect to x gives
3f2+d2fdx3−cf=C
where C is a constant of integration. This non-linear equation has a solution
ϕ(x,t)=12csech2[√v2(x−vt−a)]
where a is a constant. Equation ??? is the equation of a solitary wave moving in the +x direction at a velocity v.
Soliton behavior is observed in phenomena such as tsunamis, tidal bores that occur for some rivers, signals in optical fibres, plasmas, atmospheric waves, vortex filaments, superconductivity, and gravitational fields having cylindrical symmetry. Much work has been done on solitons for fibre optics applications. The soliton’s inherent stability make long-distance transmission possible without the use of repeaters, and could potentially double the transmission capacity.
Before the discovery of solitons, mathematicians were under the impression that nonlinear partial differential equations could not be solved exactly. However, solitons led to the recognition that there are non-linear systems that can be solved analytically. This discovery has prompted much investigation into these so-called "integrable systems." Such systems are rare, as most non-linear differential equations admit chaotic behavior with no explicit solutions. Integrable systems nevertheless lead to very interesting mathematics ranging from differential geometry and complex analysis to quantum field theory and fluid dynamics.
Many of the fundamental equations in physics (Maxwell’s, Schrödinger’s) are linear equations. However, physicists have begun to recognize many areas of physics in which nonlinearity can result in qualitatively new phenomenon which cannot be constructed via perturbation theory starting from linearized equations. These include phenomena in magnetohydrodynamics, meteorology, oceanography, condensed matter physics, nonlinear optics, and elementary particle physics. For example, the European space mission Cluster detected a soliton-like electrical disturbances that travelled through the ionized gas surrounding the Earth starting about 50,000 kilometers from Earth and travelling towards the planet at about 8 km/s. It is thought that this soliton was generated by turbulence in the magnetosphere.
Efforts to understand the nonlinearity of solitons has led to much research in many areas of physics. In the context of solitons, their particle-like behavior (in that they are localized and preserved under collisions) leads to a number of experimental and theoretical applications. The technique known as bosonization allows viewing particles, such as electrons and positrons, as solitons in appropriate field equations. There are numerous macroscopic phenomena, such as internal waves on the ocean, spontaneous transparency, and the behavior of light in fiber optic cable, that are now understood in terms of solitons. These phenomena are being applied to modern technology.


