6.9: Applications involving Non-holonomic Constraints
- Page ID
- 14061
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)In general, non-holonomic constraints can be handled by use of generalized forces \(Q_{j}^{EXC}\) in the Lagrange-Euler equations \((6.5.12)\). The following examples, \(\PageIndex{1}-\PageIndex{4}\), involve one-sided constraints which exhibit holonomic behavior for restricted ranges of the constraint surface in coordinate space, and this range is case specific. When the forces of constraint press the object against the constraint surface, then the system is holonomic, but the holonomic range of coordinate space is limited to situations where the constraint forces are positive. When the constraint force is negative, the object flies free from the constraint surface. In addition, when the frictional force \(F>N\mu _{static}\) where \(\mu _{static}\) is the static coefficient of friction, then the object slides negating any rolling constraint that assumes static friction.
Example \(\PageIndex{1}\): Mass sliding on a frictionless spherical shell
Consider a mass starts from rest at the top of a frictionless fixed spherical shell of radius \(R\). The questions are what is the force of constraint and determine the angle \(\theta\) at which the mass leaves the surface of the spherical shell. The coordinates \(r,\theta\) shown are the obvious generalized coordinates to use.
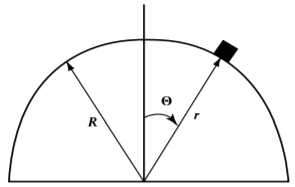
The constraint will not apply if the force of constraint does not hold the mass against the surface of the spherical shell, that is, it is only holonomic in a restricted domain.
\[L= \frac{1}{2}m\left( \dot{r}^{2}+r^{2}\dot{\theta}^{2}\right) -mgr\cos \theta \nonumber\]
This Lagrangian is applicable irrespective of whether the constraint is obeyed, where the constraint is given by \[g(r,\theta )=r-R=0\nonumber\]
For the restricted domain where this system is holonomic, it can be solved using generalized coordinates, generalized forces, Lagrange multipliers, or Newtonian mechanics as illustrated below.
Minimal generalized coordinates:
The minimal number of generalized coordinates reduces the system to one coordinate \(\theta\), which does not determine the constraint force that is needed to know if the constraint applies. Thus this approach is not useful for solving this partially-holonomic system.
Generalized forces:
\[F=Q_{r}=mg(3\cos \theta -2)\nonumber\]
Note that \(F=Q_{r}=0\) when \(\cos \theta =\frac{2}{3}\), that is \(\theta =48.2^{o}.\)
Lagrange multipliers:
\[m\ddot{r}+mg\cos \theta -mr\dot{\theta}^{2}=\lambda \tag{a}\]
The Lagrange equation for \(\theta\) gives \(\Delta _{\theta }L=\lambda \frac{\partial g}{\partial \theta }=0\) since \(\frac{\partial g}{\partial \theta }=0.\) Thus \[mr^{2}\ddot{\theta}-mgr\sin \theta +2mr\dot{r}\dot{\theta}=0 \tag{b} \label{b2}\]
\[\dot{\theta}^{2}=\frac{2g}{R}\left( 1-\cos \theta \right) \tag{d} \label{d2}\]
assuming that \(\dot{\theta}=0\) at \(\theta =0.\)
\[F=\lambda =mg(3\cos \theta -2)\nonumber\]
Note that \(\lambda =0\) when \(\cos \theta =\frac{2}{3}\), that is \(\theta =48.2^{o}.\)
Both of the above methods give identical results and give that the force of constraint is negative when \(\theta >48.2^{o}.\) Assuming that the surface cannot hold the mass against the surface, then the mass will fly off the spherical shell when \(\theta >48.2^{o}\) and the system reduces to an unconstrained object falling freely in a uniform gravitational field, which is holonomic, that is \(Q_{r}=\lambda =0.\) Then the equations of motion \(\left( a\right)\) and \((b)\) reduce to \[\begin{align} m\ddot{r}+mg\cos \theta -mr\dot{\theta}^{2} &=&0 \tag{e} \\ mr^{2}\ddot{\theta}-mgr\sin \theta +2mr\dot{r}\dot{\theta} &=&0 \tag{f}\end{align}\]
Energy conservation:
\[\frac{v^{2}}{R}=2g[1-\cos \theta ]=g\cos \theta\nonumber\]
This occurs when \(\cos \theta =\frac{2}{3}\). This is an unusual case where the Newtonian approach is the simplest.
Example \(\PageIndex{2}\): Rolling solid sphere on a spherical shell
This is a similar problem to the prior one with the added complication of rolling which is assumed to move in a vertical plane making it holonomic. Here we would like to determine the forces of constraint to see when the solid sphere flies off the spherical shell and when the friction is insufficient to stop the rolling sphere from slipping.
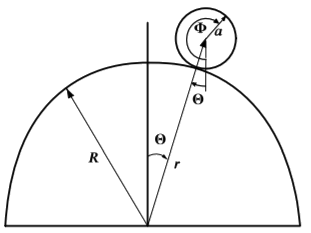
The best generalized coordinates are the distance of the center of the sphere from the center of the spherical shell, \(r,\theta\) and \(\phi .\) It is important to note that \(\phi\) is measured with respect to the vertical, not the time-dependent vector \(\mathbf{r}\). That is, the direction of the radius \(r\) is \(\theta\) which is time dependent and thus is not a useful reference to use to define the angle \(\phi\). Let us assume that the sphere is uniform with a moment of inertia of \(I= \frac{2}{5}ma^{2}.\) If the tangential frictional force \(F\) is less than the limiting value \(N\mu _{statics}\), with \(N>0,\) then the sphere will roll without slipping on the surface of the cylinder and both constraints apply. Under these conditions the system is holonomic and the solution is solved using Lagrange multipliers and the equations of constraint are the following:
- The center of the sphere follows the surface of the cylinder \[g_{1}=r-R-a=0\nonumber\]
- The sphere rolls without slipping \[g_{2}=a\left( \phi -\theta \right) -R\theta =0\nonumber\]
The kinetic energy is \(T=\frac{1}{2}m\left( \dot{r}^{2}+r^{2}\dot{ \theta}^{2}\right) +\frac{1}{2}I\dot{\phi}^{2}\) and the potential energy is \(U=mgr\cos \theta .\) Thus the Lagrangian is \[L=\frac{1}{2}m\left( \dot{r}^{2}+r^{2}\dot{\theta}^{2}\right) +\frac{1}{2}I \dot{\phi}^{2}-mgr\cos \theta\nonumber\]
\[mr^{2}\ddot{\theta}+2mr\dot{r}\dot{\theta}-mgr\sin \theta =-\lambda _{2}\left( R+a\right) \tag{b} \label{b3}\]
\(\Lambda _{\phi }L\) gives \[I\ddot{\phi}=a\lambda _{2} \tag{c}\]
\[\cos \theta =\frac{10}{17}\nonumber\]
For larger angles \(\lambda _{1}\) is negative implying that the solid sphere will fly off the surface of the spherical shell.
The sphere will leave the surface of the cylinder when \(\cos \theta =\frac{10}{17}\) that is, \(\theta =53.97^{o}.\) This is a significantly larger angle than obtained for the similar problem where the mass is sliding on a frictionless cylinder because the energy stored in rotation implies that the linear velocity of the mass is lower at a given angle \(\theta\) for the case of a rolling sphere.
\[F_{f}=-\lambda _{2}\nonumber\]
It is in the negative direction because of the direction chosen for \(\phi .\) The required coefficient of friction \(\mu\) is given by the ratio of the frictional force to the normal force, that is \[\mu =\frac{\lambda _{2}}{\lambda _{1}}=\frac{2\sin \theta }{\left[ 17\cos \theta -10\right] }\nonumber\]
For \(\mu =1\) the disk starts to slip when \(\theta =47.54^{0}.\) Note that the sphere starts slipping before it flies off the cylinder since a normal force is required to support a frictional force and the difference depends on the coefficient of friction. The no-slipping constraint is not satisfied once the sphere starts slipping and the frictional force should equal \(\mu _{kinetic}\lambda _{1}.\) Thus for the angles beyond \(47.54^{o}\) the problem needs to be solved with the rolling constraint changed to a sliding non-conservative frictional force. This is best handled by including the frictional force and normal forces as generalized forces. Fortunately this will be a small correction. The friction will slightly change the exact angle at which the normal force becomes zero and the system transitions to free motion of the sphere in a gravitational field.
Example \(\PageIndex{3}\): Solid sphere rolling plus slipping on a spherical shell
\[F=N\mu _{sliding}\nonumber\]
when \(N\) is positive.
\[\frac{d}{dt}\frac{\partial L}{\partial \dot{r}}-\frac{\partial L}{\partial r} =Q_{r}=N\nonumber\]
which gives \[m\ddot{r}+mg\cos \theta -mr\dot{\theta}^{2}=N\nonumber\]
\[mr^{2}\ddot{\theta}+2mr\dot{r}\dot{\theta}-mgr\sin \theta =-F\left( R+a\right)\nonumber\]
Similarly \(\Lambda _{\phi }L=Q_{\phi }=aF\) gives \[I\ddot{\phi}=aF\nonumber\]
These can be solved by substituting the relation \(F=N\mu _{sliding}\). The sphere flies off the spherical shell when \(N\leq 0\) leading to free motion discussed in example \((7.7.2)\). The problem of a solid uniform sphere rolling inside a hollow sphere can be solved the same way.
Example \(\PageIndex{4}\): Small body held by friction on the periphery of a rolling wheel
Assume that a small body of mass \(m\) is balanced on a rolling wheel of mass \(M\) and radius \(R\) as shown in the figure. The wheel rolls in a vertical plane without slipping on a horizontal surface. This example illustrates that it is possible to use simultaneously a mixture of holonomic constraints, partially-holonomic constraints, and generalized forces.3
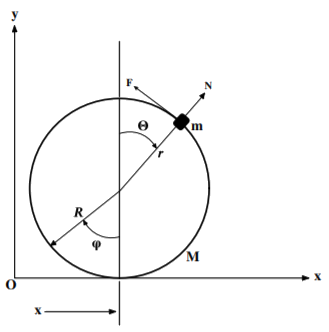
Assume that at \(t=0\) the wheel touches the floor at \(x=y=0\) with the mass perched at the top of the wheel at \(x=0\). Let the frictional force acting on the mass \(m\) be \(F\) and the reaction force of the periphery of the wheel on the mass be \(N\). Let \(\dot{\varphi}\) be the angular velocity of the wheel, and \(\dot{x}\) the horizontal velocity of the center of the wheel. The polar coordinates \(r,\theta\) of the mass \(m\) are taken with \(r\) measured from the center of the wheel with \(\theta\) measured with respect to the vertical. Thus the cartesian coordinates of the small mass \(m\) are \((x+r\sin \theta ,R+r\cos \theta )\) with respect to the origin at \(x=y=0\).
\[U=+mg\left( R+r\cos \theta \right)\nonumber\]
Thus the Lagrangian is \[L=\frac{1}{2}\left( M+m\right) \dot{x}^{2}+\frac{1}{2}I\dot{\varphi}^{2}+ \frac{1}{2}m\left[ r^{2}\dot{\theta}^{2}+2r\dot{x}\dot{\theta}\cos \theta +2 \dot{x}\dot{r}\sin \theta +\dot{r}^{2}\right] -mg\left( R+r\cos \theta \right)\nonumber\]
The equations of constraints are:
1) The wheel rolls without slipping on the ground plane leading to a holonomic constraint: \[g_{1}=x-R\varphi =\dot{x}-R\dot{\varphi}=0\]
2) The mass \(m\) is touching the periphery of the wheel, that is, the normal force \(N>0.\) This is a one-sided restricted holonomic constraint. \[g_{2}=R-r=0\nonumber\]
3) The mass \(m\) does not slip on the wheel if the frictional force \(F<\) \(N\mu _{static}\). When this restricted holonomic constraint is satisfied, then \[g_{3}=\dot{\theta}-\dot{\varphi}=0\]
The rolling constraint is holonomic, and can be accounted for using one Lagrange multiplier \(\lambda _{x}\) plus the differential constraint equations
\[m\ddot{x}\sin \theta +mR\dot{\theta}^{2}-mg\cos \theta +N=0\nonumber\]
This last equation can be derived by Newtonian mechanics from consideration of the forces acting.
The above equations of motion can be used to calculate the motion for the following conditions.
a) Mass not slipping:
This occurs if \(\mu =\frac{F}{N}\leq \mu _{static}\) which also implies that \(N>0,\) That is a situation where the system is holonomic with \(r=R,\) \(\dot{x}=R\dot{\varphi},\) \(\dot{ \theta}=\dot{\varphi}\) which can be solved using the generalized coordinate approach with only one independent coordinate which can be taken to be \(\theta\).
b) Mass slipping:
Here the no-slip constraint is violated and thus one has to explicitly include the generalized forces \(Q_{r},Q_{\varphi },Q_{\theta }\) and assume that sliding friction is given by \(F=N\mu _{sliding}.\)
c) Reaction force \(N\) is negative:
Here the mass is not subject to any constraints and it is in free fall.
The above example illustrates the flexibility provided by Lagrangian mechanics that allows simultaneous use of Lagrange multipliers, generalized forces, and scalar potential to handle combinations of several holonomic and nonholonomic constraints for a complicated problem.
3This problem is solved in detail in example 3.19 of "Classical Mechanics and Relativity". by Muller-Kirsten \(\left[ Mu06\right] \).


