14.6: Convection
- Page ID
- 1591
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Learning Objectives
By the end of this section, you will be able to:
- Discuss the method of heat transfer by convection.
Convection is driven by large-scale flow of matter. In the case of Earth, the atmospheric circulation is caused by the flow of hot air from the tropics to the poles, and the flow of cold air from the poles toward the tropics. (Note that Earth’s rotation causes the observed easterly flow of air in the northern hemisphere). Car engines are kept cool by the flow of water in the cooling system, with the water pump maintaining a flow of cool water to the pistons. The circulatory system is used the body: when the body overheats, the blood vessels in the skin expand (dilate), which increases the blood flow to the skin where it can be cooled by sweating. These vessels become smaller when it is cold outside and larger when it is hot (so more fluid flows, and more energy is transferred).
The body also loses a significant fraction of its heat through the breathing process.
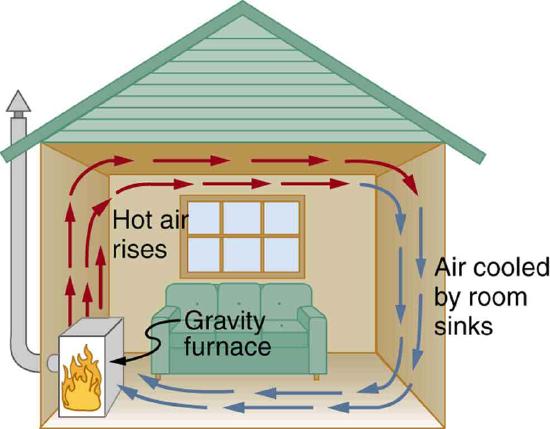
While convection is usually more complicated than conduction, we can describe convection and do some straightforward, realistic calculations of its effects. Natural convection is driven by buoyant forces: hot air rises because density decreases as temperature increases. The house in Figure \(\PageIndex{1}\) is kept warm in this manner, as is the pot of water on the stove in Figure \(\PageIndex{2}\). Ocean currents and large-scale atmospheric circulation transfer energy from one part of the globe to another. Both are examples of natural convection.
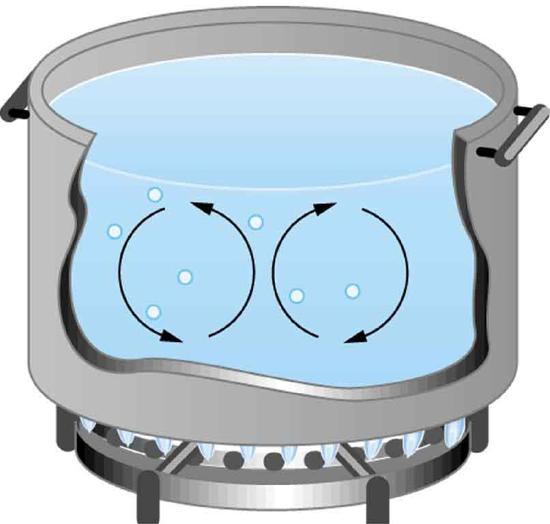
Take-Home Experiment: Convection Rolls in a Heated Pan
Take two small pots of water and use an eye dropper to place a drop of food coloring near the bottom of each. Leave one on a bench top and heat the other over a stovetop. Watch how the color spreads and how long it takes the color to reach the top. Watch how convective loops form.
Example \(\PageIndex{1}\): Calculating Heat Transfer by Convection: Convection of Air Through the Walls of a House
Most houses are not airtight: air goes in and out around doors and windows, through cracks and crevices, following wiring to switches and outlets, and so on. The air in a typical house is completely replaced in less than an hour. Suppose that a moderately-sized house has inside dimensions \(12.0m \times 18.0 m \times 3.00 m\) high, and that all air is replaced in 30.0 min. Calculate the heat transfer per unit time in watts needed to warm the incoming cold air by \(10.0^oC\) thus replacing the heat transferred by convection alone.
Strategy
Heat is used to raise the temperature of air so that \(Q = mc\Delta T\). The rate of heat transfer is then \(Q/t\), where \(t\) is the time for air turnover. We are given that \(\Delta T\) is \(10.0^oC\), but we must still find values for the mass of air and its specific heat before we can calculate \(Q\). The specific heat of air is a weighted average of the specific heats of nitrogen and oxygen, which gives \(c = c_p \approx 1000 \, J/kg \cdot ^oC\) from the table (note that the specific heat at constant pressure must be used for this process).
Solution
- Determine the mass of air from its density and the given volume of the house. The density is given from the density \(\rho\) and the volume \[m = \rho V = (1.29 \, kg/m^3)912.0 \, m \times 18.0 \, m \times 3.00 \, m) = 836 \, kg\]
- Calculate the heat transferred from the change in air temperature \(Q = mc \Delta T\) so that \[Q = (836 \, kg)(1000 \, J/kg \cdot^oC)(10.0^oC) = 8.36 \times 10^6 \, J.\]
- Calculate the heat transfer from the heat \(Q\) and the turnover time \(t\). Since air is turned over in \(t = 0.500 \, h = 1800 \, s\), the heat transferred per unit time is \[\dfrac{Q}{t} = \dfrac{8.36 \times 10^6 \, J}{1800 \, s} = 4.64 \, kW.\]
Discussion
This rate of heat transfer is equal to the power consumed by about forty-six 100-W light bulbs. Newly constructed homes are designed for a turnover time of 2 hours or more, rather than 30 minutes for the house of this example. Weather stripping, caulking, and improved window seals are commonly employed. More extreme measures are sometimes taken in very cold (or hot) climates to achieve a tight standard of more than 6 hours for one air turnover. Still longer turnover times are unhealthy, because a minimum amount of fresh air is necessary to supply oxygen for breathing and to dilute household pollutants. The term used for the process by which outside air leaks into the house from cracks around windows, doors, and the foundation is called “air infiltration.”
A cold wind is much more chilling than still cold air, because convection combines with conduction in the body to increase the rate at which energy is transferred away from the body. The table below gives approximate wind-chill factors, which are the temperatures of still air that produce the same rate of cooling as air of a given temperature and speed. Wind-chill factors are a dramatic reminder of convection’s ability to transfer heat faster than conduction. For example, a 15.0 m/s wind at \(0^oC\) has the chilling equivalent of still air at about \(-18^oC\).
Moving air temperature Wind speed (m/s)
| \(^oC\) | 2 | 5 | 10 | 15 | 20 |
|---|---|---|---|---|---|
| 5 | 3 | -1 | -8 | -10 | -12 |
| 2 | 0 | -7 | -12 | -16 | -18 |
| 0 | -2 | -9 | -15 | -18 | -20 |
| -5 | -7 | -15 | -22 | -26 | -29 |
| -10 | -12 | -21 | -29 | -34 | -36 |
| -20 | -23 | -34 | -44 | -50 | -52 |
| -40 | -44 | -59 | -73 | -82 | -84 |
Although air can transfer heat rapidly by convection, it is a poor conductor and thus a good insulator. The amount of available space for airflow determines whether air acts as an insulator or conductor. The space between the inside and outside walls of a house, for example, is about 9 cm (3.5 in) —large enough for convection to work effectively. The addition of wall insulation prevents airflow, so heat loss (or gain) is decreased. Similarly, the gap between the two panes of a double-paned window is about 1 cm, which prevents convection and takes advantage of air’s low conductivity to prevent greater loss. Fur, fiber, and fiberglass also take advantage of the low conductivity of air by trapping it in spaces too small to support convection, as shown in the figure. Fur and feathers are lightweight and thus ideal for the protection of animals.
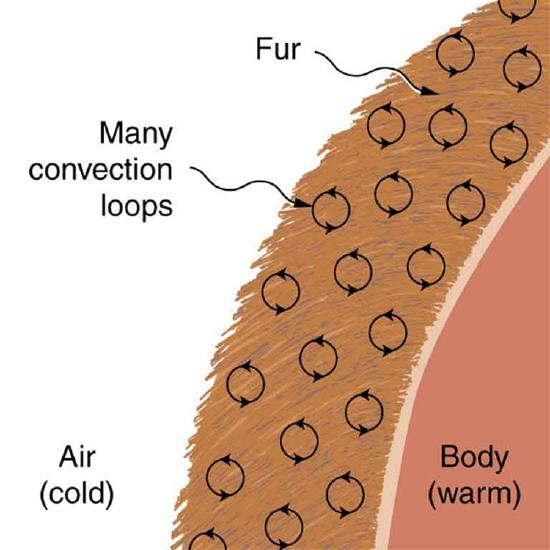
Some interesting phenomena happen when convection is accompanied by a phase change. It allows us to cool off by sweating, even if the temperature of the surrounding air exceeds body temperature. Heat from the skin is required for sweat to evaporate from the skin, but without air flow, the air becomes saturated and evaporation stops. Air flow caused by convection replaces the saturated air by dry air and evaporation continues.
Example \(\PageIndex{2}\): Calculate the Flow of Mass during Convection: Sweat-Heat Transfer away from the Body
The average person produces heat at the rate of about 120 W when at rest. At what rate must water evaporate from the body to get rid of all this energy? (This evaporation might occur when a person is sitting in the shade and surrounding temperatures are the same as skin temperature, eliminating heat transfer by other methods.)
Strategy
Energy is needed for a phase change \((Q = mL_v)\). Thus, the energy loss per unit time is \[\dfrac{Q}{t} = \dfrac{mL_v}{t} = 120 \, W = 120 \, J/s.\]
We divide both sides of the equation by \(L_v\) to find that the mass evaporated per unit time is \[\dfrac{m}{t} = \dfrac{120 \, J/s}{L_v}.\]
Solution
(1) Insert the value of the latent heat from [link], \(L_v = 2430 \, kJ/kg = 2430 \, J/g\). This yields \[\dfrac{m}{t} = \dfrac{120 \, J/s}{2430 \, J/g} = 0.0494 \, g/s = 2.96 \, g/min.\]
Discussion
Evaporating about 3 g/min seems reasonable. This would be about 180 g (about 7 oz) per hour. If the air is very dry, the sweat may evaporate without even being noticed. A significant amount of evaporation also takes place in the lungs and breathing passages.
Another important example of the combination of phase change and convection occurs when water evaporates from the oceans. Heat is removed from the ocean when water evaporates. If the water vapor condenses in liquid droplets as clouds form, heat is released in the atmosphere. Thus, there is an overall transfer of heat from the ocean to the atmosphere. This process is the driving power behind thunderheads, those great cumulus clouds that rise as much as 20.0 km into the stratosphere. Water vapor carried in by convection condenses, releasing tremendous amounts of energy. This energy causes the air to expand and rise, where it is colder. More condensation occurs in these colder regions, which in turn drives the cloud even higher. Such a mechanism is called positive feedback, since the process reinforces and accelerates itself. These systems sometimes produce violent storms, with lightning and hail, and constitute the mechanism driving hurricanes.



The movement of icebergs is another example of convection accompanied by a phase change. Suppose an iceberg drifts from Greenland into warmer Atlantic waters. Heat is removed from the warm ocean water when the ice melts and heat is released to the land mass when the iceberg forms on Greenland.
Exercise \(\PageIndex{1}\)
Explain why using a fan in the summer feels refreshing!
- Answer
-
Using a fan increases the flow of air: warm air near your body is replaced by cooler air from elsewhere. Convection increases the rate of heat transfer so that moving air “feels” cooler than still air.
Summary
- Convection is heat transfer by the macroscopic movement of mass. Convection can be natural or forced and generally transfers thermal energy faster than conduction. The table gives wind-chill factors, indicating that moving air has the same chilling effect of much colder stationary air. Convection that occurs along with a phase change can transfer energy from cold regions to warm ones.


