29.4: Photon Momentum
( \newcommand{\kernel}{\mathrm{null}\,}\)
Learning Objectives
By the end of this section, you will be able to:
- Relate the linear momentum of a photon to its energy or wavelength, and apply linear momentum conservation to simple processes involving the emission, absorption, or reflection of photons.
- Account qualitatively for the increase of photon wavelength that is observed, and explain the significance of the Compton wavelength.
Measuring Photon Momentum
The quantum of EM radiation we call a photon has properties analogous to those of particles we can see, such as grains of sand. A photon interacts as a unit in collisions or when absorbed, rather than as an extensive wave. Massive quanta, like electrons, also act like macroscopic particles—something we expect, because they are the smallest units of matter. Particles carry momentum as well as energy. Despite photons having no mass, there has long been evidence that EM radiation carries momentum. (Maxwell and others who studied EM waves predicted that they would carry momentum.) It is now a well-established fact that photons do have momentum. In fact, photon momentum is suggested by the photoelectric effect, where photons knock electrons out of a substance. Figure 29.4.1 shows macroscopic evidence of photon momentum.
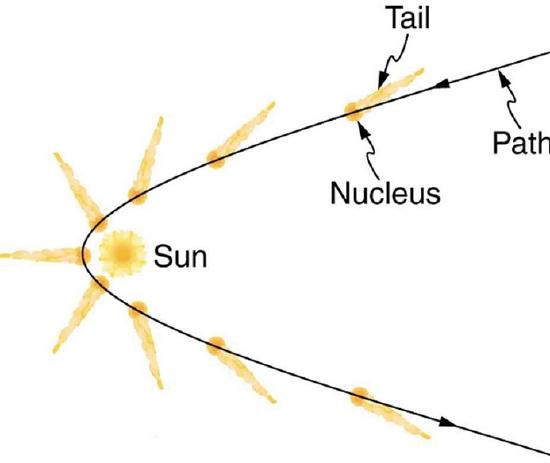

Figure 29.4.1 shows a comet with two prominent tails. What most people do not know about the tails is that they always point away from the Sun rather than trailing behind the comet (like the tail of Bo Peep’s sheep). Comet tails are composed of gases and dust evaporated from the body of the comet and ionized gas. The dust particles recoil away from the Sun when photons scatter from them. Evidently, photons carry momentum in the direction of their motion (away from the Sun), and some of this momentum is transferred to dust particles in collisions. Gas atoms and molecules in the blue tail are most affected by other particles of radiation, such as protons and electrons emanating from the Sun, rather than by the momentum of photons.
Connections: Conservation of Momentum
Not only is momentum conserved in all realms of physics, but all types of particles are found to have momentum. We expect particles with mass to have momentum, but now we see that massless particles including photons also carry momentum.
Momentum is conserved in quantum mechanics just as it is in relativity and classical physics. Some of the earliest direct experimental evidence of this came from scattering of x-ray photons by electrons in substances, named Compton scattering after the American physicist Arthur H. Compton (1892–1962). Around 1923, Compton observed that x rays scattered from materials had a decreased energy and correctly analyzed this as being due to the scattering of photons from electrons. This phenomenon could be handled as a collision between two particles—a photon and an electron at rest in the material. Energy and momentum are conserved in the collision (Figure 29.4.2) He won a Nobel Prize in 1929 for the discovery of this scattering, now called the Compton effect, because it helped prove that photon momentum is given by
p=hλ,
where h is Planck's constant and λ is the photon wavelength. (Note that relativistic momentum given as p=γmu is valid only for particles having mass.)
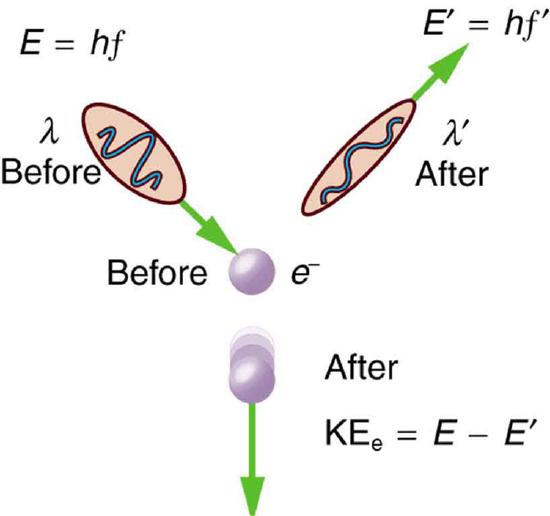
We can see that photon momentum is small, since p=h/λ and h is very small. It is for this reason that we do not ordinarily observe photon momentum. Our mirrors do not recoil when light reflects from them (except perhaps in cartoons). Compton saw the effects of photon momentum because he was observing x rays, which have a small wavelength and a relatively large momentum, interacting with the lightest of particles, the electron.
Example 29.4.1: Electron and Photon Momentum Compared
- Calculate the momentum of a visible photon that has a wavelength of 500 nm.
- Find the velocity of an electron having the same momentum.
- What is the energy of the electron, and how does it compare with the energy of the photon?
Strategy
Finding the photon momentum is a straightforward application of its definition: p=hλ.
If we find the photon momentum is small, then we can assume that an electron with the same momentum will be nonrelativistic, making it easy to find its velocity and kinetic energy from the classical formulas.
Solution for (a)
Photon momentum is given by the equation: p=hλ.
Entering the given photon wavelength yields
p=6.63×10−34J⋅s500×10−0m=1.33×10−27kg⋅m/s.
Solution for (b)
Since this momentum is indeed small, we will use the classical expression p=mv to find the velocity of an electron with this momentum. Solving for v and using the known value for the mass of an electron gives
v=pm=1.33×10−27kg⋅m/s9.11×10−31kg=1460m/s≈1460m/s.
Solution for (c)
The electron has kinetic energy, which is classically given by
KEe=12mv2.
Thus,
KEe=12(9.11×10−31kg)(1455m/s)2=9.64×10−25J.
Converting this to eV by multiplying by (1eV)/(1.602×10−19J) yields
KEe=6.02×10−6eV.
The photon energy E is
E=hcλ=1240eV⋅nm500nm=2.48eV,
which is about five orders of magnitude greater.
Discussion
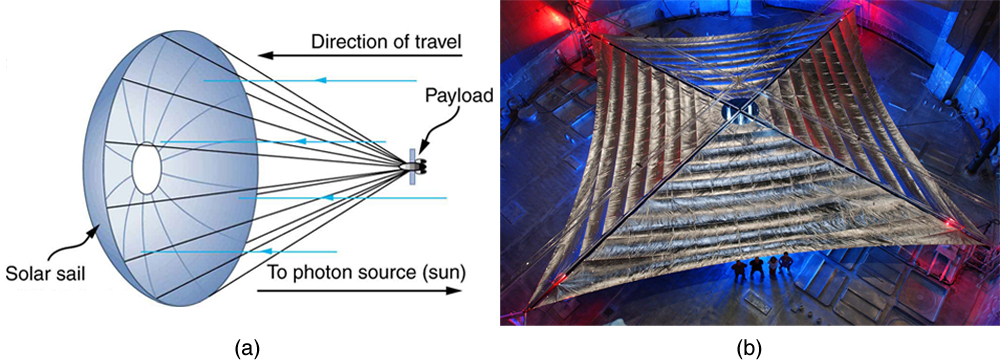
Photon momentum is indeed small. Even if we have huge numbers of them, the total momentum they carry is small. An electron with the same momentum has a 1460 m/s velocity, which is clearly nonrelativistic. A more massive particle with the same momentum would have an even smaller velocity. This is borne out by the fact that it takes far less energy to give an electron the same momentum as a photon. But on a quantum-mechanical scale, especially for high-energy photons interacting with small masses, photon momentum is significant. Even on a large scale, photon momentum can have an effect if there are enough of them and if there is nothing to prevent the slow recoil of matter. Comet tails are one example, but there are also proposals to build space sails that use huge low-mass mirrors (made of aluminized Mylar) to reflect sunlight. In the vacuum of space, the mirrors would gradually recoil and could actually take spacecraft from place to place in the solar system (Figure 29.4.3).
Relativistic Photon Momentum
There is a relationship between photon momentum p and photon energy E that is consistent with the relation given previously for the relativistic total energy of a particle as
E2=(pc)2+(mc2)2.
We know m is zero for a photon, but p is not, so that Equation ??? becomes
E=pc, or p=Ec(for photons).
To check the validity of this relation, note that E=hc/λ for a photon. Substituting this into p=E/c yields
p=(hc/λ)/c=hλ,
as determined experimentally and discussed above. Thus, p=E/c is equivalent to Compton’s result p=h/λ. For a further verification of the relationship between photon energy and momentum, see Example 29.4.3.
Photon Detectors
Almost all detection systems talked about thus far—eyes, photographic plates, photomultiplier tubes in microscopes, and CCD cameras—rely on particle-like properties of photons interacting with a sensitive area. A change is caused and either the change is cascaded or zillions of points are recorded to form an image we detect. These detectors are used in biomedical imaging systems, and there is ongoing research into improving the efficiency of receiving photons, particularly by cooling detection systems and reducing thermal effects.
Example 29.4.2: Photon Energy and Momentum
Show that p=E/c for the photon considered in the Example 29.4.2.
Strategy
We will take the energy E found in Example29.4.2, divide it by the speed of light, and see if the same momentum is obtained as before.
Solution
Given that the energy of the photon is 2.48 eV and converting this to joules, we get
p=Ec=(2.48eV)(1.60×10−19J/eV)3.00×108m/s=1.33×10−27kg.
Discussion
This value for momentum is the same as found before (note that unrounded values are used in all calculations to avoid even small rounding errors), an expected verification of the relationship p=E/c. This also means the relationship between energy, momentum, and mass given by E2=(pc)2+(mc)2 applies to both matter and photons. Once again, note that p is not zero, even when m is.
PROBLEM-SOLVING SUGGESTIONS
Note that the forms of the constants h=4.14×10−15eV⋅s and hc=1240eV⋅nm may be particularly useful for this section’s Problems and Exercises.
Summary
- Photons have momentum, given by p=hλ, where λ is the photon wavelength.
- Photon energy and momentum are related by p=Ec, where E=hf=hc/λ for a photon.
Glossary
- photon momentum
- the amount of momentum a photon has, calculated by p=hλ=Ec
- Compton effect
- the phenomenon whereby x rays scattered from materials have decreased energy


