1.2: Basic Trigonometry

Though trigonometry is mentioned as a prerequisite for this book, for the sake of completeness, this section will cover the trigonometry required for our purposes. This section will use degrees as its default unit. The next subsection shall introduce the concept of radians.

Our primary use for trigonometry will be for resolving vectors into their components and hence we will mostly deal with right-angled triangles.

Right-angled triangle

A right-angled triangle is one which has two mutually perpendicular sides. The side opposite to the right-angle is called the hypotenuse.

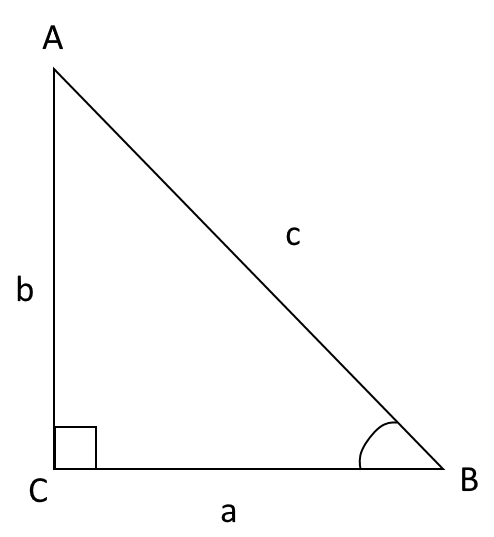
It is given that \(\angle C \) is 90^o. By the triangle angle sum rule, we know that the sum of internal angles must always be 180^o. Therefore, we can conclude that \(\angle A \) and \(\angle B \) are both acute, and that their sum is 90^o. Keep this point in mind. It will allow us to reduce the number of trigonometric functions to remember from three down to just one.

Trigonometric Functions

There are a total of six trigonometric functions, all representing distinct qualities of a triangle. For our purposes, the two most important functions are the sine \(\sin \theta \) and cosine \(\cos \theta \) functions. But, both of these functions can be represented by just the sine function. In fact, all trigonometric functions can be converted into their corresponding sine functions by using the appropriate angle.

All these functions represent the ratios of two sides from the triangle.

Sine:

The sine function is defined by the ratio of the side opposite to the angle to the hypotenuse. In our example, \(\sin \angle B \) is \(\dfrac{b}{c}).

If you recall the Pythagoras theorem, \(a^2 + b^2 = c^2 \), it is quite obvious that the value of the sine function lies between 0 and 1. If we choose to go beyond 90^o (discussed below), the values can be negative as well. However, the absolute value is still between 0 and 1.

This is the graph of the function \(\sin x \):

 

Below is a table of common values of sine:

Angle \(\theta \)	0^o	30^o	45^o	60^o	90^o
\(\sin \theta \)	0	\(\dfrac{1}{2} \)	\(\dfrac{1}{\sqrt{2}} \)	\(\dfrac{\sqrt{3}}{2} \)	1

You might notice that we have defined the values for angles that obviously cannot exist in a right-angled triangle, i.e. 0^o and 90^o. But let us think a bit about what they could mean. An angle of 0^o would imply that the "opposite" side is 0. An angle of 90^o would mean that the hypotenuse and "opposite" side coincide, and are equal. Of course, in these cases, we would effectively be dealing with lines, but imagining them as extreme cases of a triangle is useful for the sake of internalizing the concepts.

Cosine:

As the name implies, the cosine is the complementary ratio of sine. It is the ratio of the non-hypotenuse side adjacent to the angle to the hypotenuse. For the same reasons as the sine function, the function has a range of -1 to 1.

In the example of \(\angle B \), \(\cos \angle B = \dfrac{a}{c} \)

This is a graph of the function \(\cos x \):

 

Below is a table of common values of cosine:

Angle \(\theta \)	90^o	60^o	45^o	30^o	0^o
\(\cos \theta \)	0	\(\dfrac{1}{2} \)	\(\dfrac{1}{\sqrt{2}} \)	\(\dfrac{\sqrt{3}}{2} \)	1

Notice how the values of sine and cosine are related. As the value of sine increase, that of cosine decreases. Mathematically, we say these functions have a phase difference of 90^o. This is actually quite logical, as the "opposite" side of \(\angle B \) is the adjacent side of \(\angle A \). This is a very powerful insight. The sine of an angle is the cosine of its complementary angle. Mathematically,

\(\sin{\angle B} = \cos{\angle A} \)