2.3: Scientific Models
( \newcommand{\kernel}{\mathrm{null}\,}\)
Physical and Empirical Models
A model is a representation of something that is often too difficult (or impossible) to observe or display directly. Although a model is justified by experimental tests, it is only accurate in describing certain aspects of a physical system. For example, a model of color vision which accounts for the response of the eye to different colors, but not for the processing of that information by the brain[1]Such a model is not complete, but is still useful for some purposes, such as designing digital displays or represent a situation in the form of a computer simulation. Check out this interactive simulation of color vision.
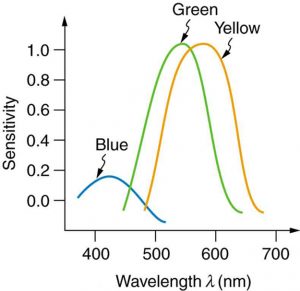
The graph shows the relative sensitivity of the three types of cones, which are named according to light wavelengths (colors) of greatest sensitivity. Evidence for the three types of cones comes from direct measurements in animal and human eyes and testing of color blind people. Image Credit: OpenStax College Physics
Physical models (mechanistic models) that explain how a system works, like the color vision model, can become theories after a preponderance of evidence has been built supporting their validity. Empirical models, which use mathematical trends in observed data, cannot become theories, but they are still useful for making decisions once they have sufficiently been validated.
Qualitative and Quantitative Models
Both physical and empirical models can be either qualitative or quantitative. Qualitative models predict what behavior you should observe, while quantitative models predict behaviors to observe and actual values to measure. The following table will help you understand the different types of models. The amount of information increases as you move from upper left to lower right of the table.
| Empirical | Physical | |
| Qualitative | When you drop something, it falls to the ground. | When you drop something it falls due to mutual gravitational attraction with the Earth |
| Quantitative | Without air resistance, everything falls with the same acceleration value of 9.8 m/s/s. | Combining Newton’s Law of Universal Gravitation and Newton’s 2nd Law of Motion the calculated free-fall acceleration for objects at the surface of the Earth is of 9.8 m/s/s. |
Stay tuned, the Unit 2 lab will produces a quantitative empirical model for the fall time of certain objects from a certain height when air resistance is present.
Computer Models
Computer modeling is a relatively new tool for science, but it still fits right into the overall process. Computer models are often used to assist in making predictions to be tested experimentally. Sometimes computer models are used as surrogates for expensive, time consuming, or complex, experiments to inform the experimental design process. However computer models are not permanent substitutes for experimentation and the results of computer models should be verified by experimentation or observational data. Computer models which have been verified against data are exceptionally helpful in making predictions for decision making. For example modeling high altitude winds to plan airliner flight paths and modeling storm paths to plan emergency procedures.
- [1] OpenStax University Physics, University Physics Volume 1. OpenStax CNX. Jun 5, 2018http://cnx.org/contents/d50f6e32-0fda-46ef-a362-9bd36ca7c97d@10.16.↵


