7.1: Strength of Human Bones
- Page ID
- 17758
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)The Femur
“In human anatomy, the femur (thigh bone) is the longest and largest bone. Along with the temporal bone of the skull, it is one of the two strongest bones in the body. The average adult male femur is 48 cm (18.9 in) in length and 2.34 cm (0.92 in) in diameter and can support up to 30 times the weight of an adult.”[1]
The Human Femur. Image Credit: Anatomography via Wikimedia Commons
Compression
When you place an object on top of a structure, the object’s weight tends to compress the structure. Any push that tends to compress a structure is called a compressive force. The average weight among adult males in the United States is 196 lbs (872 N)[3]. According to the statement that the femur can support 30x body weight, the adult male femur can support roughly 6,000 lbs of compressive force! Such high forces are rarely generated by the body under its own power, thus motor vehicle collisions are the number one cause of femur fractures[4].
Tension
When you hang an object from a structure the object’s weight will tend to stretch the structure. The structure responds by providing a tension force to hold up the object. Tension forces are restoring forces produced in response to materials being stretched. Non-rigid objects like ropes, cables, chains, muscles, tendons, can effectively provide tension forces only, while rigid object can supply compression and tension forces. For example, the biceps muscle is providing a tension (T) force on the thumb-side forearm bone (radius bone).
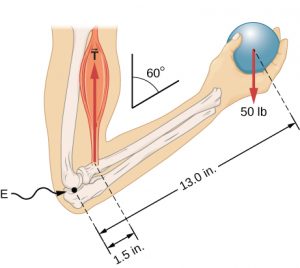
The elbow joint flexed to form a 60° angle between the upper arm and forearm while the hand holds a 50 lb ball . Image Credit: Openstax University Physics
Stress
The maximum compression or tension forces that a bone can support depends on the size of the bone. More specifically, the more area available for the force to be spread out over, the more force the bone can support. That means the maximum forces bones, (and other objects) can handle are proportional to the ccross-sectional area of the bone that is perpendicular (90°) to the direction of the force. For example, the force that the femur can support vertically along its length depends on the area of its horizontal cross-section which is roughly circular and somewhat hollow (bone marrow fills the center space).
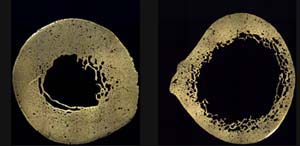
These cross sections show the midshaft of the femur of an 84-year-old female with advanced osteoporosis (right), compared to a healthy femur of a 17-year-old female (left). Image Credit: Smithsonian National Museum of Natural History
Larger bones can support more force, so in order to analyze the behavior of the bone material itself we need to divide the force applied to the bone by the minimum cross-sectional area (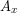 ). This quantity is known as the stress (σ) on the material. Stress has units of force per area so the SI units are (N/m2) which are also known as Pascals. Units of pounds per square inch (PSI, lbs/in2) are common in the U.S.
). This quantity is known as the stress (σ) on the material. Stress has units of force per area so the SI units are (N/m2) which are also known as Pascals. Units of pounds per square inch (PSI, lbs/in2) are common in the U.S.
(1)
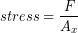
Reinforcement Exercises
Estimate the compressive stress within a 1.0 cm x 2.0 cm Lego block when you step on it with full body weight in units of pb_glossary id=”3977″]Pascals[/pb_glossary]. [Hint: We want the result in SI units, so convert the length and width to meters before calculating the cross-sectional area and use SI units for your weight.]
Ultimate Strength of the Femur
The maximum stress that bone, or any other material, can experience before the material begins fracture or rupture is called the ultimate strength. Notice that material strength is defined in terms of stress, not force, so that we are analyzing the material itself, without including the effect of how much material is present. For some materials the ultimate strength is different when the stress is acting to crush the material (compression) versus when the forces are acting to stretch the material under tension, so we often refer to ultimate tensile strength or ultimate compressive strength. For example, the ultimate compressive strength for human femur bone is measured to be 205 MPa (205 Million Pascals) under compression along its length. The ultimate tensile strength of femur bone under tension along its length is 135 MPa.[7] Along with bone, concrete and chalk are other examples of materials with different compressive and tensile ultimate strengths.
Reinforcement activity
Try to crush a piece of chalk by using your fingers to push on the ends and compress it along the long axis, no bending allowed. Any luck?
Now use your fingers to break the chalk by pulling it apart, straight along the long axis, again no bending allowed. Any luck?
Record your results and explain what they tell you about the compressive ultimate strength and tensile ultimate strength of chalk.
Compare and contrast the behavior you observed for chalk with the known behavior of bone and concrete. Cite your sources.
Everyday Example
Let’s check to see if the measured values for compressive ultimate strength agree with the claim that the human femur can support 30x the adult body weight, or roughly 6,000 lbs
First let’s to convert the claimed 6,000 lbs force to Newtons and work in SI units.
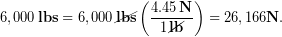
An approximate minimum cross-sectional area of the femur is 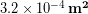 . (*See the bottom of this example if you are interested in learning how we approximated this value). We divide the compressive force by the cross-sectional area to find the compressive stress on the bone.
. (*See the bottom of this example if you are interested in learning how we approximated this value). We divide the compressive force by the cross-sectional area to find the compressive stress on the bone.
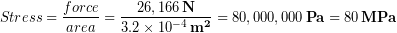
Our approximate value for the ultimate strength of bone that would be required to support 30x body weight was 80 MPa, which is actually less than the measured value of 205 MPa, so the claim that the femur can support 30x body weight seems reasonable.
*This is how we approximated the femur cross-sectional area, skip this if you aren’t interested:
First we divide the 2.34 cm femur diameter quoted earlier by two to find the femur radius, then we convert to standard units of meters.
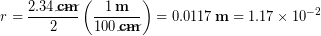
Using the equation for the area of a circle we calculate the total area of the femur to be:
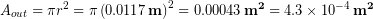
Finally we have to subtract off the area of the hollow middle part to get the net bone area. We used a ruler on the above picture of the femur cross-sections to see that the inner radius is roughly half of the outer radius, or 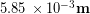 so we calculate the missing inner area:
so we calculate the missing inner area:
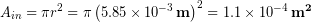
And subtract off the inner area from the total:
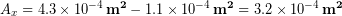
Transverse Ultimate Strength
So far we have discussed ultimate strengths along the long axis of the femur, known as the longitudinal direction. Some materials, such as bone and wood, have different ultimate strengths along different axes. The ultimate compressive strength for bone along the short axis (transverse direction) is 131 MPa, or about 36% less than the 205 MPa longitudinal value. Materials that have different properties along different axes are known as anisotropic. Materials that behave the same in all directions are called isotropic.
An interesting fact to finish up this chapter: when a person stands the femur actually experiences compressive and tensile stresses on different sides of the bone. This occurs because the structure of the hip socket applies the load of the body weight off to the side rather than directly along the long axis of the bone.
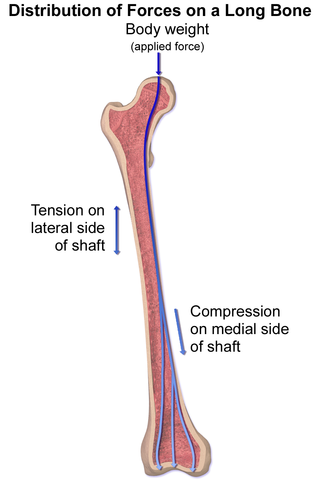
Both tension and compressive stresses are applied to the Femur while standing. Image Credit: Blausen Medical via Wikimedia Commons
- "Femur" by Orthapaedics One↵
- By Anatomography [CC BY-SA 2.1 jp (https://creativecommons.org/licenses/by-sa/2.1/jp/deed.en)], via Wikimedia Commons↵
- "Body Measurement" by FastStats, U.S. Centers for Disease Control is in the Public Domain↵
- "Femur Shaft Fractures" by OrthoInfo, American Academy of Orthopaedic Surgeons↵
- OpenStax University Physics, University Physics Volume 1. OpenStax CNX. Jul 11, 2018 [1]http://cnx.org/contents/d50f6e32-0fda-46ef-a362-9bd36ca7c97d@10.18. ↵
- "Effects of a Chronic Condition: Osteoporosis" by Written in Bone, Smithsonian National Museum of Natural History ↵
- "Elastic anisotropy of bone" by Rod Lakes , College of Engineering, University of Wisconson↵
- Blausen.com staff (2014). "Medical gallery of Blausen Medical 2014". WikiJournal of Medicine 1 (2). DOI:10.15347/wjm/2014.010. ISSN 2002-4436. [CC BY 3.0 (https://creativecommons.org/licenses/by/3.0)], from Wikimedia Commons ↵


