7.6: Modeling Body Tissues as Springs*
( \newcommand{\kernel}{\mathrm{null}\,}\)
Spring Constants of Body Parts
When tissues are put under stress within their elastic region they exert a restoring force that is proportional to the displacement. They also return back to their original size and shape when the force causing the deformation is removed. This exactly how springs behave, so we can model tissues, and any other material within its elastic region, as a collection of springs.
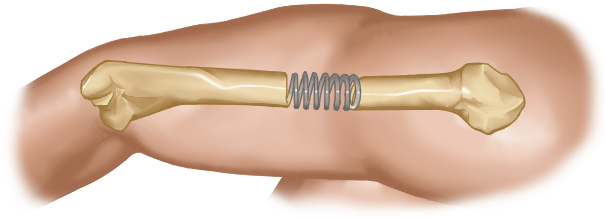
Artist’s conception of the elastic behavior body tissues. “Armcoil” by Sasha Lynch.
Consider modeling the humerus bone as a spring, as depicted in the image above. We can think of compressing a bone that has twice the cross-sectional area of the humerus as equivalent to compressing two of the original springs at the same time, which would require twice the applied force to create the compression distance (displacement). Therefore that bone would have twice the spring constant of the humerus. We can also think of a bone that is twice as long as the humerus as equivalent to compressing two of the original springs placed end-to-end. Each spring will only have to compress half of the total distance, so that would require only half the force to create the same total compression distance. Now we can see that the size of an object affects the spring constant. As a result, the force required to achieve a particular compression or stretch is different for different sized objects, even when they are made of the same material. In order to study the elastic properties of a material such as bone, independent of how big the bone is, then we need to remove the effect of size. That is why we have been working with stress, strain, and elastic modulus rather than force, displacement, and spring constant.
Relating Spring Constant and Elastic Modulus
We have learned that the spring constant tells us how much force is required to stretch a spring a certain distance. We have also learned that the elastic modulus tells us how much stress is required to cause a certain strain. It seems like these concepts are very similar, but not quite identical, which is true. The stress and strain relation within the linear region is really just Hooke's Law after accounting for the amount and shape of the material being deformed, which allows us to analyze the material itself independent of the size of the object. Let’s see how elastic modulus and spring constant are related.
If we start with the elastic stress-strain relation:
(1)
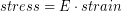
And then replace stress and strain with their definitions from previous chapters:
(2)
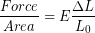
We can rearrange to get force and stretch distance on opposite sides
(3)
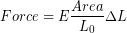
Which looks exactly like Hooke’s Law if the spring constant of an object is just all the stuff sitting in front of the stretch distance:
(4)
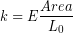
Now we can see that the elastic property of materials causes them to behave like springs. The human body has adapted to take advantage of the springy nature of tissues to walk more efficiently, jump higher, and generally improve performance in many activities. Upcoming units will help us to understand the physics behind these adaptations.
Everyday Example
Earlier we stated that a typical Achilles tendon would stretch by about the width of a human hair when an additional 480 lbs (2135 N) of tension was applied after un-crimping. How did we arrive at that surprising figure?
First we looked up the elastic modulus of the Achilles tendon and found the value to be 1.2 GPa.[1]
Then we looked up the typical length and diameter of the Achilles tendon and found 0.15 m for the length and 0.018 m for the minimum diameter. [2]
We approximated the cross-sectional area by assuming the tendon cylindrical with circular cross-section:
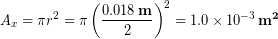
Then we inserted the elastic modulus, original length, and area into the equation for spring constant:
(5)
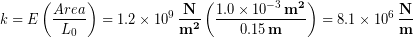
Now that we have the spring constant for a typical tendon, we used Hooke's Law to relate the tendon force and the stretch distance.
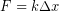
Dividing both sides by 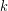 isolates the stretch distance, which is what we want. Then we insert the k and F values, remembering to use Newtons for our force unit to match the units on the spring constant we calculated.
isolates the stretch distance, which is what we want. Then we insert the k and F values, remembering to use Newtons for our force unit to match the units on the spring constant we calculated.
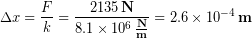
We can write our answer above in scientific notation as 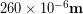 or using a metric prefix
or using a metric prefix 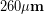 . Typical human hair is also a few hundred
. Typical human hair is also a few hundred 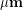 as you can see from this 2000x magnification image of a human hair produced by a scanning electron microscope (SEM).
as you can see from this 2000x magnification image of a human hair produced by a scanning electron microscope (SEM).

Human hair imaged with a scanning electron microscope at 2000x magnification. Notice the green scale bar on lower left showing 10 μm, indicating that the hair is roughly 100 μm in diamter. Image credit: “Human Hair 2000X” by MUSE via Wikimedia Commons
- "In vivo human tendon mechanical properties" by Constantinos N Maganaris and John P Paul, U.S. National Library of Medicine, National Institutes of Health↵
- "Achilles tendon: functional anatomy and novel emerging models of imaging classification" by Angelo Del Buono, Otto Chan, and Nicola Maffulli, U.S. National Library of Medicine, National Institutes of Health↵
- "Human Hair 2000X" by MUSE via Wikimedia Commons [CC BY-SA 3.0 (https://creativecommons.org/licenses/by-sa/3.0)] ↵


