7.4: Elasticity of Tendons and Bones
( \newcommand{\kernel}{\mathrm{null}\,}\)
Stress and Strain in Tendons
Tendons (attaching muscle to bone) and ligaments (attaching bone to bone) have somewhat unique behavior under stress. Functionally, tendons and ligaments must stretch easily at first to allow for flexibility, corresponding to the toe region of the stress-train curve shown below, but then resist significant stretching under large stress to prevent hyper-extension and dislocation injuries. A high resistance to large strain also helps to keep them in the elastic region and stay out of the plastic region, which corresponds to tissue damage.
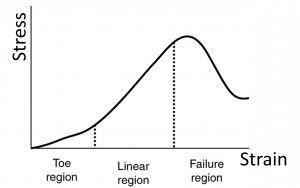
Typical stress-strain curve for mammalian tendon. Three regions are shown: (1) toe region (2) linear region, and (3) failure region. Image adapted from OpenStax College Physics.
The structure of the tendon creates this specialized behavior. To create the toe region, a small stress causes the fibers in the tendon begin to align in the direction of the stress, or uncrimp, and the re-alignment provides additional length. Then in the linear region, the fibrils themselves will be stretched.
Elastic Modulus
Within the linear region there is a constant relation between changes in stress and changes in strain, so the slope of the stress vs. strain curve is constant. That slope, known as the elastic modulus (E) or Young's modulus of the material, tells how resistant that material is to strain when put under stress within the elastic region. Higher elastic modulus means greater stress is required to get a certain amount of strain (e.g. stretch).
Reinforcement Activity
Hang a rubber band from a cabinet knob, doorknob or other feature. Use a paperclip or tape to hang a plastic cup or baggie or other container to the rubber band. Measure the length of the rubber band. Start adding pennies, five at a time, to the container. Measure the distance the rubber band stretches with each addition and calculate the strain for each case. Do this until you have added 25 pennies and record your results. Now look at the strain values you have and find how much the strain changed between each addition of pennies.
The change in stress is the same between each test because you add the same number of pennies each test, but is the change in strain you measured the same each time?
Are you in the linear region throughout this experiment? Explain.
Look up the weight of a penny, measure the cross-sectional area of your rubber band, and calculate the stress you applied with 10 pennies.
Use your stress and strain values for 10 pennies to calculate the elastic modulus of the rubber band.
Writing the linear relationship between changes in stress (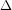 ) and changes in strain(
) and changes in strain(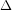 ) as an equation allows us to find stress or strain if we know the other one:
) as an equation allows us to find stress or strain if we know the other one:
(1)
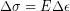
To find out how much strain will occur for a certain stress, we divide the stress by elastic modulus:
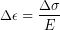
To find the elastic modulus we can to measure how much change in strain caused by a change in stress (or vice versa), which you may do in the lab for this unit:
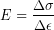
Just as for the ultimate strength, some materials have a different elastic modulus when the stress is applied along different axes, or even between tension and compression along the same axis. For example, the tensile elastic modulus of bone is 16 GPa (16 x 109 Pa) compared to 9 GPa under compression.[2] Check out the engineering toolbox for a massive tensile elastic modulus table. For more information on stress and strain in human tissues, including excellent diagrams, check out posted lecture notes from Professor Tony Leyland at Simon Fraser University.
- OpenStax, College Physics. OpenStax CNX. Aug 6, 2018 http://cnx.org/contents/031da8d3-b525-429c-80cf-6c8ed997733a@13.1. ↵
- OpenStax, College Physics. OpenStax CNX. Aug 6, 2018 [1]http://cnx.org/contents/031da8d3-b525-429c-80cf-6c8ed997733a@13.1. ↵