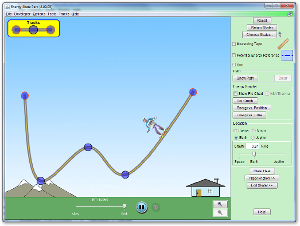
10.7: Surviving a Fall
( \newcommand{\kernel}{\mathrm{null}\,}\)
Mechanical Energy
When you do work to lift an object and then release it, the energy converts back to kinetic energy as the object falls. This process appears similar to the storage and release of elastic potential energy that we learned about in the previous chapter and suggests that we define a gravitational potential energy (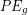 ). It’s not obvious where gravitational potential energy is stored, but for our purposes can treat it as being stored within the system comprised of the Earth and the objects we are moving around. The elastic potential energy, gravitational potential energy and kinetic energy are forms of mechanical energy. Forces and corresponding work that convert energy between forms of mechanical energy within a system are known as conservative forces and conservative work. We introduce these new terms because there are many cases when only conservative forces are acting and so energy just transfers between the forms of mechanical energy within the system. For such cases, any increase in potential energy is offset by a decease in kinetic energy and vice versa, so we know
). It’s not obvious where gravitational potential energy is stored, but for our purposes can treat it as being stored within the system comprised of the Earth and the objects we are moving around. The elastic potential energy, gravitational potential energy and kinetic energy are forms of mechanical energy. Forces and corresponding work that convert energy between forms of mechanical energy within a system are known as conservative forces and conservative work. We introduce these new terms because there are many cases when only conservative forces are acting and so energy just transfers between the forms of mechanical energy within the system. For such cases, any increase in potential energy is offset by a decease in kinetic energy and vice versa, so we know 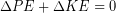 . Non-conservative forces do work that converts between mechanical energy, thermal energy, or chemical potential energy (we will learn more about chemical potential energy soon). Friction, drag force, air resistance, forces caused by muscular contractions, and forces resulting in permanent deformation are examples of non-conservative forces.
. Non-conservative forces do work that converts between mechanical energy, thermal energy, or chemical potential energy (we will learn more about chemical potential energy soon). Friction, drag force, air resistance, forces caused by muscular contractions, and forces resulting in permanent deformation are examples of non-conservative forces.
Reinforcement Exercises
Calculate the work you must do to raise 10 kg metal ball by a height of 10 m.
Work is a transfer of energy, in this case chemical potential energy in your body was transferred to what type of energy?
Was this a conservative work?
If you then dropped the ball, what kinetic energy would the object have just as it reached the ground (ignoring any work done by air resistance so that only gravity acts on the ball)? [Hint: Are there any non-conservative forces acting during the fall?]
What would be the speed of the ball immediately before impact with the ground?
Check out this simulation, which shows how energy is transferred among different types.
Conservation of Energy
Considering the Principle of Conservation of Energy we expect that any change to the total energy of a system must correspond to energy being transferred to the system from outside the system by an external net work on the system. Our observations have confirmed this expectation and are summarized by the Law of Conservation of Energy:
(1)
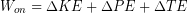
Gravitational Potential Energy
According to the Law of Conservation of Energy, if we do work to lift an object farther from the Earth without increasing its kinetic energy or thermal energy we must have increased the gravitational potential energy by the same amount as the work. The force we need to apply is the object’s weight, or (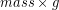 ) and the distance we over which we apply the force is the change in height
) and the distance we over which we apply the force is the change in height 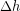 . Therefore the work we did was:
. Therefore the work we did was: 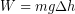 and this must be the same the amount that we have changed the gravitational potential energy.
and this must be the same the amount that we have changed the gravitational potential energy.
(2)
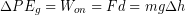
Note that the previous equation automatically gives a decrease in gravitational potential energy when an object gets lower because the change in height will be negative. The work done to lift an object is an example of useful work, or work done on the outside environment.[1]
Reinforcement Exercises
Calculate the change in gravitational potential energy when you climb 10 m high set of stairs.
How much useful work did you do while climbing the stairs?
Your body is not 100% efficient, so you actually did a bunch of additional work that didn’t increase your gravitational potential energy, but increased thermal energy instead. We will learn more about your body’s efficiency in the next unit.
Everyday Example: Rock Climbing Fall
A rock climber is 3.5 m above their last anchor point and fall. They will fall back 3.5 m back to the anchor point and then another 3.5 m below it before the rope comes tight for a total fall distance of 7.0 m (there was 3.5 m of rope out when they fell, so they will have to end up hanging by 3.5 m of rope). Neglecting air resistance, how fast will they be moving when the rope begins to come tight?
We will apply the Law of Conservation of Energy during the fall.
(3)
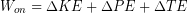
Neglecting air resistance there are no forces other than gravity on the person during the fall, so only conservative forces are acting and mechanical energy is conserved:
(4)
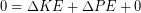
Next we write out the changes in each type of energy:
(5)
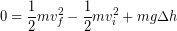
We recognize the initial speed was zero at the start of the fall and that we can divide every term in our equation by mass mass to cancel it out:
(6)
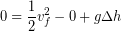
Then we isolate the speed:
(7)
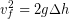
Finally we take the square root:
(8)
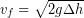
The climber fell 7.0 m, so the change in height was actually -7.0 m. We are ready to calculate the final speed:
(9)
![]()
Reinforcement Exercises
The climber in the example problem above will be caught by the rope. Do you think the rope should be designed to stretch so the catch occurs over a long distance or a short one? Explain.
What is the kinetic energy of the climber just as the rope begins to come tight?
How much work must be done by the rope in order to bring the climber to a stop?
If the rope stretches by 0.50 m while catching the climber, what is the average force applied to the climber? This type of stretchy dynamic rope is used in rock climbing. The rope only slightly elastic, (the climber doesn’t bounce back up to nearly their original height). The rope is designed so that system has a small coefficient of restitution and most of the energy in the fall is transferred into thermal energy during the process of stretching the rope.
If a static rope was used, so the stretch was only 0.05 m while catching the climber, what is the average force applied to the climber? This type of non-stretchy static rope should not be used for rock climbing.
- OpenStax, College Physics. OpenStax CNX. May 13, 2019 http://cnx.org/contents/031da8d3-b525-429c-80cf-6c8ed997733a@16.4↵