11.5: Measuring Body Temperature
- Page ID
- 17806
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Liquid Thermometers
We now know that an increase in temperature corresponds to an increase in the average kinetic energy of atoms and molecules. A result of that increased motion is that the average distance between atoms and molecules increases as the temperature increases. This phenomenon, known as thermal expansion is the basis for temperature measurement by liquid thermometer.
A clinical thermometer based on the thermal expansion of a confined liquid. Image Credit: Clinical Thermometer by Menchi via Wikimedia Commons
Common liquid thermometers use the thermal expansion of alcohol confined within a glass or plastic tube to measure temperature. Due to thermal expansion, the alcohol volume changes with temperature. The thermometer must be calibrated by marking the various fluid levels when the thermometer is placed in an environment with a known temperature, such as water boiling at sea level.
Reinforcement Exercise
You may have noticed that when you place a liquid thermometer into hot water, the liquid level actually drops momentarily, before beginning to climb as expected. Knowing what you do about thermal expansion, can you explain why this occurs?
Bimetallic Strips
Different materials will thermally expand (or contract) by different amounts when heated (or cooled). Bimetallic strips rely on this phenomenon to measure temperature. When two different materials are stuck together, the resulting structure will bend as the temperature changes due to the different thermal expansion experienced by each material.
The curvature of a bimetallic strip depends on temperature. (a) The strip is straight at the starting temperature, where its two components have the same length. (b) At a higher temperature, this strip bends to the right, because the metal on the left has expanded more than the metal on the right. At a lower temperature, the strip would bend to the left. Image Credit: Openstax University Physics
Linear Thermal Expansion
For most common materials the change in length (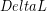
) caused by a change in temperature (
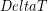) is proportional to the original length (
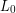) and can be modeled using the linear thermal expansion coefficient (
) and the following equation:
\[\Delta L=\alpha L_{0} \Delta T \label{1}\]
The following table provides the linear thermal expansion coefficients for different solid materials. More expansive (ha!) tables can be found online.
| Material | Coefficient of Linear Expansion (1/°C) |
|---|---|
| Solids | |
| Aluminum | 25 × 10−6 |
| Brass | 19 × 10−6 |
| Copper | 17 × 10−6 |
| Gold | 14 × 10−6 |
| Iron or steel | 12 × 10−6 |
| Invar (nickel-iron alloy) | 0.9 × 10−6 |
| Lead | 29 × 10−6 |
| Silver | 18 × 10−6 |
| Glass (ordinary) | 9 × 10−6 |
| Glass (Pyrex®) | 3 × 10−6 |
| Quartz | 0.4 × 10−6 |
| Concrete, brick | ~12 × 10−6 |
| Marble (average) | 2.5 × 10−6 |
Everyday Example
The main span of San Francisco’s Golden Gate Bridge is 1275 m long at its coldest. The bridge is exposed to temperatures ranging from –15 °C to 40 °C. What is its change in length between these temperatures? Assume that the bridge is made entirely of steel.
We can use the equation for linear thermal expansion:
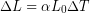
Substitute all of the known values into the equation, including the linear thermal expansion coefficient for steel and the initial and final temperatures:
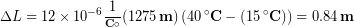
Although not large compared to the length of the bridge, the change in length of nearly one meter is observable and important. Thermal expansion could causes bridges to buckle if not for the incorporation of gaps, known as expansion joints, into the design.
Expansion joint on the Golden Gate Bridge. Image Credit: Expansion Joint Golden Gate Bridge by Michiel1972 via Wikimedia Commons
Reinforcement Exercises
A deep-space satellite made primarily of aluminum is 12 m long when launched at 22 °C (72 °F).
If the satellite comes eventually come to thermal equilibrium with the cosmic microwave background temperature at -270.45 °C (-455 °F).[4]
How much will the satellite change length?
What will the new length be?
Temperature Units
Thermometers measure temperature according to well-defined scales of measurement. The three most common temperature scales are Fahrenheit, Celsius, and Kelvin. On the Celsius scale, the freezing point of water is 0 °C and the boiling point is 100 °C. The unit of temperature on this scale is the degree Celsius (°C). The Fahrenheit scale (°F) has the freezing point of water at 32 °F and the boiling point 212 °F. You can see that 100 Celsius degrees span the same range as 180 Fahrenheit degrees. Thus, a temperature difference of one degree on the Celsius scale is 1.8 times as large as a difference of one degree on the Fahrenheit scale, as illustrated by the top two scales in the following diagram.
Relationships between the Fahrenheit, Celsius, and Kelvin temperature scales are shown. The relative sizes of the scales are also shown. Image Credit: Temperature Scales diagram from OpenStax University Physics[/footnote]
The Kelvin Scale
The definition of temperature in terms of molecular motion suggests that there should be a lowest possible temperature, where the average microscopic kinetic energy of molecules is zero (or the minimum allowed by the quantum nature of the particles). Experiments confirm the existence of such a temperature, called absolute zero. An absolute temperature scale is one whose zero point corresponds to absolute zero. Such scales are convenient in science because several physical quantities, such as the pressure in a gas, are directly related to absolute temperature. Additionally, absolute scales allow us to use ratios of temperature, which relative scales do not. For example, 200 K is twice the temperature of 100 K, but 200 °C is not twice the temperature of 100 °C.
) have the same value in both Kelvins and degrees Celsius. As a result, the freezing and boiling points of water in the Kelvin scale are 273.15 K and 373.15 K, respectively, as illustrated in the previous diagram.
Reinforcement Exercise
Convert 50 °F to °C and then to K.
Temperature Measurement
In addition to thermal expansion, other temperature dependent physical properties can be used to measure temperature. Such properties include electrical resistance and optical properties such as reflection, emission and absorption of various colors. Light-based temperature measurement will come up again in the next chapter.
- Clinical Thermometer by Menchi [GFDL (http://www.gnu.org/copyleft/fdl.html) or CC-BY-SA-3.0 (http://creativecommons.org/licenses/by-sa/3.0/)] via Wikimedia Commons↵
- OpenStax University Physics, University Physics. OpenStax CNX. May 10, 2018 http://cnx.org/contents/74fd2873-157d-4392-bf01-2fccab830f2c@5.301.↵
- Michiel1972 [CC BY-SA 3.0 (https://creativecommons.org/licenses/by-sa/3.0)], via Wikimedia Commons↵
- "Web-based hypothermia information: a critical assessment of Internet resources and a comparison to peer-reviewed literature" by Dr. Eric Christian, Cosmicopia, NASA is in the Public Domain↵
- Significant content in this chapter was adapted from OpenStax University Phyiscs which you can download for free at http://cnx.org/contents/a591fa18-c3f4-4b3c-ad3e-840c0a6e95f4@1.322.↵