11.12: Preventing Hyperthermia

Whole body hyperthermia is a method to raise a patient’s body temperature for the treatment of advanced cancer. This technique is based on laboratory studies that show cancer cells are more sensitive to heat injury than normal cells. Physicians induce hyperthermia using a high-flow water suit controlled by a microprocessor, a machine which closely monitors body temperature. The patient’s body temperature is raised by the insulated build-up of metabolic (body) heat, plus by the heat delivered by the warm-water suit. Image Credit: Hyperthermia Patient by Mike Mitchell (photographer) [Public domain], via Wikimedia Commons

^[1]

Hyperthermia, as opposed to hypothermia, occurs when body temperature increases as thermal energy builds up the body because heat is not transferred out of the body fast enough to keep up with the body’s thermal power. We can try to avoid such a situation by minimizing our work output to reduce overall thermal power (remember, the body has low efficiency so doing work means generating thermal energy). We can also use our understanding of the conduction, convection, and thermal radiation to ensure maximum heat transfer away from the body. For example, we can minimize the thickness of clothing to increase conduction, wear light colored clothing to reduce radiation absorbed from the sun, and encourage air circulation (convection).

The clothing warn by the people in this image was designed to minimize energy absorbed from the sun (light colors), not hinder conduction (thin), and allow convection (open, breathable). Image credit: OpenStax University Physics.

^[2]

Sweating

In some cases our thermal power outpaces the rate at which we exhaust heat by conduction, convection and radiation. Our strategy to deal with this situation is sweating. When we sweat some of the water on our skin evaporates into a water vapor. Only the molecules with the most kinetic energy are able to escape the attraction of their fellow water molecules and enter the air. Therefore the evaporating molecules remove more than a fair share of the thermal energy (thermal energy is just molecular kinetic energy remember). The remaining liquid water molecules then have less thermal energy on average, so they are at a lower temperature and must absorb more energy from your body as they come to thermal equilibrium with your body again. This evaporation process allows the body to dump thermal energy even when the environment is too warm for significant heat loss by conduction, convection, and radiation. The amount of energy removed by evaporation is quantified by the latent heat of vaporization (L_v). For water L_v = 2,260 kJ/kg, which means that for every kilogram of sweat evaporated, 2260 kiloJoules of energy is transferred away from the skin.

The liquid temperature is determined by the average of the kinetic energy of atoms and molecules. At any moment the molecules will have a range of individual kinetic energies, some will have greater energy than the average and some less. (a) Those molecules with sufficiently large kinetic energy can break away to the vapor phase even at temperatures below the ordinary boiling point. (b) If the container is sealed, evaporation will continue until the space above the water reaches 100% Relative Humidity, meaning there is so many water molecules in the vapor phase that they re-enter the liquid phase just as often as they evaporate. At 100% humidity evaporation will no longer provide a net cooling effect. Image Credit: OpenStax, Humidity, Evaporation, and Boiling

^[3]

Everyday Example

A person working in an environment that happens to be very close to body temperature (about 100 °F) would not be able to get rid of thermal energy by conduction, convection, or radiation. If the person was working hard and generating about 250 W of thermal power (similar to the thermal power while shivering) then how much sweat would need to be evaporated each hour to keep their body temperature from rising?

In order to keep the body temperature from rising the person needs to get rid of 250 W of thermal energy, that’s 250 J/s. Let’s convert that to Joules per hour:

(1)

Each kilogram of water that evaporates removes 2,260,000 J of energy, so only a fraction of a kilogram will need to be evaporated every hour:

(2)

The body would need to evaporate 0.4 kg per hour. Water has a density of about 1 kg/L, so that would be a volume of 0.4 L/hr, or roughly 1.7 cups/hr, or 13.5 fluid oz/hr.

Exercises

The visitor center at Zion National Park uses evaporative cooling towers to condition the inside air^[4]. During the day, the center receives heat from the environment through conduction, convection, and radiation. In order to maintain a constant temperature that heat must be removed, typically by an air conditioning system. At the visitor center, evaporation of water in the cooling towers removes heat so the air conditioning system doesn’t have to.

If the visitor center receives average of 45 MJ/hr of heat from the environment, what mass of water would need to be evaporated each hour (kg/hr) in order to counter-balance all 45 MJ/hr of incoming heat?

How many liters per hour of water would that be?

Heat Index

The Heat Index is a measure of how hot it really feels when relative humidity is factored in with the actual air temperature. To find the Heat Index temperature, look at the Heat Index Chart above or check our Heat Index Calculator. As an example, if the air temperature is 96°F and the relative humidity is 65%, the heat index–how hot it feels–is 121°F. The red area without numbers indicates extreme danger. Image Credit: “Heat Index” by National Weather Service, NOAA is in the Public Domain

^[5]

The rate at which water will evaporate depends on the liquid temperature and the relative humidity of the surrounding air. The relative humidity is a measure of how many water molecules are in the vapor phase relative to the maximum number that could possibly be in the vapor phase at at a given temperature. A relative humidity of 100% means that no more water molecules can be added to the vapor phase. If the humidity is high, then evaporation will be slow and may not provide sufficient cooling. The heat index takes into account both air temperature and the relative humidity to determine how difficult it will be for your body to exhaust heat. Specifically, the heat index provides the theoretical air temperature that would be required at 20% humidity to create the same difficulty in exhausting heat as the actual temperature and humidity. Heat index values were devised for shady conditions with a light wind. Exposure to full sun or stagnant air can increase values by up to 15 degrees!

Exercises

Which of the following situations has a greater heat index temperature, or “feels-like” temperature:

• 90 % Relative Humidity and 85 °F
• 40 % Relative Humidity and 96 °F

Boiling and The Bends

We have learned that evaporation takes place even when a liquid isn’t boiling, so we may be wondering what causes boiling and how is it different from normal evaporation? Water ordinarily contains significant amounts of dissolved air and other impurities, which are observed as small bubbles of air in a glass of water. The bubbles formed within the water so the relative humidity inside the bubbles is 100%, meaning the maximum possible number of water molecules are inside the bubble as vapor. Those molecules collide with the walls of the bubble causing an outward pressure. The speed of the water molecules increases with temperature, so the pressure they exert does as well. At 100 °C the internal pressure exerted by the water vapor is equal to the atmospheric pressure trying to collapse the bubbles, so rather than collapse they will expand and rise, causing boiling. Once water is boiling, any additional thermal energy input goes into changing liquid water to water vapor, so the water will not increase temperature. Turning up the burner on the stove will not cook the food faster, it will just more quickly boil away (evaporate) the water.

Everyday Examples: The Bends

At high altitude the atmospheric pressure is lower, so molecules of water vapor don’t need to create as much pressure within bubbles to maintain boiling. Therefore, boiling will occur at a lower temperature and cooking foods by boiling will take longer. (Food packaging often gives alternative cook times for high altitude).

The same process is responsible for the bends, which refers to the formation of nitrogen bubbles within the blood upon rapid ascent while SCUBA diving. You might imaging that you could hang out underwater by breathing through a hose, and that would work in very shallow water. However, the high pressure exerted by water at depths below roughly 2 m (6 ft) would prevent the diaphragm and rib cage from expanding to pull air into the lungs. At greater depths you need to breath from a pressurized container which helps to force air into your lungs against the additional hydrostatic pressure. Of course if you breathed from the container at shallow depth then the pressure would be too high and would cause damage to your lungs. A pressure regulator that outputs the appropriate pressure according to the water depth is the core of the SCUBA system.

There is always some gas dissolved in your blood, including carbon dioxide, oxygen, and nitrogen. The amount of dissolved gas is determined by the temperature and the pressure. If temperature is high enough, and pressure is low enough, then boiling will occur. Breathing high pressure air from a SCUBA system while at depth forces these gases to dissolve into your blood in the amounts determined by your body temperature and the high pressure.

When ascending, the pressure drops quickly, but the body temperature stays constant, so the blood gases can begin to boil, starting with Nitrogen. There is not issue with blood temperature here, blood is still at body temperature, but the bubbles are a problem for the cardiovascular system. To prevent the bends, you must ascend slowly, allowing the gasses to slowly escape from the blood and be expelled in the breath, without forming large bubbles in the blood.

To treat the bends a patient is placed in a hyperbaric (high pressure) chamber. The high pressure collapses the bubbles and prevents new ones from forming. The pressure is then slowly decreases to allow the blood gasses to escape slowly, simulating a gradual ascent.

Students at the Naval Diving and Salvage Training Center undergo various training scenarios to prepare them for duties involving underwater emergencies and procedures. Image Credit: “Decompression Chamber” by U.S. Navy Mass Communication Specialist 2nd Class Jayme Pastoric, via Wikimedia Commons.

^[6]

Latent Heats

We have learned that evaporation of liquid molecules removes thermal energy from the liquid. An exchange of thermal energy will accompany any such change of phase. The reverse process of condensation, in which vapor molecules stick together to form a liquid, will bring thermal energy into the liquid. The latent heat of vaporization also quantifies the energy exchanged during condensation.

Energy is required to partially overcome the attractive forces between molecules in a solid to form a liquid. That same energy must be removed for freezing to take place. (b) Molecules are separated by large distances when going from liquid to vapor, requiring significant energy to overcome molecular attraction. The same energy must be removed for condensation to take place. When causing a phase change by adding or removing thermal energy, there is no temperature change until the phase change is complete. Image Credit: OpenStax CNX

Changing from solid to liquid, known as melting, requires energy just as evaporation does. The thermal energy required to melt a solid will be pulled from the surrounding environment, thus lowering the environment temperature. In similar fashion to vaporization, the amount of energy removed by melting is quantified by a latent heat, in this case the latent heat of fusion (L_f). For water, L_f = 334 kJ/kg, which means that for every kilogram of ice melted, 334 kiloJoules of energy input is needed. Freezing releases the same amount of energy into the environment that melting requires as input. The temperature at which melting occurs (within a given pressure) is known as the melting point. The melting and boiling points and latent heats of various substances at standard atmospheric pressure are shown in the following chart:

Melting and Boiling points, and Latent Heats at Standard Atmospheric Pressure^[7][/footnote]

	Lf			Lv
Substance	Melting point (ºC)	kJ/kg	kcal/kg	Boiling point (°C)	kJ/kg	kcal/kg
Helium	−269.7	5.23	1.25	−268.9	20.9	4.99
Hydrogen	−259.3	58.6	14.0	−252.9	452	108
Nitrogen	−210.0	25.5	6.09	−195.8	201	48.0
Oxygen	−218.8	13.8	3.30	−183.0	213	50.9
Ethanol	−114	104	24.9	78.3	854	204
Ammonia	−75		108	−33.4	1370	327
Mercury	−38.9	11.8	2.82	357	272	65.0
Water	0.00	334	79.8	100.0	2256^5	539^6
Sulfur	119	38.1	9.10	444.6	326	77.9
Lead	327	24.5	5.85	1750	871	208
Antimony	631	165	39.4	1440	561	134
Aluminum	660	380	90	2450	11400	2720
Silver	961	88.3	21.1	2193	2336	558
Gold	1063	64.5	15.4	2660	1578	377
Copper	1083	134	32.0	2595	5069	1211
Uranium	1133	84	20	3900	1900	454
Tungsten	3410	184	44	5900	4810	1150

Reinforcement Exercises

Does it take more energy to melt 1 kg of ice or evaporate 1 kg of water? Explain how you know.

Everyday Examples: Melting Ice for Drinking Water

Spending more than a day in frozen landscapes (high altitude, high latitude, or both), will require melting ice/snow to make drinking water. Let’s determine the thermal energy required to melt 10 kg of ice that started at 0 °C.

First we look up the latent heat of fusion for water in the previous chart and find L_f = 334 kJ/kg, or 334,000 J/kg. Using this value in the latent heat formula:

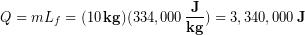
Now that we are familiar with the idea of latent heat, let’s combine that with our understanding of the energy required to change temperature, to get a full approximation of the minimum amount of stove fuel required for a three-person, round-trip expedition to the summit of Denali, North America’s highest mountain, at 20,380 ft (6495 m). Allowing for gradual acclimatization to altitude will reduce the likelihood of acquiring high altitude pulmonary edema and/or high altitude cerebral edema, so we will plan 21 days on the mountain.

First, let’s figure out how much water we need. The combination of acclimatization and climbing effort will require at least 4 liters of water per person per day. The total volume we need is then:

The density of water is 1 kg/L so we will also need 252 kg of water. To get that mass of water we will need to warm and melt that mass of snow each day. The average temperature on the mountain will be -20 °C and we will assume the snow to be melted starts off at this temperature. Let’s find the energy required to warm that mass of -20 °C snow up to 0 °C. We use a chart of specific heats to find c_ice = 2 kJ/kg = 2,000 J/kg. Using that value in our equation relating heat and temperature change:

Next we need the energy to melt the snow:

So far we need 10,080,000 J + 8,4168,000 J = 94,248,000 J to get ourselves enough water at 0 °C.

Typically the snow is brought to a boil to prevent sickness due to contamination by previous expeditions, and because a hot drink is great for mind and body after hauling a heavy pack and sled through deep snow for 12 hours in sub-zero temperatures at high altitude.

At altitude, the water will boil before reaching 100 °C. According to boiling point vs. altitude graph the boiling point of water at a mountain height of 13,000 ft will be about 190 °F (88 °C) rather than 212 °F (100°C). We will only need to raise the water temperature from 0 °C to 88 °C to achieve boiling. Water has a specific heat of 4186 J/(kg C°), so we have:

All told, we need that 92,828,736 J plus our previous 94,248,000 J for a total of 187,076,736 J.

According to data on energy densities in fuel, typical liquid fuels (white gas, gasoline, etc.) will provide roughly 40 MJ (40,000,000 J) of net heating energy per kg of fuel burned. To make our rough estimate the minimum fuel requirement we will assume all of the thermal energy released by burning the fuel is transferred to the water:

The density of liquid fuels is less than water at roughly 0.75 kg/L, so this minimum 4.7 kg of fuel comes out to about 6 liters, or 1.5 gallons. Accounting for heat loss from stove and pot to the environment (especially in windy conditions) the actual requirement could end up substantially greater, depending on conditions. On an actual 3-person, 21-day expedition to the summit of Denali in May of 2012 we used just under 2 gallons of fuel, so our estimate was pretty reasonable.

Reinforcement Exercises

A person having a heat stroke is placed in an ice bath with 3.0 kg of ice at 0.0 °C.

How much thermal energy would be removed from the body in order to melt all the ice?

How much would body temperature decrease do to the heat loss you calculated? (Assume an 80 kg body and ignore the fact that the body will be producing about 100 W of thermal power because that rate is very small compared to the overall rate of heat loss to the ice).

Check out the following simulations allows you to play with phase changes.

---

1. Hyperthermia Patient by Mike Mitchell (photographer) [Public domain], via Wikimedia Commons↵
   
2. OpenStax University Physics, University Physics Volume 2. OpenStax CNX. Feb 6, 2019 http://cnx.org/contents/7a0f9770-1c44-4acd-9920-1cd9a99f2a1e@15.2↵
   
3. OpenStax, Humidity, Evaporation, and Boiling. OpenStax CNX. Sep 9, 2013 http://cnx.org/contents/030347e9-f128-486f-a779-019ac474ff90@5↵
   
4. "Zion National Park Visitor Center" by National Renewable Energy Laboratory, U.S. Department of Energy is in the Public Domain↵
   
5. "Heat Index" by National Weather Service, NOAA is in the Public Domain↵
   
6. "Decompression Chamber" by U.S. Navy Mass Communication Specialist 2nd Class Jayme Pastoric, is in the Public Domain. ↵
   
7. [footnote]OpenStax CNX. Feb 27, 2019 http://cnx.org/contents/031da8d3-b525-429c-80cf-6c8ed997733a@14.44. ↵