7.2: Deforming Bones and Tendons
( \newcommand{\kernel}{\mathrm{null}\,}\)
Strain on the Achilles Tendon
When a person stands on one foot and raises their heel off the ground the Achilles’ tendon exerts about three times their body weight in tension. For a person weighing 160 lb (712 N) the Achilles’ tendon will experience 480 lbs (2135 N) of tension just to raise the heel and much more when jumping, landing, or pushing off the ground to change direction suddenly.
Even if the tension were doubled to 960 lbs, a healthy adult Achilles’ tendon should not rupture, but it will certainly stretch. However, the additional stretch due to the additional 480 lbs of tension will be about the width of a human hair! Specifically, it will stretch by roughly an additional 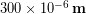 or 300 micrometers (μm). The Achilles Tendon is about 0.15 m long [1]so the percent stretch is only 0.2% . The amount a material stretches as a fraction of its original length is known as the strain(ε). (Sometimes strain is expressed as a percentage by taking the fractional strain and multiplying by 100).
or 300 micrometers (μm). The Achilles Tendon is about 0.15 m long [1]so the percent stretch is only 0.2% . The amount a material stretches as a fraction of its original length is known as the strain(ε). (Sometimes strain is expressed as a percentage by taking the fractional strain and multiplying by 100).
(1)
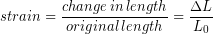
We need to be careful with the term strain because it has a different meaning in medical terminology where a strain is an over-stretching or tearing of muscle or tendon, which connect muscle to bones. A sprain is an over-stretching or tearing of ligaments, which connect bones together in joints.[2] The next sections will help you understand how materials, including ligaments and tendons, behave when they are over-stretched or torn in the context of physics.
Material Deformation
Before a material is stressed enough to fracture or rupture (while the stress is still less than the ultimate strength) the material will deform under the applied stress. The resistance of materials to being deformed is what causes the normal force (support force) we introduced in the unit on balance and stability. Materials will lengthen under tensile stress and shorten under compressive stress, causing strain. When the stress and strain are relatively small the material will behave like a spring or an elastic material and return to its original length when the stress is removed. The material is said to be operating in the elastic region. When the stress goes beyond the yield point the material will become permanently deformed and will not return to its original length when the stress is removed. The material has been pushed into the plastic region.
Stress vs. Strain Curves
If you apply stress to a material and measure the strain, or vice versa, you can create a stress vs. strain curve like the one shown below for a typical metal. Let’s discuss the important parts of the graph:
- The absolute highest point on the graph is the ultimate strength, indicating the onset of failure toward fracture or rupture.
- Notice that after reaching the ultimate strength, but before full failure, the stress can actually decrease as strain increases, this is because the material is changing shape by breaking rather than stretching or compressing the distance between molecules in the material.
- In the first part of the elastic region, the strain is proportional to the stress, this is known as the linear region.
- After the stress reaches the linearity limit (H) the slope is no longer constant, but the material still behaves elastically.
- The elastic region ends and the plastic region begins at the yield point (E). In the plastic region, a little more stress causes a lot more strain because the material is changing shape at the molecular level. In some cases the stress can actually decrease as strain increases, because the material is changing shape by re-configuring molecules rather than just stretching or compressing the distance between molecules.
- The green line originating at P illustrates the metal’s return to non-zero strain value when the stress is removed after being stressed into the plastic region (permanent deformation).
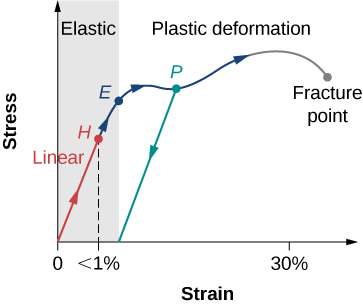
Typical stress-strain plot for a metal: The graph ends at the fracture point. The arrows show the direction of changes under an ever-increasing stress. Points H and E are the linearity and elasticity limits, respectively. The green line originating at P illustrates the metal’s return to a greater than original length when the stress is removed after entering the plastic region. Image Credit: OpenStax University Physics
- "Achilles tendon: functional anatomy and novel emerging models of imaging classification" by Angelo Del Buono, Otto Chan, and Nicola Maffulli, U.S. National Library of Medicine, National Institutes of Health↵
- "Sprains and Strains" by Patient care and health information, Mayo Clinic↵
- OpenStax University Physics, University Physics Volume 1. OpenStax CNX. Aug 2, 2018 http://cnx.org/contents/d50f6e32-0fda-46ef-a362-9bd36ca7c97d@11.1. ↵


