7.5: Measuring Weight
( \newcommand{\kernel}{\mathrm{null}\,}\)
Springs
We have learned that materials stretched within their linear region exhibit linear stress–strain behavior. Springs allow us to adjust the amount of strain that occurs for a given stress and increase the size of the linear region. For example, take a steel rod one foot in length and the diameter of a clothing thread and you would not be able to noticeably stretch that rod with your bare hands. However, if that rod were formed into a spring, then you could stretch the spring with your bare hands.
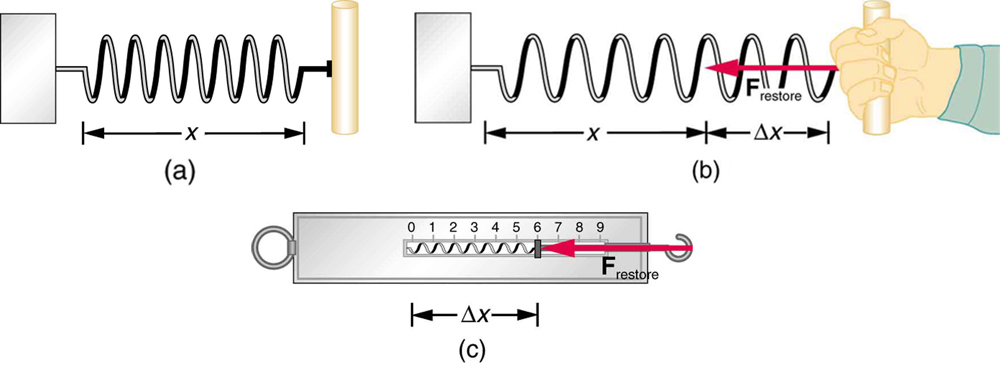
The force exerted on a stretched spring determines how far it stretches. (a) This spring has a length x when not stretched. (b) The resistance of the spring to deformation causes a force, Frestore to be exerted back on whatever is pulling on the hook. (c) A spring scale is one device that uses a spring to measure force. Image Credit: OpenStax University Physics
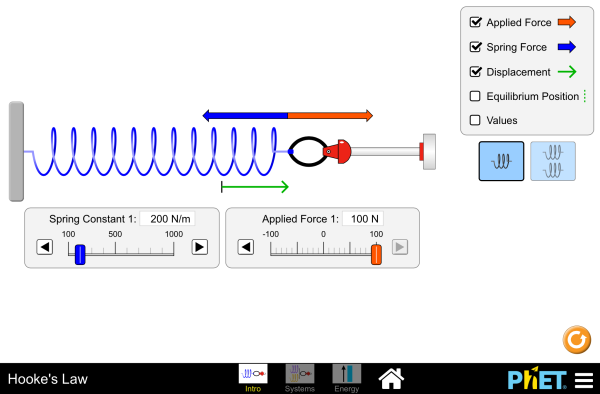
Springs follow Hooke's Law which states that the restoring force, FR exerted by the spring is equal to the stretch or compression distance, known as the displacement (Δx), multiplied by spring stiffness (k) and the direction of the force is opposite to the direction of the displacement.
(1)
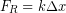
A higher spring stiffness means the spring shows a greater resistance to stretching or compressing. Spring stiffness is often called the spring constant.
Check out this simulation of Hooke's Law:
Reinforcement Activity
 is 3 cm, what is the spring constant (stiffness) in units of N/cm?
is 3 cm, what is the spring constant (stiffness) in units of N/cm?Weight with a Spring Scale
Spring scales are designed to take advantage of Hooke's law to determine the size of the force stretching the spring by measuring the displacement. In order to use a spring scale to measure weight we can multiply the measured stretch distance by the known spring constant to find the restoring force applied by the spring. Typically spring scales will have markings on them which indicate the restoring force for each stretch distance, so we don’t have to actually calculate the restoring force every time we use the scale. If the object being weighed is in equilibrium then the restoring force and the weight of the object are the same, and so by measuring the restoring force with the scale we then know the weight. For example when hanging the object from the spring scale the force of gravity will pull it down and the restoring force in the spring pulls it up, as in the image below. If instead the scale is tilted so gravity and restoring force don’t have opposite directions, the reading may be inaccurate. If the object and/or scale are not in equilibrium while holding it, then the reading may be inaccurate, and we will learn more about how and why in later units. Either way, the scale is only accurate if the object being weighed remains in equilibrium during the measurement.

Biologist Dr. Paula Khan holds still and keeps the scale vertical while she weighs a desert tortoise before release as part of the Fort Irwin, Calif., tortoise translocation. Photo Credit: “Paula Khan” by Neal Snyder via Wikimedia Commons
Many analog scales are based on multiple springs or the resistance to deformation by objects other than springs, but they still determine weight using measurement of a deformation combined with a known relation between deformation and force.
Digital Scales
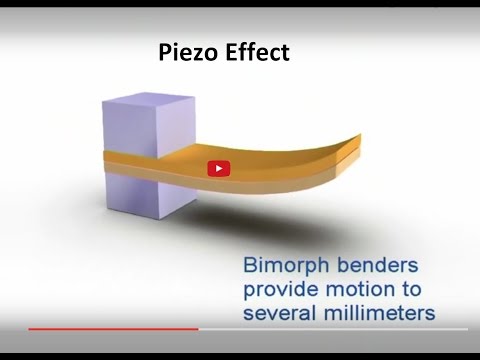
Many modern scales follow the same principle as spring scales, but instead of measuring the deformation directly, they measure an electric voltage created by a material in response to being deformed. Materials that produce voltages in response to deformation are known as piezoelectrics. As long as the relations between voltage and deformation and between deformation and applied force are both known, the scale can determine your weight by measuring a voltage.
An interesting aspect of the piezoelectric effect is reversibility, meaning that piezoelectric materials not only produce a voltage in response to deformation, they will also deform in response to an applied voltage, which allows for piezoelectric motors.
- OpenStax University Physics, University Physics Volume 1. OpenStax CNX. Sep 14, 2018 [1]http://cnx.org/contents/d50f6e32-0fda-46ef-a362-9bd36ca7c97d@11.28. ↵
- "Paula Khan" by Neal Snyder via Wikimedia Commons released in the public domain by U.S. Army Environmental Command ↵