6.2: Angular Acceleration
- Page ID
- 46185
Learning Objectives
- Describe uniform circular motion.
- Explain non-uniform circular motion.
- Explain what angular acceleration is.
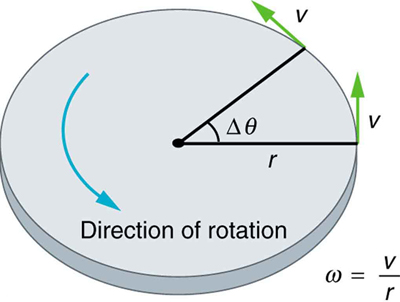
Previously, we looked at uniform circular motion, where an object moves in a circular path at a constant speed (but changing directions, so it undergoes centripetal acceleration). We can also describe this in terms of a rotation at a constant rate. For example, an object completing a circle every second can be said to rotate at a constant rate of 360 degrees per second about the center of the circle, since there are 360 degrees in one complete circle.
For the formulas and equations you will see in this chapter, we will introduce a mathematically convenient unit of angle called radians. An angular measure in radian is defined by the arc length covered by the angle divided by the radius of the circle that the arc length is part of. Do you see how, if the angular size remains the same, as we consider larger circles, with matching longer arc length, the ratio of arc length to the radius of the circle remains constant? Consider this example. The circumference \(S\) of a circle of radius \(r\) is given by \(S=2 \pi r\). So the angular size of a full circle is this circumference (a special kind of arc length) divided by the radius, or \(2 \pi\) (so you could say \(2 \pi\) radians is equal to 360 degrees).
So, imagine an object completing a uniform circular motion of radius \(r\) at speed \(v\), and let's say it takes time \(\Delta t\) to complete one full circle. Then using what we learned in kinematics, we know this holds:
\[v=\frac{\Delta s}{\Delta t}=\frac{2 \pi r}{\Delta t}, \label{1} \]
where \(\Delta s\) is the arc length, or the circumference, in this case. We can also describe this in terms of angular velocity, or the rate of change of angle,
\[\omega=\frac{\Delta \theta}{\Delta t}=\frac{2 \pi}{\Delta t}, \label{2} \]
where change of angle \(\Delta \theta\) in this case is the full circle, or \(2 \pi\) radians. We use \(\omega\) (lower-case omega) to denote angular velocity.
Carefully comparing Equation \(\eqref{1}\) with Equation \(\eqref{2}\), we see that following relationships hold:
\[v=r \omega \label{3} \]
and
\[\omega=\frac{v}{r}. \label{4} \]
We are going to use this relationship to relate linear motion with rotation (or angular motion) whenever necessary. A summary with figure is in Figure \(\PageIndex{1}\). In Figure \(\PageIndex{1}\), also note that, given the same angular velocity \(\omega\), an object at a larger radius has a larger linear speed (does this make intuitive sense?).
Angular velocity is not constant when a skater pulls in her arms (speeding up for some reason, which we'll look at why later), when a child starts up a merry-go-round from rest, or when a computer’s hard disk slows to a halt when switched off. In all these cases, there is an angular acceleration, in which \(\omega\) changes. The faster the change occurs, the greater the angular acceleration. Angular acceleration \(\alpha\) is defined as the rate of change of angular velocity. In equation form, angular acceleration is expressed as follows:
\[\alpha=\frac{\Delta \omega}{\Delta t}, \nonumber \]
where \(\Delta \omega\) is the change in angular velocity and \(\Delta t\) is the change in time. The units of angular acceleration are (rad/s)/s, or rad/s2. If \(\omega\) increases, then \(\alpha\) is positive. If \(\omega\) decreases, then \(\alpha\) is negative. Hopefully all this sounds rather familiar from a similar discussion in linear kinematics.
Example \(\PageIndex{1}\): Calculating the Angular Acceleration and Deceleration of a Bike Wheel
Suppose a teenager puts her bicycle on its back and starts the rear wheel spinning from rest to a final angular velocity of 250 rpm in 5.00 s. (a) Calculate the angular acceleration in rad/s2. (b) If she now slams on the brakes, causing an angular acceleration of –87.3 rad/s2, how long does it take the wheel to stop?
Strategy for (a)
The angular acceleration can be found directly from its definition in \(\alpha=\frac{\Delta \omega}{\Delta t}\) because the final angular velocity and time are given. We see that \(\Delta \omega\) is 250 rpm and \(\Delta t\) is 5.00 s.
Solution for (a)
Entering known information into the definition of angular acceleration, we get
\[\begin{aligned}
\alpha &=\frac{\Delta \omega}{\Delta t} \\
\\[0 pt] &=\frac{250 \mathrm{rpm}}{5.00 \mathrm{~s}}.
\end{aligned} \nonumber\]
Because \(\Delta \omega\) is in revolutions per minute (rpm) and we want the standard units of rad/s2 for angular acceleration, we need to convert \(\Delta \omega\) from rpm to rad/s:
\[\begin{aligned}
\Delta \omega &=250 \frac{\mathrm{rev}}{\min } \cdot \frac{2 \pi \mathrm{rad}}{\mathrm{rev}} \cdot \frac{1 \mathrm{~min}}{60 \mathrm{sec}} \\
&=26.2 \frac{\mathrm{rad}}{\mathrm{s}}.
\end{aligned} \nonumber\]
Entering this quantity into the expression for \(\alpha\), we get
\[\begin{aligned}
\alpha &=\frac{\Delta \omega}{\Delta t} \\
&=\frac{26.2 \mathrm{rad} / \mathrm{s}}{5.00 \mathrm{~s}} \\
&=5.24 \mathrm{rad} / \mathrm{s}^{2}.
\end{aligned} \nonumber\]
Strategy for (b)
In this part, we know the angular acceleration and the initial angular velocity. We can find the stoppage time by using the definition of angular acceleration and solving for \(\Delta t\), yielding
\[\Delta t=\frac{\Delta \omega}{\alpha}. \nonumber\]
Solution for (b)
Here the angular velocity decreases from 26.2 rad/s (250 rpm) to zero, so that \(\Delta \omega\) is –26.2 rad/s, and \(\alpha\) is given to be –87.3 rad/s2. Thus,
\[\begin{aligned}
\Delta t &=\frac{-26.2 \mathrm{rad} / \mathrm{s}}{-87.3 \mathrm{rad} / \mathrm{s}^{2}} \\
&=0.300 \mathrm{~s} .
\end{aligned} \nonumber\]
Discussion
Note that the angular acceleration as the girl spins the wheel is small and positive; it takes 5 s to produce an appreciable angular velocity. When she hits the brake, the angular acceleration is large and negative. The angular velocity quickly goes to zero. In both cases, the relationships are analogous to what happens with linear motion. For example, there is a large deceleration when you crash into a brick wall—the velocity change is large in a short time interval.
If the bicycle in the preceding example had been on its wheels instead of upside-down, it would first have accelerated along the ground and then come to a stop. This connection between circular motion and linear motion needs to be explored. For example, it would be useful to know how linear and angular acceleration are related. In circular motion, linear acceleration is tangent to the circle at the point of interest, as seen in Figure \(\PageIndex{2}\). Thus, linear acceleration is called tangential acceleration \(a_{\mathrm{t}}\). This is not to be confused with centripetal acceleration we covered earlier (see: Figure \(\PageIndex{3}\)).
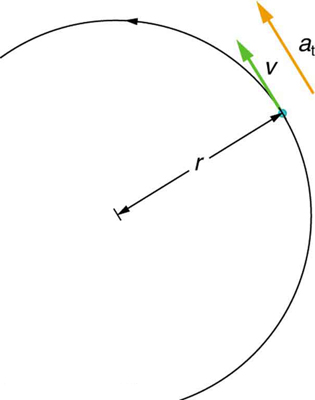
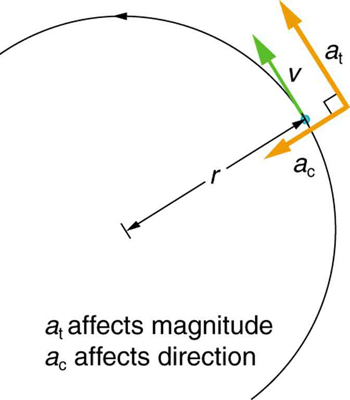
This tangential acceleration \(a_{\mathrm{t}}\) is related to angular acceleration \(\alpha\) in a similar way as how linear velocity is related to angular velocity. So, taking the cues from Equation \(\eqref{3}\) and Equation \(\eqref{4}\), tangential acceleration and angular acceleration are related by,
\[a_{\mathrm{t}}=r \alpha, \nonumber \]
and
\[\alpha=\frac{a_{\mathrm{t}}}{r}. \nonumber \]
These equations mean that linear acceleration and angular acceleration are directly proportional. The greater the angular acceleration is, the larger the linear (tangential) acceleration is, and vice versa. For example, the greater the angular acceleration of a car’s drive wheels, the greater the acceleration of the car. The radius also matters. For example, the smaller a wheel, the smaller its linear acceleration for a given angular acceleration \(\alpha\).
Example \(\PageIndex{2}\): Calculating the Angular Acceleration of a Motorcycle Wheel
A powerful motorcycle can accelerate from 0 to 30.0 m/s (about 108 km/h) in 4.20 s. What is the angular acceleration of its 0.320-m-radius wheels? (See Figure \(\PageIndex{4}\).)
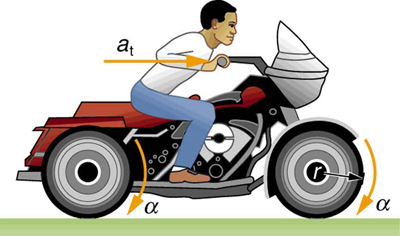
Strategy
We are given information about the linear velocities of the motorcycle. Thus, we can find its linear acceleration \(a_{\mathrm{t}}\). Then, the expression \(\alpha=\frac{a_{t}}{r}\) can be used to find the angular acceleration.
Solution
The linear acceleration is
\[\begin{aligned}
a_{\mathrm{t}} &=\frac{\Delta v}{\Delta t} \\
&=\frac{30.0 \mathrm{~m} / \mathrm{s}}{4.20 \mathrm{~s}} \\
&=7.14 \mathrm{~m} / \mathrm{s}^{2}.
\end{aligned} \nonumber\]
We also know the radius of the wheels. Entering the values for \(a_{\mathrm{t}}\) and \(r\) into \(\alpha=\frac{a_{t}}{r}\), we get
\[\begin{aligned}
\alpha &=\frac{a_{\mathrm{t}}}{r} \\
&=\frac{7.14 \mathrm{~m} / \mathrm{s}^{2}}{0.320 \mathrm{~m}} \\
&=22.3 \mathrm{rad} / \mathrm{s}^{2}.
\end{aligned} \nonumber\]
Discussion
Units of radians are dimensionless and appear in any relationship between angular and linear quantities.
So far, we have defined three rotational quantities— \(\theta\), \(\omega\), and \(\alpha\). These quantities are analogous to the translational quantities \(x\), \(v\), and \(a\). Table displays rotational quantities, the analogous translational quantities, and the relationships between them.
| Rotational | Translational | Relationship |
|---|---|---|
|
\(\theta\) |
\(x\) |
\(\theta=\frac{x}{r}\) |
|
\(\omega\) |
\(v\) |
\(\omega=\frac{v}{r}\) |
|
\(\alpha\) |
\(a\) |
\(\alpha=\frac{a_{t}}{r}\) |
MAKING CONNECTIONS: TAKE-HOME EXPERIMENT
Sit down with your feet on the ground on a chair that rotates. Lift one of your legs such that it is unbent (straightened out). Using the other leg, begin to rotate yourself by pushing on the ground. Stop using your leg to push the ground but allow the chair to rotate. From the origin where you began, sketch the angle, angular velocity, and angular acceleration of your leg as a function of time in the form of three separate graphs. Estimate the magnitudes of these quantities.
Exercise \(\PageIndex{1}\)
Angular acceleration is a vector, having both magnitude and direction. How do we denote its magnitude and direction? Illustrate with an example.
- Answer
-
The magnitude of angular acceleration is \(\alpha\) and its most common units are rad/s2. The direction of angular acceleration along a fixed axis is denoted by a + or a – sign, just as the direction of linear acceleration in one dimension is denoted by a + or a – sign. For example, consider a gymnast doing a forward flip. Her angular momentum would be parallel to the mat and to her left. The magnitude of her angular acceleration would be proportional to her angular velocity (spin rate) and her moment of inertia about her spin axis.
Section Summary
- Uniform circular motion is the motion with a constant angular velocity \(\omega=\frac{\Delta \theta}{\Delta t}\).
- In non-uniform circular motion, the velocity changes with time and the rate of change of angular velocity (i.e. angular acceleration) is \(\alpha=\frac{\Delta \omega}{\Delta t}\).
- Linear or tangential acceleration refers to changes in the magnitude of velocity but not its direction, given as \(a_{\mathrm{t}}=\frac{\Delta v}{\Delta t}\).
- Linear or tangential motion variables \(x\), \(v\), and \(a_{t}\) are proportional to the rotational quantities \(\theta\), \(\omega\), and \(\alpha\). They are also proportional to the radius \(r\) of the rotational motion.
Glossary
- angular acceleration
- the rate of change of angular velocity with time
- angular velocity
- the rate of change of angular position with time
- change in angular velocity
- the difference between final and initial values of angular velocity
- radian
- a unit of angular measure defined by the arc length covered by the angle divided by the radius of the circle that the arc length is part of; one full circle is \(2 \pi\) radians.
- tangential acceleration
- the acceleration in a direction tangent to the circle at the point of interest in circular motion