6.3: Dynamics of Rotational Motion- Rotational Inertia
- Page ID
- 46186
Learning Objectives
- Understand the relationship between torque, rotational inertia and angular acceleration.
- Study the turning effect of torque.
- Study the analogy between force and torque, mass and moment of inertia, and linear acceleration and angular acceleration.
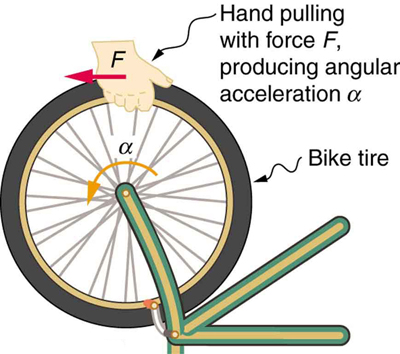
If you have ever spun a bike wheel or pushed a merry-go-round, you know that force is needed to change angular velocity as seen in Figure \(\PageIndex{1}\). In fact, your intuition is reliable in predicting many of the factors that are involved. For example, we know that a door opens slowly if we push too close to its hinges. Furthermore, we know that the more massive the door, the more slowly it opens. The first example implies that the farther the force is applied from the pivot, the greater the angular acceleration; another implication is that angular acceleration is inversely proportional to mass. These relationships should seem very similar to the familiar relationships among force, mass, and acceleration embodied in Newton’s second law of motion. There are, in fact, precise rotational analogs to both force and mass.
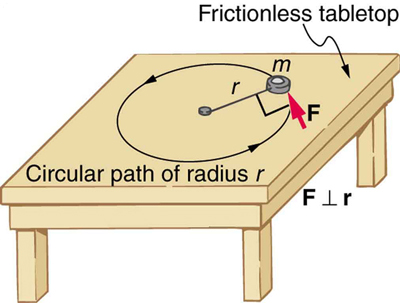
To develop the precise relationship among force, mass, radius, and angular acceleration, consider what happens if we exert a force \(F\) on a point mass \(m\) that is at a distance \(r\) from a pivot point, as shown in Figure \(\PageIndex{2}\). Because the force is perpendicular to \(r\), an acceleration \(a=\frac{F}{m}\) is obtained in the direction of \(F\). We can rearrange this equation such that \(F=m a\) and then look for ways to relate this expression to expressions for rotational quantities. We note that \(a=r \alpha\), and we substitute this expression into \(F=m a\), yielding
\[F=m r \alpha . \nonumber \]
The turning effectiveness of force is called torque. Intuitively, torque increases with a larger lever arm, or the perpendicular distance between the center of rotation and the point at which force is being applied (think of a see-saw; to balance the weight of a heavier child on one side with a lighter child on the other side, the lighter child needs to sit farther from the pivot point). So, torque is given by \(\tau=r F\). So, if we multiply both sides of the equation above by \(r\), we get torque on the left-hand side. That is,
\[r F=m r^{2} \alpha \nonumber \]
or
\[\tau=m r^{2} \alpha. \nonumber \]
This last equation is the rotational analog of Newton’s second law (\(F=m a\)), where torque is analogous to force, angular acceleration is analogous to translational acceleration, and \(m r^{2}\) is analogous to mass (or inertia). The quantity \(m r^{2}\) is called the rotational inertia or moment of inertia of a point mass \(m\) a distance \(r\) from the center of rotation.
MAKING CONNECTIONS: ROTATIONAL MOTION DYNAMICS
Dynamics for rotational motion is completely analogous to linear or translational dynamics. Dynamics is concerned with force and mass and their effects on motion. For rotational motion, we will find direct analogs to force and mass that behave just as we would expect from our earlier experiences.
Rotational Inertia and Moment of Inertia
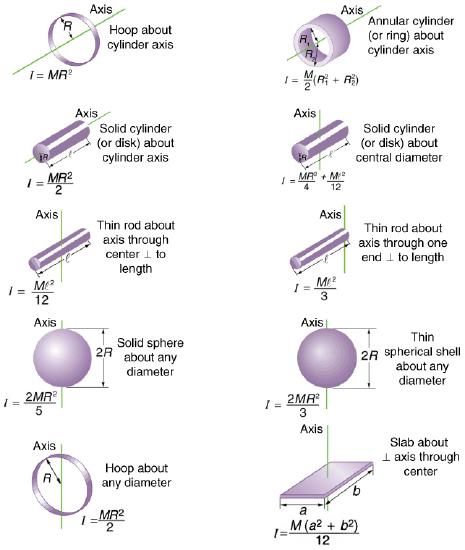
Before we can consider the rotation of anything other than a point mass like the one in Figure \(\PageIndex{2}\), we must extend the idea of rotational inertia to all types of objects. To expand our concept of rotational inertia, we define the moment of inertia \(I\) of an object to be the sum of \(m r^{2}\) for all the point masses of which it is composed. That is, \(I=\sum m r^{2}\). Here \(I\) is analogous to \(m\) in translational motion. Because of the distance \(r\), the moment of inertia for any object depends on the chosen axis. Actually, calculating \(I\) is beyond the scope of this text except for one simple case—that of a hoop, which has all its mass at the same distance from its axis. A hoop’s moment of inertia around its axis is therefore \(M R^{2}\), where \(M\) is its total mass and \(R\) its radius. (We use \(M\) and \(R\) for an entire object to distinguish them from \(m\) and \(r\) for point masses.) Figure \(\PageIndex{3}\) shows a variety of formulas of rotational inertia for many different shapes (deriving these formulas require calculus). For our purposes, it is good enough for you to see that rotational inertia is proportional to mass, and that it's proportional to size of object squared. Note that \ has units of mass multiplied by distance squared (\(\mathrm{kg} \cdot \mathrm{m}^{2}\)), as we might expect from its definition.
The general relationship among torque, moment of inertia, and angular acceleration is
\[\text { net } \tau=I \alpha \nonumber \]
or
\[\alpha=\frac{\text { net } \tau}{I}, \nonumber \]
where net \(\tau\) is the total torque from all forces relative to a chosen axis. For simplicity, we will only consider torques exerted by forces in the plane of the rotation. Such torques are either positive or negative and add like ordinary numbers. The relationship in \(\tau=I \alpha\), \(\alpha=\frac{\text { net } \tau}{I}\) is the rotational analog to Newton’s second law and is very generally applicable. This equation is actually valid for any torque, applied to any object, relative to any axis.
As we might expect, the larger the torque is, the larger the angular acceleration is. For example, the harder a child pushes on a merry-go-round, the faster it accelerates. Furthermore, the more massive a merry-go-round, the slower it accelerates for the same torque. The basic relationship between moment of inertia and angular acceleration is that the larger the moment of inertia, the smaller is the angular acceleration. But there is an additional twist. The moment of inertia depends not only on the mass of an object, but also on its distribution of mass relative to the axis around which it rotates. For example, it will be much easier to accelerate a merry-go-round full of children if they stand close to its axis than if they all stand at the outer edge. The mass is the same in both cases, but the moment of inertia is much larger when the children are at the edge.
TAKE-HOME EXPERIMENT
Cut out a circle that has about a 10 cm radius from stiff cardboard. Near the edge of the circle, write numbers 1 to 12 like hours on a clock face. Position the circle so that it can rotate freely about a horizontal axis through its center, like a wheel. (You could loosely nail the circle to a wall.) Hold the circle stationary and with the number 12 positioned at the top, attach a lump of blue putty (sticky material used for fixing posters to walls) at the number 3. How large does the lump need to be to just rotate the circle? Describe how you can change the moment of inertia of the circle. How does this change affect the amount of blue putty needed at the number 3 to just rotate the circle? Change the circle’s moment of inertia and then try rotating the circle by using different amounts of blue putty. Repeat this process several times.
MAKING CONNECTIONS
In statics, the net torque is zero, and there is no angular acceleration. In rotational motion, net torque is the cause of angular acceleration, exactly as in Newton’s second law of motion for rotation.
Exercise \(\PageIndex{1}\)
Torque is the analog of force and moment of inertia is the analog of mass. Force and mass are physical quantities that depend on only one factor. For example, mass is related solely to the numbers of atoms of various types in an object. Are torque and moment of inertia similarly simple?
- Answer
-
No. Torque depends on three factors: force magnitude, force direction, and point of application. Moment of inertia depends on both mass and its distribution relative to the axis of rotation. So, while the analogies are precise, these rotational quantities depend on more factors.
Section Summary
- The farther the force is applied from the pivot, the greater is the angular acceleration; angular acceleration is inversely proportional to mass.
- The torque applied on an object is given by lever arm times the applied force: \(\tau=r F\).
- Using the torque, we can discover the rotational version of Newton's Second Law. It says \(\tau=I \alpha\), where \(I\) is rotational inertia, defined for a point mass moving in a circle of radius \(r\) as \(I=m r^{2}\).
- The formula for rotational inertia of an extended body can be complicated. But they are all proportional to the mass of the object and proportional to the square of the size of the object.
Glossary
- torque
- the turning effectiveness of a force
- lever arm
- the perpendicular distance between the center of rotation and the point at which force is being applied
- rotational inertia
- resistance to change of angular velocity; also called moment of inertia; for a point mass, \(I=m r^{2}\)