6.4: Rotational Kinetic Energy

Learning Objectives

• Guess the equation for rotational kinetic energy by analogy.
• Calculate rotational kinetic energy.

In this module, we will learn about work and energy associated with rotational motion. Figure \(\PageIndex{1}\) shows a worker using an electric grindstone propelled by a motor. Sparks are flying, and noise and vibration are created as layers of steel are pared from the pole. The stone continues to turn even after the motor is turned off, but it is eventually brought to a stop by friction. Clearly, the motor had to work to get the stone spinning. This work went into heat, light, sound, vibration, and considerable rotational kinetic energy.

Figure \(\PageIndex{1}\): The motor works in spinning the grindstone, giving it rotational kinetic energy. That energy is then converted to heat, light, sound, and vibration. (credit: U.S. Navy photo by Mass Communication Specialist Seaman Zachary David Bell)

Instead of deriving the formula for rotational kinetic energy by calculating the work done by torque on a rotating object, we can simply guess the correct formula by analogy. We know the kinetic energy in linear, or translational motion, \(\mathrm{KE}=\frac{1}{2} m v^{2}\). We can find the rotational version of kinetic energy by replacing mass \(m\) with rotational version of mass, rotational inertia \(I\), and by replacing speed \(v\) with rotational speed \(\omega\). Rotational speed is measured in units of radians per second. With these replacements, we get the formula for rotational kinetic energy,

\[\mathrm{KE}_{\mathrm{rot}}=\frac{1}{2} I \omega^{2}. \nonumber \]

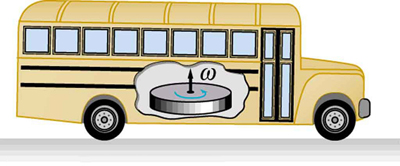
Rotational kinetic energy has important effects. Flywheels, for example, can be used to store large amounts of rotational kinetic energy in a vehicle, as seen in Figure \(\PageIndex{2}\).

Figure \(\PageIndex{2}\): Experimental vehicles, such as this bus, have been constructed in which rotational kinetic energy is stored in a large flywheel. When the bus goes down a hill, its transmission converts its gravitational potential energy into \(\mathrm{KE}_{\text {rot }}\). It can also convert translational kinetic energy, when the bus stops, into \(\mathrm{KE}_{\text {rot }}\). The flywheel’s energy can then be used to accelerate, to go up another hill, or to keep the bus from going against friction.

Helicopter pilots are quite familiar with rotational kinetic energy. They know, for example, that a point of no return will be reached if they allow their blades to slow below a critical angular velocity during flight. The blades lose lift, and it is impossible to immediately get the blades spinning fast enough to regain it. Rotational kinetic energy must be supplied to the blades to get them to rotate faster, and enough energy cannot be supplied in time to avoid a crash. Because of weight limitations, helicopter engines are too small to supply both the energy needed for lift and to replenish the rotational kinetic energy of the blades once they have slowed down. The rotational kinetic energy is put into them before takeoff and must not be allowed to drop below this crucial level. One possible way to avoid a crash is to use the gravitational potential energy of the helicopter to replenish the rotational kinetic energy of the blades by losing altitude and aligning the blades so that the helicopter is spun up in the descent. Of course, if the helicopter’s altitude is too low, then there is insufficient time for the blade to regain lift before reaching the ground.

Example \(\PageIndex{1}\): Calculating Helicopter Energies

A typical small rescue helicopter, similar to the one in Figure \(\PageIndex{3}\), has four blades, each is 4.00 m long and has a mass of 50.0 kg. The blades can be approximated as thin rods that rotate about one end of an axis perpendicular to their length. The helicopter has a total loaded mass of 1000 kg. (a) Calculate the rotational kinetic energy in the blades when they rotate at 300 rpm. (b) Calculate the translational kinetic energy of the helicopter when it flies at 20.0 m/s, and compare it with the rotational energy in the blades. (c) To what height could the helicopter be raised if all of the rotational kinetic energy could be used to lift it?

Strategy

Rotational and translational kinetic energies can be calculated from their definitions. The last part of the problem relates to the idea that energy can change form, in this case from rotational kinetic energy to gravitational potential energy.

Solution for (a)

The rotational kinetic energy is

\[\mathrm{KE}_{\mathrm{rot}}=\frac{1}{2} I \omega^{2}. \nonumber\]

We must convert the angular velocity to radians per second and calculate the moment of inertia before we can find \(\mathrm{KE}_{\mathrm{rot}}\). The angular velocity \(\omega\) is

\[\omega=\frac{300 \mathrm{rev}}{1.00 \mathrm{~min}} \cdot \frac{2 \pi \mathrm{rad}}{1 \mathrm{rev}} \cdot \frac{1.00 \mathrm{~min}}{60.0 \mathrm{~s}}=31.4 \frac{\mathrm{rad}}{\mathrm{s}}. \nonumber\]

The moment of inertia of one blade will be that of a thin rod rotated about its end, \(I_{\mathrm{rod}}=\frac{1}{3} M \ell^{2}\). The total \(I\) is four times this moment of inertia, because there are four blades. Thus,

\[I=4 \frac{M \ell^{2}}{3}=4 \times \frac{(50.0 \mathrm{~kg})(4.00 \mathrm{~m})^{2}}{3}=1067 \mathrm{~kg} \cdot \mathrm{m}^{2}. \nonumber\]

Entering \(\omega\) and \(I\) into the expression for rotational kinetic energy gives

\[\begin{aligned}
\mathrm{KE}_{\mathrm{rot}} &=0.5\left(1067 \mathrm{~kg} \cdot \mathrm{m}^{2}\right)(31.4 \mathrm{rad} / \mathrm{s})^{2} \\
&=5.26 \times 10^{5} \mathrm{~J}
\end{aligned} \nonumber\]

Solution for (b)

Entering the given values of mass and velocity into formula for translational kinetic energy, we obtain

\[\mathrm{KE}_{\text {trans }}=\frac{1}{2} m v^{2}=(0.5)(1000 \mathrm{~kg})(20.0 \mathrm{~m} / \mathrm{s})^{2}=2.00 \times 10^{5} \mathrm{~J}. \nonumber\]

To compare kinetic energies, we take the ratio of translational kinetic energy to rotational kinetic energy. This ratio is

\[\frac{2.00 \times 10^{5} \mathrm{~J}}{5.26 \times 10^{5} \mathrm{~J}}=0.380. \nonumber\]

Solution for (c)

At the maximum height, all rotational kinetic energy will have been converted to gravitational energy. To find this height, we equate those two energies:

\[\mathrm{KE}_{\text {rot }}=\mathrm{PE}_{\text {grav }} \nonumber\]

or

\[\frac{1}{2} I \omega^{2}=m g h. \nonumber\]

We now solve for \(h\) and substitute known values into the resulting equation

\[h=\frac{\frac{1}{2} I \omega^{2}}{m g}=\frac{5.26 \times 10^{5} \mathrm{~J}}{(1000 \mathrm{~kg})\left(9.80 \mathrm{~m} / \mathrm{s}^{2}\right)}=53.7 \mathrm{~m}. \nonumber\]

Discussion

The ratio of translational energy to rotational kinetic energy is only 0.380. This ratio tells us that most of the kinetic energy of the helicopter is in its spinning blades—something you probably would not suspect. The 53.7 m height to which the helicopter could be raised with the rotational kinetic energy is also impressive, again emphasizing the amount of rotational kinetic energy in the blades.

Figure \(\PageIndex{3}\): The first image shows how helicopters store large amounts of rotational kinetic energy in their blades. This energy must be put into the blades before takeoff and maintained until the end of the flight. The engines do not have enough power to simultaneously provide lift and put significant rotational energy into the blades. The second image shows a helicopter from the Auckland Westpac Rescue Helicopter Service. Over 50,000 lives have been saved since its operations beginning in 1973. Here, a water rescue operation is shown. (credit: 111 Emergency, Flickr)

How Thick Is the Soup? Or Why Don’t All Objects Roll Downhill at the Same Rate?

One of the quality controls in a tomato soup factory consists of rolling filled cans down a ramp. If they roll too fast, the soup is too thin. Why should cans of identical size and mass roll down an incline at different rates? And why should the thickest soup roll the slowest?

The easiest way to answer these questions is to consider energy. Suppose each can starts down the ramp from rest. Each can starting from rest means each starts with the same gravitational potential energy \(\mathrm{PE}_{\text {grav }}\), which is converted entirely to KE, provided each rolls without slipping. KE, however, can take the form of \(\mathrm{KE}_{\text {trans }}\) or \(\mathrm{KE}_{\text {rot }}\), and total KE is the sum of the two. If a can rolls down a ramp, it puts part of its energy into rotation, leaving less for translation. Thus, the can goes slower than it would if it slid down. Furthermore, the thin soup does not rotate, whereas the thick soup does, because it sticks to the can. The thick soup thus puts more of the can’s original gravitational potential energy into rotation than the thin soup, and the can rolls more slowly, as seen in Figure \(\PageIndex{4}\).

Figure \(\PageIndex{4}\): Three cans of soup with identical masses race down an incline. The first can has a low friction coating and does not roll but just slides down the incline. It wins because it converts its entire PE into translational KE. The second and third cans both roll down the incline without slipping. The second can contains thin soup and comes in second because part of its initial PE goes into rotating the can (but not the thin soup). The third can contains thick soup. It comes in third because the soup rotates along with the can, taking even more of the initial PE for rotational KE, leaving less for translational KE.

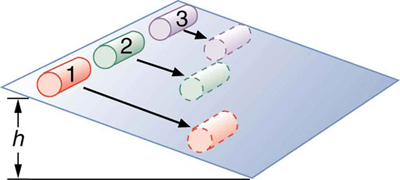
Assuming no losses due to friction, there is only one force doing work—gravity. Therefore the total work done is the change in kinetic energy. As the cans start moving, the potential energy is changing into kinetic energy. Conservation of energy gives

\[\mathrm{PE}_{\mathrm{i}}=\mathrm{KE}_{\mathrm{f}}. \nonumber \]

More specifically,

\[\mathrm{PE}_{\text {grav }}=\mathrm{KE}_{\text {trans }}+\mathrm{KE}_{\mathrm{rot}} \nonumber \]

or

\[m g h=\frac{1}{2} m v^{2}+\frac{1}{2} I \omega^{2}. \nonumber \]

So, the initial \(mgh\) is divided between translational kinetic energy and rotational kinetic energy; and the greater \(I\) is, the less energy goes into translation. If the can slides down without friction, then \(ω=0\) and all the energy goes into translation; thus, the can goes faster.

TAKE-HOME EXPERIMENT

Locate several cans each containing a different type of food (for example, canned soup with different kinds of soup). First, predict which can will win the race down an inclined plane and explain why. See if your prediction is correct. A good contrast can be obtained between a thick soup concentrate (for example, condensed cream of mushroom) and a thin soup (for example, chicken noodle soup). If you feel adventurous, try other foods, such as canned corn or peas; try predicting how these would compare to, for example, condensed cream of mushroom can in the race down an inclined plane.

Example \(\PageIndex{2}\): Calculating the Speed of a Cylinder Rolling Down an Incline

Calculate the final speed of a solid cylinder that rolls down a 2.00-m-high incline. The cylinder starts from rest, has a mass of 0.750 kg, and has a radius of 4.00 cm.

Strategy

We can solve for the final velocity using conservation of energy, but we must first express rotational quantities in terms of translational quantities to end up with v as the only unknown.

Solution

Conservation of energy for this situation is written as described above:

\[m g h=\frac{1}{2} m v^{2}+\frac{1}{2} I \omega^{2}. \nonumber\]

Before we can solve for \(v\) , we must look up an expression for \(I\) for a solid disk: \(I_{\text {disk }}=\frac{1}{2} M \ell^{2}\). Because \(v\) and \(\omega\) are related (note here that the cylinder is rolling without slipping), we must also substitute the relationship \(\omega=v / R\) into the expression. These substitutions yield

\[m g h=\frac{1}{2} m v^{2}+\frac{1}{2}\left(\frac{1}{2} m R^{2}\right)\left(\frac{v^{2}}{R^{2}}\right). \nonumber\]

Interestingly, the cylinder’s radius \(R\) and mass \(m\) cancel, yielding

\[g h=\frac{1}{2} v^{2}+\frac{1}{4} v^{2}=\frac{3}{4} v^{2}. \nonumber\]

Solving algebraically, the equation for the final velocity \(v\) gives

\[v=\left(\frac{4 g h}{3}\right)^{1 / 2}. \nonumber\]

Substituting known values into the resulting expression yields

\[v=\left[\frac{4\left(9.80 \mathrm{~m} / \mathrm{s}^{2}\right)(2.00 \mathrm{~m})}{3}\right]^{1 / 2}=5.11 \mathrm{~m} / \mathrm{s}. \nonumber\]

Discussion

Because \(m\) and \(R\) cancel, the result \(v=\left(\frac{4}{3} g h\right)^{1 / 2}\) is valid for any solid cylinder, implying that all solid cylinders will roll down an incline at the same rate independent of their masses and sizes. (Rolling cylinders down inclines is what Galileo actually did to show that objects fall at the same rate independent of mass.) Note that if the cylinder slid without friction down the incline without rolling, then the entire gravitational potential energy would go into translational kinetic energy. Thus, \(\frac{1}{2} m v^{2}=m g h\) and \(v=(2 g h)^{1 / 2}\), which is 22% greater than \((4 g h / 3)^{1 / 2}\). That is, the cylinder would go faster at the bottom.

Exercise \(\PageIndex{1}\)

Analogy of Rotational and Translational Kinetic Energy

Is rotational kinetic energy completely analogous to translational kinetic energy? What, if any, are their differences? Give an example of each type of kinetic energy.

Answer

Yes, rotational and translational kinetic energy are exact analogs. They both are the energy of motion involved with the coordinated (non-random) movement of mass relative to some reference frame. The only difference between rotational and translational kinetic energy is that translational is straight line motion while rotational is not. An example of both kinetic and translational kinetic energy is found in a bike tire while being ridden down a bike path. The rotational motion of the tire means it has rotational kinetic energy while the movement of the bike along the path means the tire also has translational kinetic energy. If you were to lift the front wheel of the bike and spin it while the bike is stationary, then the wheel would have only rotational kinetic energy relative to the Earth.

Section Summary

• The rotational kinetic energy \(\mathrm{KE}_{\text {rot }}\) for an object with a moment of inertia \(I\) and an angular velocity \(\omega\) is given by

  \[\mathrm{KE}_{\mathrm{rot}}=\frac{1}{2} I \omega^{2}. \nonumber\]

• Helicopters store large amounts of rotational kinetic energy in their blades. This energy must be put into the blades before takeoff and maintained until the end of the flight. The engines do not have enough power to simultaneously provide lift and put significant rotational energy into the blades.
• Work and energy in rotational motion are completely analogous to work and energy in translational motion.

Glossary

rotational kinetic energy

the kinetic energy due to the rotation of an object. This is part of its total kinetic energy