8.13: Entropy and the Second Law of Thermodynamics- Disorder and the Unavailability of Energy

Learning Objectives

• Define entropy and calculate the increase of entropy in a system with reversible and irreversible processes.
• Calculate the increasing disorder of a system.

Figure \(\PageIndex{1}\): The ice in this drink is slowly melting. Eventually the liquid will reach thermal equilibrium, as predicted by the second law of thermodynamics. (credit: Jon Sullivan, PDPhoto.org)

There is yet another way of expressing the second law of thermodynamics. This version relates to a concept called entropy. By examining it, we shall see that the directions associated with the second law—heat transfer from hot to cold, for example—are related to the tendency in nature for systems to become disordered and for less energy to be available for use as work. The entropy of a system can in fact be shown to be a measure of its disorder and of the unavailability of energy to do work.

MAKING CONNECTIONS: ENTROPY, ENERGY, AND WORK

Recall that the simple definition of energy is the ability to do work. Entropy is a measure of how much energy is not available to do work. Although all forms of energy are interconvertible, and all can be used to do work, it is not always possible, even in principle, to convert the entire available energy into work. That unavailable energy is of interest in thermodynamics, because the field of thermodynamics arose from efforts to convert heat to work.

We can see how entropy is defined by recalling our discussion of the Carnot engine. We noted that for a Carnot cycle, and hence for any reversible processes, \(Q_{\mathrm{c}} / Q_{\mathrm{h}}=T_{\mathrm{c}} / T_{\mathrm{h}}\). Rearranging terms yields

\[\frac{Q_{\mathrm{c}}}{T_{\mathrm{c}}}=\frac{Q_{\mathrm{h}}}{T_{\mathrm{h}}} \nonumber \]

for any reversible process. \(Q_{\mathrm{c}}\) and \(Q_{\mathrm{h}}\) are absolute values of the heat transfer at temperatures \(T_{\mathrm{c}}\) and \(T_{\mathrm{h}}\), respectively. This ratio of \(Q / T\) is defined to be the change in entropy \(\Delta S\) for a reversible process,

\[\Delta S=\left(\frac{Q}{T}\right)_{\mathrm{rev}}, \nonumber \]

where \(Q\) is the heat transfer, which is positive for heat transfer into and negative for heat transfer out of, and \(T\) is the absolute temperature at which the reversible process takes place. The SI unit for entropy is joules per kelvin (J/K). If temperature changes during the process, then it is usually a good approximation (for small changes in temperature) to take \(T\) to be the average temperature, avoiding the need to use integral calculus to find \(\Delta S\).

The definition of \(\Delta S\) is strictly valid only for reversible processes, such as used in a Carnot engine. However, we can find \(\Delta S\) precisely even for real, irreversible processes. The reason is that the entropy \(S\) of a system, like internal energy \(U\), depends only on the state of the system and not how it reached that condition. Entropy is a property of state. Thus the change in entropy \(\Delta S\) of a system between state 1 and state 2 is the same no matter how the change occurs. We just need to find or imagine a reversible process that takes us from state 1 to state 2 and calculate \(\Delta S\) for that process. That will be the change in entropy for any process going from state 1 to state 2. (See Figure \(\PageIndex{2}\).)

Figure \(\PageIndex{2}\): When a system goes from state 1 to state 2, its entropy changes by the same amount \(\Delta S\), whether a hypothetical reversible path is followed or a real irreversible path is taken.

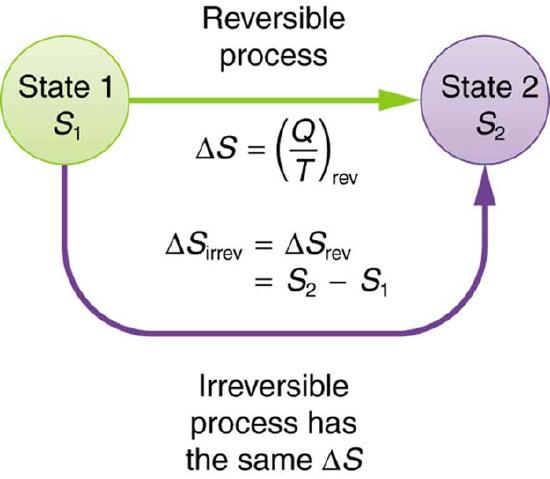
Now let us take a look at the change in entropy of a Carnot engine and its heat reservoirs for one full cycle. The hot reservoir has a loss of entropy \(\Delta S_{\mathrm{h}}=-Q_{\mathrm{h}} / T_{\mathrm{h}}\), because heat transfer occurs out of it (remember that when heat transfers out, then \(Q\) has a negative sign). The cold reservoir has a gain of entropy \(\Delta S_{\mathrm{c}}=Q_{\mathrm{c}} / T_{\mathrm{c}}\), because heat transfer occurs into it. (We assume the reservoirs are sufficiently large that their temperatures are constant.) So the total change in entropy is

\[\Delta S_{\text {tot }}=\Delta S_{\mathrm{h}}+\Delta S_{\mathrm{c}} \nonumber \]

Thus, since we know that \(Q_{\mathrm{h}} / T_{\mathrm{h}}=Q_{\mathrm{c}} / T_{\mathrm{c}}\) for a Carnot engine,

\[\Delta S_{\mathrm{tot}}=-\frac{Q_{\mathrm{h}}}{T_{\mathrm{h}}}+\frac{Q_{\mathrm{c}}}{T_{\mathrm{c}}}=0. \nonumber \]

This result, which has general validity, means that the total change in entropy for a system in any reversible process is zero.

The entropy of various parts of the system may change, but the total change is zero. Furthermore, the system does not affect the entropy of its surroundings, since heat transfer between them does not occur. Thus the reversible process changes neither the total entropy of the system nor the entropy of its surroundings. Sometimes this is stated as follows: Reversible processes do not affect the total entropy of the universe. Real processes are not reversible, though, and they do change total entropy. We can, however, use hypothetical reversible processes to determine the value of entropy in real, irreversible processes. The following example illustrates this point.

Example \(\PageIndex{1}\): Entropy Increases in an Irreversible (Real) Process

Spontaneous heat transfer from hot to cold is an irreversible process. Calculate the total change in entropy if 4000 J of heat transfer occurs from a hot reservoir at \(T_{\mathrm{h}}=600 \mathrm{~K} \ \left(327^{\circ} \mathrm{C}\right)\) to a cold reservoir at \(T_{\mathrm{c}}=250 \mathrm{~K} \ \left(-23^{\circ} \mathrm{C}\right)\), assuming there is no temperature change in either reservoir. (See Figure \(\PageIndex{3}\).)

Strategy

How can we calculate the change in entropy for an irreversible process when \(\Delta S_{\mathrm{tot}}=\Delta S_{\mathrm{h}}+\Delta S_{\mathrm{c}}\) is valid only for reversible processes? Remember that the total change in entropy of the hot and cold reservoirs will be the same whether a reversible or irreversible process is involved in heat transfer from hot to cold. So we can calculate the change in entropy of the hot reservoir for a hypothetical reversible process in which 4000 J of heat transfer occurs from it; then we do the same for a hypothetical reversible process in which 4000 J of heat transfer occurs to the cold reservoir. This produces the same changes in the hot and cold reservoirs that would occur if the heat transfer were allowed to occur irreversibly between them, and so it also produces the same changes in entropy.

Solution

We now calculate the two changes in entropy using \(\Delta S_{\text {tot }}=\Delta S_{\mathrm{h}}+\Delta S_{\mathrm{c}}\). First, for the heat transfer from the hot reservoir,

\[\Delta S_{\mathrm{h}}=\frac{-Q_{\mathrm{h}}}{T_{\mathrm{h}}}=\frac{-4000 \mathrm{~J}}{600 \mathrm{~K}}=-6.67 \mathrm{~J} / \mathrm{K}. \nonumber\]

And for the cold reservoir,

\[\Delta S_{\mathrm{c}}=\frac{Q_{\mathrm{c}}}{T_{\mathrm{c}}}=\frac{4000 \mathrm{~J}}{250 \mathrm{~K}}=16.0 \mathrm{~J} / \mathrm{K}. \nonumber\]

Thus the total is

\[\begin{aligned}
\Delta S_{\text {tot }} &=\Delta S_{\mathrm{h}}+\Delta S_{\mathrm{c}} \\
&=(-6.67+16.0) \mathrm{J} / \mathrm{K} \\
&=9.33 \mathrm{~J} / \mathrm{K}.
\end{aligned} \nonumber\]

Discussion

There is an increase in entropy for the system of two heat reservoirs undergoing this irreversible heat transfer. We will see that this means there is a loss of ability to do work with this transferred energy. Entropy has increased, and energy has become unavailable to do work.

Figure \(\PageIndex{3}\): (a) Heat transfer from a hot object to a cold one is an irreversible process that produces an overall increase in entropy. (b) The same final state and, thus, the same change in entropy is achieved for the objects if reversible heat transfer processes occur between the two objects whose temperatures are the same as the temperatures of the corresponding objects in the irreversible process.

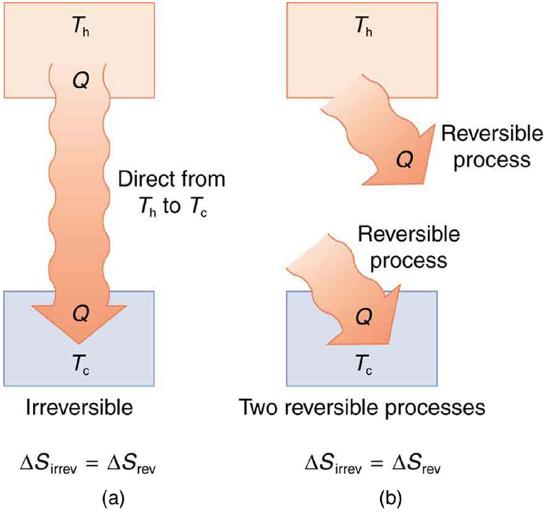
It is reasonable that entropy increases for heat transfer from hot to cold. Since the change in entropy is \(Q / T\), there is a larger change at lower temperatures. The decrease in entropy of the hot object is therefore less than the increase in entropy of the cold object, producing an overall increase, just as in the previous example. This result is very general:

There is an increase in entropy for any system undergoing an irreversible process.

With respect to entropy, there are only two possibilities: entropy is constant for a reversible process, and it increases for an irreversible process. There is a fourth version of the second law of thermodynamics stated in terms of entropy:

The total entropy of a system either increases or remains constant in any process; it never decreases.

For example, heat transfer cannot occur spontaneously from cold to hot, because entropy would decrease.

Entropy is very different from energy. Entropy is not conserved but increases in all real processes. Reversible processes (such as in Carnot engines) are the processes in which the most heat transfer to work takes place and are also the ones that keep entropy constant. Thus we are led to make a connection between entropy and the availability of energy to do work.

Order to Disorder

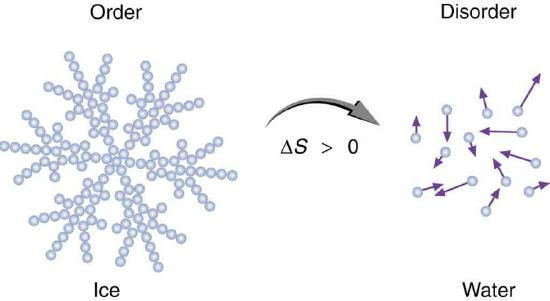
Entropy is related not only to the unavailability of energy to do work—it is also a measure of disorder. This notion was initially postulated by Ludwig Boltzmann in the 1800s. For example, melting a block of ice means taking a highly structured and orderly system of water molecules and converting it into a disorderly liquid in which molecules have no fixed positions. (See Figure \(\PageIndex{4}\).) There is a large increase in entropy in the process, as seen in the following example.

Example \(\PageIndex{2}\): Entropy Associated with Disorder

Find the increase in entropy of 1.00 kg of ice originally at \(0^{\circ} \mathrm{C}\) that is melted to form water at \(0^{\circ} \mathrm{C}\).

Strategy

As before, the change in entropy can be calculated from the definition of \(\Delta S\) once we find the energy \(Q\) needed to melt the ice.

Solution

The change in entropy is defined as:

\[\Delta S=\frac{Q}{T}. \nonumber\]

Here \(Q\) is the heat transfer necessary to melt 1.00 kg of ice and is given by

\[Q=m L_{\mathrm{f}}, \nonumber\]

where \(m\) is the mass and \(L_{\mathrm{f}}\) is the latent heat of fusion. \(L_{\mathrm{f}}=334 \mathrm{~kJ} / \mathrm{kg}\) for water, so that

\[Q=(1.00 \mathrm{~kg})(334 \mathrm{~kJ} / \mathrm{kg})=3.34 \times 10^{5} \mathrm{~J}. \nonumber\]

Now the change in entropy is positive, since heat transfer occurs into the ice to cause the phase change; thus,

\[\Delta S=\frac{Q}{T}=\frac{3.34 \times 10^{5} \mathrm{~J}}{T}. \nonumber\]

\(T\) is the melting temperature of ice. That is, \(T=0^{\circ} \mathrm{C}=273 \mathrm{~K}\). So the change in entropy is

\[\begin{aligned}
\Delta S &=\frac{3.34 \times 10^{5} \mathrm{~J}}{273 \mathrm{~K}} \\
&=1.22 \times 10^{3} \mathrm{~J} / \mathrm{K}.
\end{aligned} \nonumber\]

Discussion

This is a significant increase in entropy accompanying an increase in disorder.

Figure \(\PageIndex{4}\): When ice melts, it becomes more disordered and less structured. The systematic arrangement of molecules in a crystal structure is replaced by a more random and less orderly movement of molecules without fixed locations or orientations. Its entropy increases because heat transfer occurs into it. Entropy is a measure of disorder.

In another easily imagined example, suppose we mix equal masses of water originally at two different temperatures, say \(20.0^{\circ} \mathrm{C}\) and \(40.0^{\circ} \mathrm{C}\). The result is water at an intermediate temperature of \(30.0^{\circ} \mathrm{C}\). Three outcomes have resulted: entropy has increased, some energy has become unavailable to do work, and the system has become less orderly. Let us think about each of these results.

First, entropy has increased for the same reason that it did in the example above. Mixing the two bodies of water has the same effect as heat transfer from the hot one and the same heat transfer into the cold one. The mixing decreases the entropy of the hot water but increases the entropy of the cold water by a greater amount, producing an overall increase in entropy.

Second, once the two masses of water are mixed, there is only one temperature—you cannot run a heat engine with them. The energy that could have been used to run a heat engine is now unavailable to do work.

Third, the mixture is less orderly, or to use another term, less structured. Rather than having two masses at different temperatures and with different distributions of molecular speeds, we now have a single mass with a uniform temperature.

These three results—entropy, unavailability of energy, and disorder—are not only related but are in fact essentially equivalent.

Section Summary

• Entropy is the loss of energy available to do work.
• Another form of the second law of thermodynamics states that the total entropy of a system either increases or remains constant; it never decreases.
• Change of entropy is zero in a reversible process; it increases in an irreversible process.
• Entropy is also associated with the tendency toward disorder in an isolated system.

Glossary

entropy

a measurement of a system's disorder and its inability to do work in a system

change in entropy

the ratio of heat transfer to temperature \(Q/T\)

second law of thermodynamics stated in terms of entropy

the total entropy of a system either increases or remains constant; it never decreases