12.4: The Wave Nature of Matter

Learning Objectives

• Describe de Broglie wavelength of particles.
• Explain wave-particle duality of nature.

De Broglie Wavelength

In the photoelectric effect, we have seen that light, classically understood as waves, behaves like particles sometimes. In 1923 a French physics graduate student named Prince Louis-Victor de Broglie (1892–1987) made a radical proposal based on the hope that nature is symmetric, suggesting that not only EM radiation has both particle and wave properties but that this dual-nature might be universal to all particles. De Broglie’s suggestion, made as part of his doctoral thesis, was so radical that it was greeted with some skepticism. A copy of his thesis was sent to Einstein, who said it was not only probably correct, but that it might be of fundamental importance. With the support of Einstein and a few other prominent physicists, de Broglie was awarded his doctorate.

De Broglie took both relativity and quantum mechanics into account to develop the proposal that all particles have a wavelength, given by

\[\lambda=\frac{h}{p} \text { (matter and photons), } \nonumber \]

where \(h\) is Planck’s constant and \(p\) is momentum. This is defined to be the de Broglie wavelength. This is consistent with the expression for energy of a photon, \(E=h f\). In relativity, energy of a massless particle like a photon is related to momentum by \(E=p c\), where \(c\) is speed of light (contrast this with nonrelativistic kinetic energy of particles of mass \(m\), \(\mathrm{KE}=p^{2} / 2 m\); check the units for yourself). From the wave relationship between wave speed, wavelength, and frequency, we have, for photons, \(c=\lambda f\). Plugging in these \(E\) and \(f\) into the photon energy from the photoelectric effect, we get, \(p c=h c / \lambda\), and cancelling out \(c\) from both sides gives the same expression as de Broglie wavelength.

The hallmark of a wave is interference. If matter is a wave, then it must exhibit constructive and destructive interference. Why isn’t this ordinarily observed? The answer is that in order to see significant interference effects, a wave must interact with an object about the same size as its wavelength. Since \(h\) is very small, \(\lambda\) is also small, especially for macroscopic objects. A 3-kg bowling ball moving at 10 m/s, for example, has

\[\lambda=h / p=\left(6.63 \times 10^{-34} \mathrm{~J} \cdot \mathrm{s}\right) /[(3 \mathrm{~kg})(10 \mathrm{~m} / \mathrm{s})]=2 \times 10^{-35} \mathrm{~m}. \nonumber\]

This means that to see its wave characteristics, the bowling ball would have to interact with something about \(10^{-35} \mathrm{~m}\) in size—far smaller than anything known. When waves interact with objects much larger than their wavelength, they show negligible interference effects and move in straight lines (such as light rays in geometric optics). To obtain longer wavelengths and make wave nature of matter readily apparent, we need smaller momentum, \(p\), and this is easier to achieve in electrons, the lightest common matter particle we know.

American physicists Clinton J. Davisson and Lester H. Germer in 1925 and, independently, British physicist G. P. Thomson (son of J. J. Thomson, discoverer of the electron) in 1926 scattered electrons from crystals and found diffraction patterns. These patterns are exactly consistent with interference of electrons having the de Broglie wavelength and are somewhat analogous to light interacting with a diffraction grating. (See Figure \(\PageIndex{1}\).)

CONNECTIONS: WAVES

All microscopic particles, whether massless, like photons, or having mass, like electrons, have wave properties. The relationship between momentum and wavelength is fundamental for all particles.

De Broglie’s proposal of a wave nature for all particles initiated a remarkably productive era in which the foundations for quantum mechanics were laid. In 1926, the Austrian physicist Erwin Schrödinger (1887–1961) published four papers in which the wave nature of particles was treated explicitly with wave equations. At the same time, many others began important work. Among them was German physicist Werner Heisenberg (1901–1976) who, among many other contributions to quantum mechanics, formulated a mathematical treatment of the wave nature of matter that used matrices rather than wave equations. De Broglie’s work—recognition of the universal nature of wave-particle duality, as expressed in de Broglie wavelength—was a watershed for the development of quantum mechanics. De Broglie was awarded the Nobel Prize in 1929 for his vision, as were Davisson and G. P. Thomson in 1937 for their experimental verification of de Broglie’s hypothesis.

Figure \(\PageIndex{1}\): This diffraction pattern was obtained for electrons diffracted by crystalline silicon. Bright regions are those of constructive interference, while dark regions are those of destructive interference. (credit: Ndthe, Wikimedia Commons)

Example \(\PageIndex{1}\): Electron Wavelength versus Velocity and Energy

For an electron having a de Broglie wavelength of 0.167 nm (appropriate for interacting with crystal lattice structures that are about this size): (a) Calculate the electron’s velocity, assuming it is nonrelativistic. (b) Calculate the electron’s kinetic energy in eV.

Strategy

For part (a), since the de Broglie wavelength is given, the electron’s velocity can be obtained from \(\lambda=h / p\) by using the nonrelativistic formula for momentum, \(p=m v\). For part (b), once \(v\) is obtained (and it has been verified that \(v\) is nonrelativistic), the classical kinetic energy is simply \((1 / 2) m v^{2}\).

Solution for (a)

Substituting the nonrelativistic formula for momentum (\(p=m v\)) into the de Broglie wavelength gives

\[\lambda=\frac{h}{p}=\frac{h}{m v}. \nonumber\]

Solving for \(v\) gives

\[v=\frac{h}{m \lambda}. \nonumber\]

Substituting known values yields

\[v=\frac{6.63 \times 10^{-34} \mathrm{~J} \cdot \mathrm{s}}{\left(9.11 \times 10^{-31} \mathrm{~kg}\right)\left(0.167 \times 10^{-9} \mathrm{~m}\right)}=4.36 \times 10^{6} \mathrm{~m} / \mathrm{s}. \nonumber\]

Solution for (b)

While fast compared with a car, this electron’s speed is not highly relativistic, and so we can comfortably use the classical formula to find the electron’s kinetic energy and convert it to eV as requested.

\[\begin{aligned}
\mathrm{KE} &=\frac{1}{2} m v^{2} \\
&=\frac{1}{2}\left(9.11 \times 10^{-31} \mathrm{~kg}\right)\left(4.36 \times 10^{6} \mathrm{~m} / \mathrm{s}\right)^{2} \\
&=\left(8.66 \times 10^{-18} \mathrm{~J}\right)\left(\frac{1 ~\mathrm{eV}}{1.602 \times 10^{-19} \mathrm{~J}}\right) \\
&=54.05 ~\mathrm{eV}
\end{aligned} \nonumber\]

Discussion

This low energy means that these 0.167-nm electrons could be obtained by accelerating them through a 54.0-V electrostatic potential, an easy task. The results also confirm the assumption that the electrons are nonrelativistic, since their velocity is just over 1% of the speed of light and the kinetic energy is about 0.01% of the rest energy of an electron (0.511 MeV). If the electrons had turned out to be relativistic, we would have had to use more involved calculations employing relativistic formulas.

Electron Microscopes

One consequence or use of the wave nature of matter is found in the electron microscope. As we have discussed, there is a limit to the detail observed with any probe having a wavelength. Resolution, or observable detail, is limited to about one wavelength. Since a potential of only 54 V can produce electrons with sub-nanometer wavelengths, it is easy to get electrons with much smaller wavelengths than those of visible light (hundreds of nanometers). Electron microscopes can, thus, be constructed to detect much smaller details than optical microscopes. (See Figure \(\PageIndex{2}\).)

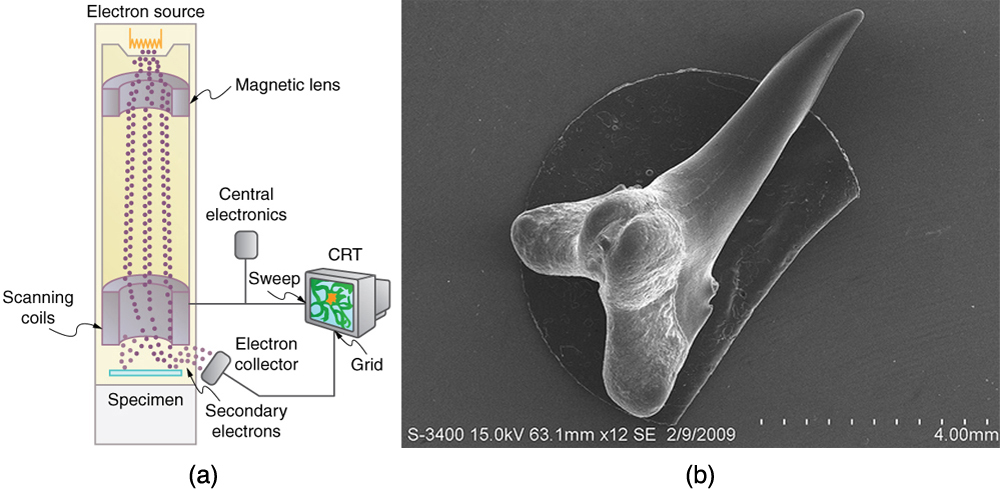
There are basically two types of electron microscopes. The transmission electron microscope (TEM) accelerates electrons that are emitted from a hot filament (the cathode). The beam is broadened and then passes through the sample. A magnetic lens focuses the beam image onto a fluorescent screen, a photographic plate, or (most probably) a CCD (light sensitive camera), from which it is transferred to a computer. The TEM is similar to the optical microscope, but it requires a thin sample examined in a vacuum. However it can resolve details as small as 0.1 nm (\(10^{-10} \mathrm{~m}\)), providing magnifications of 100 million times the size of the original object. The TEM has allowed us to see individual atoms and structure of cell nuclei.

The scanning electron microscope (SEM) provides images by using secondary electrons produced by the primary beam interacting with the surface of the sample (see Figure \(\PageIndex{1}\)). The SEM also uses magnetic lenses to focus the beam onto the sample. However, it moves the beam around electrically to “scan” the sample in the x and y directions. A CCD detector is used to process the data for each electron position, producing images like the one at the beginning of this chapter. The SEM has the advantage of not requiring a thin sample and of providing a 3-D view. However, its resolution is about ten times less than a TEM.

Figure \(\PageIndex{2}\): Schematic of a scanning electron microscope (SEM) (a) used to observe small details, such as those seen in this image of a tooth of a Himipristis, a type of shark (b). (credit: Dallas Krentzel, Flickr)

Electrons were the first particles with mass to be directly confirmed to have the wavelength proposed by de Broglie. Subsequently, protons, helium nuclei, neutrons, and many others have been observed to exhibit interference when they interact with objects having sizes similar to their de Broglie wavelength. The de Broglie wavelength for massless particles was well established in the 1920s for photons, and it has since been observed that all massless particles have a de Broglie wavelength \(\lambda=h / p\) The wave nature of all particles is a universal characteristic of nature, and the de Broglie wavelength gives insight into two additional quantum mechanical ideas we will look at: the uncertainty principle (the idea that it is fundamentally and theoretically impossible to measure momentum and position of a particle precisely) and the Bohr's model of the hydrogen atom. The de Broglie wavelength relationship is the gateway connecting the wave nature (wavelength) of all particles with their particle nature (momentum).

Section Summary

• Particles of matter also have a wavelength, called the de Broglie wavelength, given by \(\lambda=\frac{h}{p}\), where \(p\) is momentum.
• The de Broglie relationship between wavelength and momentum is universally applicable to all particles and waves.
• Matter is found to have the same interference characteristics as any other wave.

Glossary

de Broglie wavelength

the wavelength possessed by a particle of matter, calculated by \(\lambda=h / p\)