7.11: Boundary Conditions on the Magnetic Field Intensity (H)
( \newcommand{\kernel}{\mathrm{null}\,}\)
In homogeneous media, electromagnetic quantities vary smoothly and continuously. At a boundary between dissimilar media, however, it is possible for electromagnetic quantities to be discontinuous. Continuities and discontinuities in fields can be described mathematically by boundary conditions and used to constrain solutions for fields away from these boundaries. In this section, we derive boundary conditions on the magnetic field intensity H.
To begin, consider a region consisting of only two media that meet at a smooth boundary as shown in Figure 7.11.1. The desired boundary condition can be obtained directly from Ampere’s Circuital Law (ACL):
∮CH⋅dl=Iencl
where C is any closed path and Iencl is the current that flows through the surface bounded by that path in the direction specified by the “right-hand rule” of Stokes’ theorem.
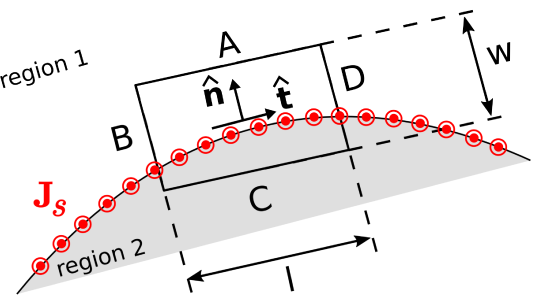 Figure 7.11.1: Determining the boundary condition on H at the smooth boundary between two material regions.
Figure 7.11.1: Determining the boundary condition on H at the smooth boundary between two material regions.
Let C take the form of a rectangle centered on a point on the boundary as shown in Figure 7.11.1, perpendicular to the direction of current flow at that location. Let the sides A, B, C, and D be perpendicular and parallel to the boundary. Let the length of the parallel sides be l, and let the length of the perpendicular sides be w. Now we apply ACL. We must integrate in a counter-clockwise direction in order to be consistent with the indicated reference direction for Js. Thus:
∮H⋅dl=∫AH⋅dl+∫BH⋅dl+∫CH⋅dl+∫DH⋅dl=Iencl
Now we let w and l become vanishingly small while (1) maintaining the ratio l/w and (2) keeping C centered on the boundary. In this process, the contributions from the B and D segments become equal in magnitude but opposite in sign; i.e.,
∫BH⋅dl+∫DH⋅dl→0
This leaves ∫AH⋅dl+∫CH⋅dl→Iencl
Let us define the unit vector ˆt (“tangent”) as shown in Figure 7.11.1. Now we have simply:
H1⋅(−ˆtΔl)+H2⋅(+ˆtΔl)=Iencl
where H1 and H2 are the fields evaluated on the two sides of the boundary, and Δl→0 is the length of sides A and C. As always, Iencl (units of A) may be interpreted as the flux of the current density Js (units of A/m) flowing past a line on the surface having length Δl (units of m) perpendicular to ˆt׈n, where ˆn is the normal to the surface, pointing into Region 1. Stated mathematically:
Iencl→Js⋅(Δl ˆt׈n)
Before proceeding, note this is true regardless of the particular direction we selected for ˆt; it is only necessary that ˆt be tangent to the boundary. Thus, ˆt׈n need not necessarily be in the same direction as Js. Now Equation ??? can be written:
H2⋅ˆtΔl−H1⋅ˆtΔl=Js⋅(ˆt׈n)Δl
Eliminating the common factor of Δl and arranging terms on the left:
(H2−H1)⋅ˆt=Js⋅(ˆt׈n)
The right side may be transformed using a vector identity (A⋅(B×C)=B⋅(C×A)=C⋅(A×B) of Section B3) to obtain:
(H2−H1)⋅ˆt=ˆt⋅(ˆn×Js)
Equation ??? is the boundary condition we seek. We have found that the component of H2−H1 (the difference between the magnetic field intensities at the boundary) in any direction tangent to the boundary is equal to the component of the current density flowing in the perpendicular direction ˆn×Js. Said differently:
A discontinuity in the tangential component of the magnetic field intensity at the boundary must be supported by surface current flowing in a direction perpendicular to this component of the field.
An important consequence is that:
If there is no surface current, then the tangential component of the magnetic field intensity is continuous across the boundary.
It is possible to obtain a mathematical form of the boundary condition that is more concise and often more useful than Equation ???. This form may be obtained as follows. First, we note that the dot product with respect to ˆt on both sides of Equation ??? means simply “any component that is tangent to the boundary.” We need merely to make sure we are comparing the same tangential component on each side of the equation. For example ˆn×(H2−H1) is tangential to the boundary, since ˆn is perpendicular to the boundary and therefore any cross product involving ˆn will be perpendicular to ˆn. The corresponding component of the current density is ˆn×(ˆn×Js), so Equation ??? may be equivalently written as follows:
ˆn×(H2−H1)=ˆn׈n×Js
Applying a vector identity (A×(B×C)=B(A⋅C)−C(A⋅B) of Section B3) to the right side of Equation ??? we obtain:
ˆn׈n×Js=ˆn(ˆn⋅Js)−Js(ˆn⋅ˆn)=ˆn(0)−Js(1)=−Js
Therefore:
ˆn×(H2−H1)=−Js
The minus sign on the right can be eliminated by swapping H2 and H1 on the left, yielding
ˆn×(H1−H2)=Js
This is the form in which the boundary condition is most commonly expressed.
It is worth noting what this means for the magnetic field intensity B. Since B=μH:
In the absence of surface current, the tangential component of B across the boundary between two material regions is discontinuous if the permeabilities are unequal.


