1.9: Gauss's Theorem
( \newcommand{\kernel}{\mathrm{null}\,}\)
A point charge Q is at the centre of a sphere of radius r. Calculate the D-flux through the sphere. Easy. The magnitude of D at a distance a is Q/(4(πr2) and the surface area of the sphere is 4πr2. Therefore the flux is just Q. Notice that this is independent of r; if you double r, the area is four times as great, but D is only a quarter of what it was, so the total flux remains the same. You will probably agree that if the charge is surrounded by a shape such as shown in Figure I.8, which is made up of portions of spheres of different radii, the D-flux through the surface is still just Q. And you can distort the surface as much as you like, or you may consider any surface to be made up of an infinite number of infinitesimal spherical caps, and you can put the charge anywhere you like inside the surface, or indeed you can put as many charges inside as you like – you haven’t changed the total normal component of the flux, which is still just Q. This is Gauss’s theorem, which is a consequence of the inverse square nature of Coulomb’s law.
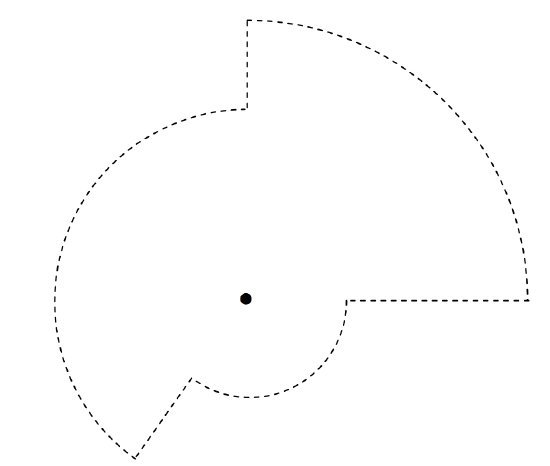
FIGURE I.8
Gauss’s theorem
The total normal component of the D-flux through any closed surface is equal to the charge enclosed by that surface.
Examples
A long rod carries a charge of λ per unit length. Construct around it a cylindrical surface of radius r and length l. The charge enclosed is lλ, and the field is directed radially outwards, passing only through the curved surface of the cylinder. The D-flux through the cylinder is lλ and the area of the curved surface is 2πrl, so D=lλ/(2πrl) and hence E=λ/(2πϵr).
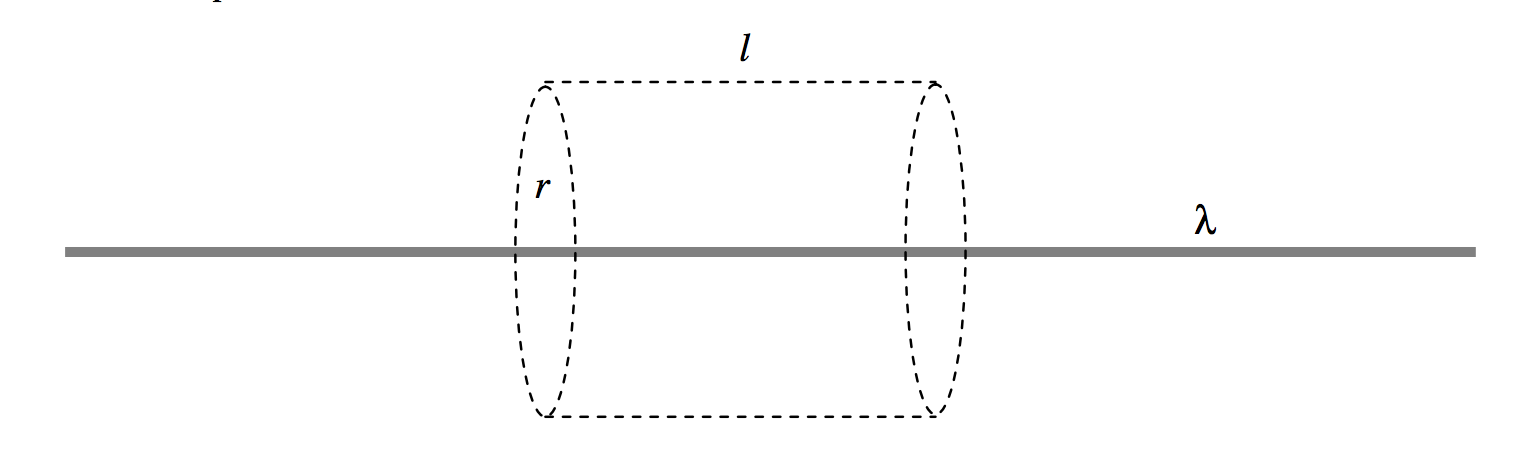
FIGURE I.9
A flat plate carries a charge of σ per unit area. Construct around it a cylindrical surface of cross-sectional area A. The charge enclosed by the cylinder is Aσ, so this is the D-flux through the cylinder. It all goes through the two ends of the cylinder, which have a total area 2A, and therefore D = σ/2 and E=σ/(2ϵ).
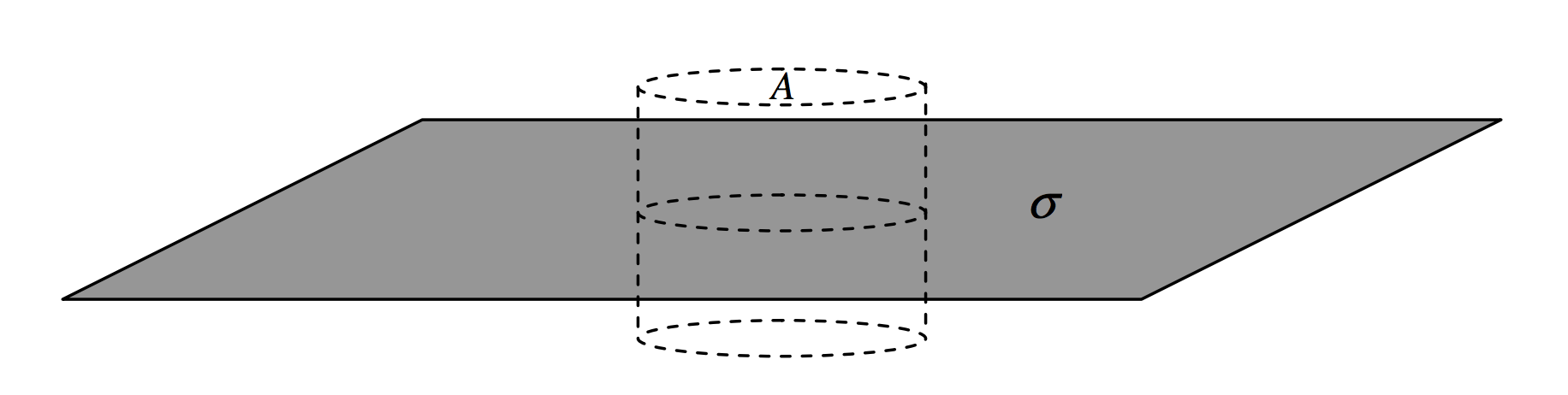
FIGURE I.10
A hollow spherical shell of radius a carries a charge Q. Construct two gaussian spherical surfaces, one of radius less than a and the other of radius r>a. The smaller of these two surfaces has no charge inside it; therefore the flux through it is zero, and so E is zero. The charge through the larger sphere is Q and is area is 4πr2. Therefore D=Q/(4πr2) and E=Q/(4πϵr2). (It is worth going to Chapter 5 of Celestial Mechanics, subsection 5.4.8, to go through the calculus derivation, so that you can appreciate Gauss’s theorem all the more.)
A point charge Q is in the middle of a cylinder of radius a and length 2l. Calculate the flux through the cylinder.
An infinite rod is charged with λ coulombs per unit length. It passes centrally through a spherical surface of radiusa. Calculate the flux through the spherical surface.
These problems are done by calculus in section 5.6 of Celestial Mechanics, and furnish good examples of how to do surface integrals, and I recommend that you work through them. However, it is obvious from Gauss’s theorem that the answers are just Q and 2aλ respectively.
A point charge Q is in the middle of a cube of side 2a. The flux through the cube is, by Gauss’s theorem, Q, and the flux through one face is Q/6. I hope you enjoyed doing this by calculus in section 1.8.


