5.2: Plane Parallel Capacitor
- Page ID
- 5439
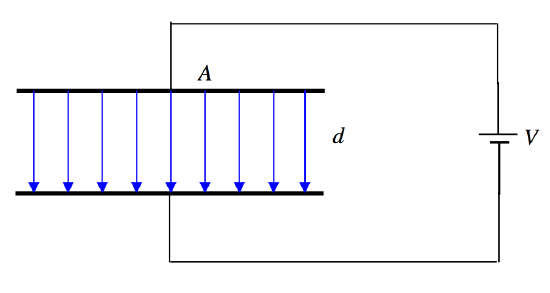
\(\text{FIGURE V.3}\)
We have a capacitor whose plates are each of area \(A\), separation \(d\), and the medium between the plates has permittivity \(\epsilon\). It is connected to a battery of EMF \(V\), so the potential difference across the plates is \(V\). The electric field between the plates is \(E = V/d\), and therefore \(D = \epsilon V/d\). The total \(D\)-flux arising from the positive plate is \(DA\), and, by Gauss’s law, this must equal \(Q\), the charge on the plate.
Thus \(Q=\epsilon AV/d\) and therefore the capacitance is
\[C=\frac{\epsilon A}{d}\label{5.2.1}\]
Verify that this is dimensionally correct, and note how the capacitance depends upon \(\epsilon\), \(A\) and \(d\).
In Section 1.5 we gave the SI units of permittivity as \(\text{C}^2\text{N}^{-1}\text{ m}^{-2}\). Equation \ref{5.2.1} shows that a more convenient SI unit for permittivity is \(\text{F m}^{-1}\), or farads per metre.
Question: If the separation of the plates is not small, so that the electric field is not uniform, and the field lines bulge outwards at the edge, will the capacitance be less than or greater than \(\epsilon A/d\)?