5.21: More on E, D, P, etc
( \newcommand{\kernel}{\mathrm{null}\,}\)
I’ll review a few things that we have already covered before going on. The electric field E between the plates of a plane parallel capacitor is equal to the potential gradient – i.e. the potential difference between the plates divided by the distance between them.
The electric field D between the plates of a plane parallel capacitor is equal to the surface charge density on the plates.
Suppose at first there is nothing between the plates. If you now thrust an isotropic* dielectric material of relative permittivity ϵr between the plates, what happens? Answer: If the plates are isolated D remains the same while E (and hence the potential difference across the plates) is reduced by a factor ϵr. If on the other hand the plates are connected to a battery, the potential difference and hence E remains the same while D (and hence the charge density on the plates) increases by a factor ϵr.
You will have noticed the word isotropic here. Refer to Section 1.7 for a brief mention of an anisotropic medium, and the concept of permittivity as a tensor quantity. I’m not concerned with this aspect here.
In either case, the block of dielectric material becomes polarized. It develops a charge density on the surfaces that adjoin the plates. The block of material develops a dipole moment, and the dipole moment divided by the volume of the material – i.e. the dipole moment per unit volume – is the polarization P of the material. P is also equal to D−ϵ0E and, of course, to ϵE−ϵ0E. The ratio of the resulting polarization P to the polarizing field ϵ0E is called the electric susceptibility χ of the medium. It will be worth spending a few moments convincing yourself from these definitions and concepts that ϵ=ϵ0(1+χ) and χ=ϵr−1, where ϵr is the dimensionless relative permittivity (or dielectric constant) ϵ/ϵ0.
What is happening physically inside the medium when it becomes polarized? One possibility is that the individual molecules, if they are asymmetric molecules, may already possess a permanent dipole moment. The molecule carbon dioxide, which, in its ground state, is linear and symmetric, O=C=O, does not have a permanent dipole moment. Symmetric molecules such as CH4, and single atoms such as He, do not have a permanent dipole moment. The water molecule has some elements of symmetry, but it is not linear, and it does have a permanent dipole moment, of about 6×10−30 C m, directed along the bisector of the HOH angle and away from the O atom. If the molecules have a permanent dipole moment and are free to rotate (as, for example, in a gas) they will tend to rotate in the direction of the applied field. (I’ll discuss that phrase “tend to” in a moment.) Thus the material becomes polarized.
A molecule such as CH4 is symmetric and has no permanent dipole moment, but, if it is placed in an external electric field, the molecule may become distorted from its perfect tetrahedral shape with neat 109º angles, because each pair of CH atoms has a dipole moment. Thus the molecule acquires an induced dipole moment, and the material as a whole becomes polarized. The ratio of the induced dipole moment p to the polarizing field E polarizability α of the molecule. Review Section 3.6 for more on this.
How about a single atom, such as Kr? Even that can acquire a dipole moment. Although there are no bonds to bend, under the influence of an electric field a preponderance of electrons will migrate to one side of the atom, and so the atom acquires a dipole moment. The same phenomenon applies, of course, to a molecule such as CH4 in addition to the bond bending already mentioned.
Let us consider the situation of a dielectric material in which the molecules have a permanent dipole moment and are free (as in a gas, for example) to rotate. We’ll suppose that, at least in a weak polarizing field, the permanent dipole moment is significantly larger than any induced dipole moment, so we’ll neglect the latter. We have said that, under the influence of a polarizing field, the permanent dipole will tend to align themselves with the field. But they also have to contend with the constant jostling and collisions between molecules, which knock their dipole moments haywire, so they can’t immediately all align exactly with the field. We might imagine that the material may become fairly strongly polarized if the temperature is fairly low, but only relatively weakly polarized at higher temperatures. Dare we even hope that we might be able to predict the variation of polarization P with temperature T? Let’s have a go!
We recall (Section 3.4) that the potential energy U of a dipole, when it makes an angle θ with the electric field, is
U=−pEcosθ=−p⋅E.
The energy of a dipole whose direction makes an angle of between θ and θ+dθ with the field will be between U and U+dU, where dU=pEsinθdθ. What happens next requires familiarity with Boltzmann’s equation for distribution of energies in a statistical mechanics. See for example my Stellar Atmospheres notes, Chapter 8, Section 8.4. The fraction of molecules having energies between U and U+dU will be, following Boltzmann’s equation,
e−U/(kT)dU∫+pE−pEe−U/(kT)dU,
(Caution: Remember that here I’m using U for potential energy, and E for electric field.)
That is, the fraction of molecules making angles of between θ and θ+dθ with the field is
pEepEcosθ/(kT)sinθdθ∫π0pEepEcosθ/(kT)sinθdθ=epEcosθ/(kT)sinθdθ∫π0epEcosθ/(kT)sinθdθ.
The component in the direction of E of the dipole moment of this fraction of the molecules is
p∫π0epEcosθ/(kT)sinθcosθdθ∫π0epEcosθ/(kT)sinθdθ,
and this expression represents the induced dipole moment in the direction of the field of the entire sample, which I’ll call ps. The polarization of the sample would be this divided by its volume.
Let
x=pEkTcosθ=acosθ.
Then the expression for the dipole moment of the entire sample becomes (some care is needed):
ps=p×∫+a−axexdxa∫+a−aexdx=p×(ea+e−aea−e−a−1a).
The expression in parentheses is called the Langevin function, and it was first derived in connection with the theory of paramagnetism. If your calculator or computer supports the hyperbolic coth function, it is most easily calculated as coth a−1/a. If it does not support coth, calculate it as
1+b1−b−1a
where b=e−2a. In any case it is a rather interesting, even challenging, function. Let us call the expression in parentheses f(a). What would the function look like it you were to plot f(a) versus a? The derivative with respect to a is
1a2−4b(1−b)2.
It is easy to see that, as a→∞, the function approaches 1 and its derivative, or slope, approaches zero. But what are the function and its derivative (slope) at a=0? You may find that a bit of a challenge. The answer is that, as a→0, the function approaches zero and its derivative approaches 1/3. (In fact, for small a, the Langevin function is approximately a3(1−a), and for very small a, it is 13a.) Thus, for small a (i.e. hot temperatures) ps approaches p×kTpE3kT and no higher. The Langevin function looks like this:
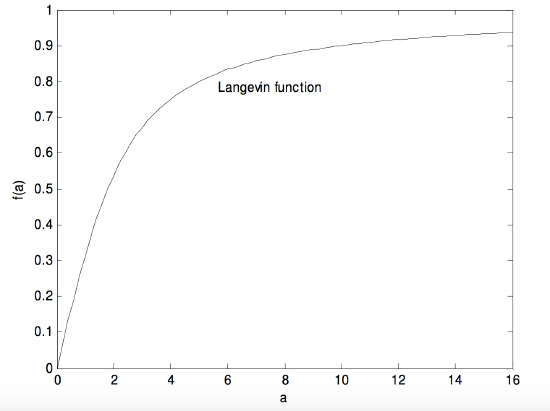
FIGURE V.28
It may be more interesting to see directly how the sample dipole moment varies with temperature. If we express the sample dipole moment ps in units of the molecular dipole moment p, and the temperature in units of pE/k, then equation 5.22.6 becomes
ps=e1/T+e−1/Te1/T−e−1/T−T=coth(1/T)−T,
and that looks like this
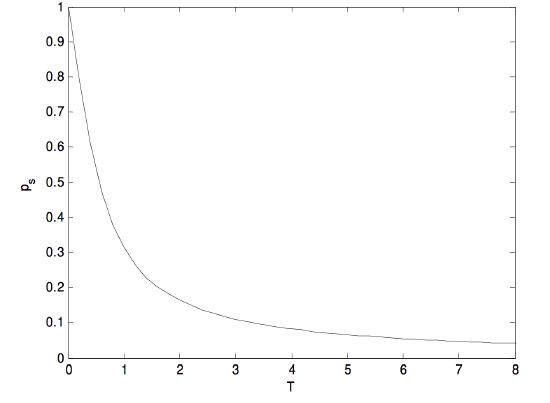
FIGURE V.29
The contribution to the polarization of a sample from the other two mechanisms – namely bond bending, and the pushing of electrons to one side, is independent of temperature. Thus, if we find that the polarization is temperature dependent, this tells us of the existence of a permanent dipole moment, as, for example, in methyl chloride CH3Cl and H2O. Indeed the temperature dependence of the polarization is part of the evidence that tells us that the water molecule is nonlinear. For small a (recall that a=pEkT), the polarization of the material is pE3kT, and so a graph of the polarization versus 1/T will be a straight line from which one can determine the dipole moment of the molecule – the greater the slope, the greater the dipole moment. On the other hand, if the polarization is temperature-independent, then the molecule is symmetric, such as methane CH4 and OCO. Indeed the independence of the polarization on temperature is part of the evidence that tells us that CO2 is a linear molecule.


