5.12: Evanescent Waves
\newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }
\newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}}
\newcommand{\id}{\mathrm{id}} \newcommand{\Span}{\mathrm{span}}
( \newcommand{\kernel}{\mathrm{null}\,}\) \newcommand{\range}{\mathrm{range}\,}
\newcommand{\RealPart}{\mathrm{Re}} \newcommand{\ImaginaryPart}{\mathrm{Im}}
\newcommand{\Argument}{\mathrm{Arg}} \newcommand{\norm}[1]{\| #1 \|}
\newcommand{\inner}[2]{\langle #1, #2 \rangle}
\newcommand{\Span}{\mathrm{span}}
\newcommand{\id}{\mathrm{id}}
\newcommand{\Span}{\mathrm{span}}
\newcommand{\kernel}{\mathrm{null}\,}
\newcommand{\range}{\mathrm{range}\,}
\newcommand{\RealPart}{\mathrm{Re}}
\newcommand{\ImaginaryPart}{\mathrm{Im}}
\newcommand{\Argument}{\mathrm{Arg}}
\newcommand{\norm}[1]{\| #1 \|}
\newcommand{\inner}[2]{\langle #1, #2 \rangle}
\newcommand{\Span}{\mathrm{span}} \newcommand{\AA}{\unicode[.8,0]{x212B}}
\newcommand{\vectorA}[1]{\vec{#1}} % arrow
\newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow
\newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }
\newcommand{\vectorC}[1]{\textbf{#1}}
\newcommand{\vectorD}[1]{\overrightarrow{#1}}
\newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}}
\newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}}
\newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }
\newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}}
\newcommand{\avec}{\mathbf a} \newcommand{\bvec}{\mathbf b} \newcommand{\cvec}{\mathbf c} \newcommand{\dvec}{\mathbf d} \newcommand{\dtil}{\widetilde{\mathbf d}} \newcommand{\evec}{\mathbf e} \newcommand{\fvec}{\mathbf f} \newcommand{\nvec}{\mathbf n} \newcommand{\pvec}{\mathbf p} \newcommand{\qvec}{\mathbf q} \newcommand{\svec}{\mathbf s} \newcommand{\tvec}{\mathbf t} \newcommand{\uvec}{\mathbf u} \newcommand{\vvec}{\mathbf v} \newcommand{\wvec}{\mathbf w} \newcommand{\xvec}{\mathbf x} \newcommand{\yvec}{\mathbf y} \newcommand{\zvec}{\mathbf z} \newcommand{\rvec}{\mathbf r} \newcommand{\mvec}{\mathbf m} \newcommand{\zerovec}{\mathbf 0} \newcommand{\onevec}{\mathbf 1} \newcommand{\real}{\mathbb R} \newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]} \newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]} \newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]} \newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]} \newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]} \newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]} \newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]} \newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]} \newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]} \newcommand{\laspan}[1]{\text{Span}\{#1\}} \newcommand{\bcal}{\cal B} \newcommand{\ccal}{\cal C} \newcommand{\scal}{\cal S} \newcommand{\wcal}{\cal W} \newcommand{\ecal}{\cal E} \newcommand{\coords}[2]{\left\{#1\right\}_{#2}} \newcommand{\gray}[1]{\color{gray}{#1}} \newcommand{\lgray}[1]{\color{lightgray}{#1}} \newcommand{\rank}{\operatorname{rank}} \newcommand{\row}{\text{Row}} \newcommand{\col}{\text{Col}} \renewcommand{\row}{\text{Row}} \newcommand{\nul}{\text{Nul}} \newcommand{\var}{\text{Var}} \newcommand{\corr}{\text{corr}} \newcommand{\len}[1]{\left|#1\right|} \newcommand{\bbar}{\overline{\bvec}} \newcommand{\bhat}{\widehat{\bvec}} \newcommand{\bperp}{\bvec^\perp} \newcommand{\xhat}{\widehat{\xvec}} \newcommand{\vhat}{\widehat{\vvec}} \newcommand{\uhat}{\widehat{\uvec}} \newcommand{\what}{\widehat{\wvec}} \newcommand{\Sighat}{\widehat{\Sigma}} \newcommand{\lt}{<} \newcommand{\gt}{>} \newcommand{\amp}{&} \definecolor{fillinmathshade}{gray}{0.9}Consider the situation shown in Figure \PageIndex{1}:
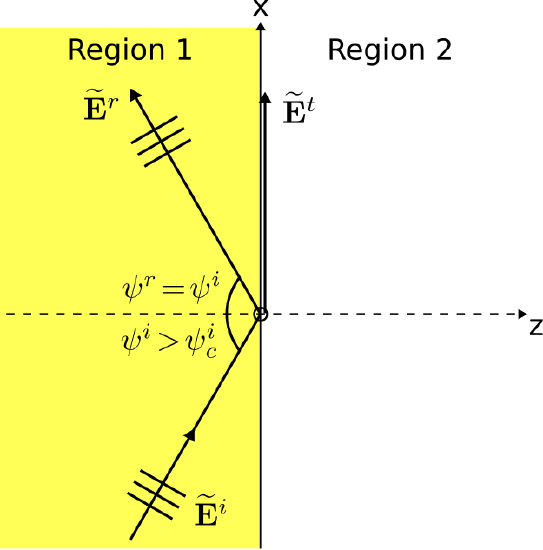 Figure \PageIndex{1}: A uniform plane wave obliquely incident on the planar boundary between two semi-infinite material regions. Here \mu_{r 1} \epsilon_{r 1}>\mu_{r 2} \epsilon_{r 2} and \psi^i > \psi^i_c. ( CC BY-SA 4.0; C. Wang)
Figure \PageIndex{1}: A uniform plane wave obliquely incident on the planar boundary between two semi-infinite material regions. Here \mu_{r 1} \epsilon_{r 1}>\mu_{r 2} \epsilon_{r 2} and \psi^i > \psi^i_c. ( CC BY-SA 4.0; C. Wang)
A uniform plane wave obliquely incident on the planar boundary between two semi-infinite material regions, and total internal reflection occurs because the angle of incidence \psi^i is greater than the critical angle
\psi^i_c = \arcsin\sqrt{\frac{\mu_{r2}\epsilon_{r2}}{\mu_{r1}\epsilon_{r1}}} \label{m0170_eCA}
Therefore, the reflection coefficient is complex-valued with magnitude equal to 1 and phase that depends on polarization and the constitutive parameters of the media.
The total reflection of the incident wave seems to contradict the boundary conditions that require the tangential components of the electric and magnetic fields to be continuous across the boundary. How can these components of the fields be continuous across the boundary if no power is transmitted across the boundary? There must be a field on the opposite side of the boundary, but – somehow – it must have zero power. To make sense of this, let us attempt to find a solution for the transmitted field.
We begin by postulating a complex-valued angle of transmission \psi^{tc}. Although the concept of a complex-valued angle may seem counterintuitive, there is mathematical support for this concept. For example, consider the well-known trigonometric identities:
\begin{align} \sin\theta &= \frac{1}{j2}\left( e^{j\theta} - e^{-j\theta} \right) \label{m0170_eSI} \\ \cos\theta &= \frac{1}{2}\left( e^{j\theta} + e^{-j\theta} \right) \label{m0170_eSC}\end{align}
These identities allow us to compute values for sine and cosine even when \theta is complex-valued. One may conclude that the sine and cosine of a complex-valued angle exist, although the results may also be complex-valued.
Based on the evidence established so far, we presume that \psi^{tc} behaves as follows:
\begin{align} \psi^{tc} &\triangleq \psi^t~\mbox{,} ~~~ ~~~ ~~~\psi^i<\psi^i_c \label{m0170_eptc1} \\ \psi^{tc} &\triangleq \pi/2~\mbox{,} ~~~ ~~~ \psi^i=\psi^i_c \label{m0170_eptc2} \\ \psi^{tc} &\triangleq \pi/2+j\psi''~\mbox{,} ~~~ \psi^i>\psi^i_c \label{m0170_eptc3}\end{align}
In other words, \psi^{tc} is identical to \psi^t for \psi^i\le\psi^i_c, but when total internal reflection occurs, we presume the real part of \psi^{tc} remains fixed (parallel to the boundary) and that an imaginary component j\psi'' emerges to satisfy the boundary conditions.
For clarity, let us assign the variable \psi' to represent the real part of \psi^{tc} in Equations \ref{m0170_eptc1}-\ref{m0170_eptc3}. Then we may refer to all three cases using a single expression as follows:
\psi^{tc} = \psi' + j\psi'' \nonumber
Now we use a well-known trigonometric identity as follows:
\begin{align} \sin{\psi^{tc}} &= \sin{\left(\psi' + j\psi''\right)} \\ &= \sin{\psi'}\cos{j\psi''} + \cos{\psi'}\sin{j\psi''} \label{m0170_eSptc}\end{align}
Using Equation \ref{m0170_eSC}, we find:
\begin{aligned} \cos{j\psi''} &= \frac{1}{2}\left( e^{j\left(j\psi''\right)} + e^{-j\left(j\psi''\right)} \right) \\ &= \frac{1}{2}\left( e^{-\psi''} + e^{+\psi''} \right) \\ &= \cosh{\psi''}\end{aligned} \nonumber
In other words, the cosine of j\psi'' is simply the hyperbolic cosine (“\cosh”) of \psi''. Interestingly, \cosh of a real-valued argument is real-valued, so \cos{j\psi''} is real-valued.
Using Equation \ref{m0170_eSI}, we find:
\begin{align} \sin{j\psi''} &= \frac{1}{j2}\left( e^{j\left(j\psi''\right)} - e^{-j\left(j\psi''\right)} \right) \\ &= \frac{1}{j2}\left( e^{-\psi''} - e^{+\psi''} \right) \\ &= j\frac{1}{2}\left( e^{+\psi''} - e^{-\psi''} \right) \\ &= j\sinh{\psi''}\end{align} \nonumber
In other words, the sine of j\psi'' is j times hyperbolic sine (“\sinh”) of \psi''. Now note that \sinh of a real-valued argument is real-valued, so \sin{j\psi''} is imaginary-valued.
Using these results, we find Equation \ref{m0170_eSptc} may be written as follows:
\sin{\psi^{tc}} = \sin{\psi'}\cosh{\psi''} + j\cos{\psi'}\sinh{\psi''} \label{m0170_eStc2}
Using precisely the same approach, we find:
\cos{\psi^{tc}} = \cos{\psi'}\cosh{\psi''} - j\sin{\psi'}\sinh{\psi''} \label{m0170_eCtc2}
Before proceeding, let’s make sure Equations \ref{m0170_eStc2} and \ref{m0170_eCtc2} exhibit the expected behavior before the onset of total internal reflection. For \psi^i<\psi^i_c, \psi'=\psi^t and \psi''=0. In this case, \sinh\psi''=0, \cosh\psi''=1, and Equations \ref{m0170_eStc2} and \ref{m0170_eCtc2} yield
\begin{aligned} \sin{\psi^{tc}} &= \sin{\psi^t} \\ \cos{\psi^{tc}} &= \cos{\psi^t}\end{aligned} \nonumber
as expected.
When total internal reflection is in effect, \psi^i>\psi^i_c, so \psi'=\pi/2. In this case, Equations \ref{m0170_eStc2} and \ref{m0170_eCtc2} yield
\begin{align} \sin{\psi^{tc}} &= \cosh{\psi''} \\ \cos{\psi^{tc}} &= -j\sinh{\psi''}\end{align} \nonumber
Let us now consider what this means for the field in Region 2. According to the formalism adopted in previous sections, the propagation of wave components in this region is described by the factor e^{-j{\bf k}^t\cdot{\bf r}} where
\begin{align} {\bf k}^t &= \beta_2\hat{\bf k}^t \nonumber \\ &= \beta_2\left( \hat{\bf x}\sin\psi^{tc} + \hat{\bf z}\cos\psi^{tc} \right) \end{align} \nonumber
and
{\bf r} = \hat{\bf x}x + \hat{\bf y}y + \hat{\bf z}z \nonumber
so
\begin{align} {\bf k}^t\cdot{\bf r} &= \left(\beta_2\sin\psi^{tc}\right)x + \left(\beta_2\cos\psi^{tc}\right)z \nonumber \\ &= \left(\beta_2\cosh{\psi''}\right)x + \left(-j\beta_2\sinh{\psi''}\right)z \end{align} \nonumber
Therefore, the wave in Region 2 propagates according to
\begin{aligned} e^{-j{\bf k}^t\cdot{\bf r}} &= e^{-j\left(\beta_2\cosh{\psi''}\right)x}e^{-\left(\beta_2\sinh{\psi''}\right)z} \label{m0170_eEv1}\end{aligned}
Note that the constants \beta_2\cosh{\psi''} and \beta_2\sinh{\psi''} are both real-valued and positive. Therefore, Equation \ref{m0170_eEv1} describes a wave which propagates in the +\hat{\bf x} direction, but which is not uniform. Specifically, the magnitude of the transmitted field decreases exponentially with increasing z; i.e., maximum at the boundary, asymptotically approaching zero with increasing distance from the boundary. This wave is unlike the incident or reflected waves (both uniform plane waves), and is unlike the transmitted wave in the \psi^i<\psi^i_c case (also a uniform plane wave). The transmitted wave that we have derived in the \psi^i>\psi^i_c case gives the impression of being somehow attached to the boundary, and so may be described as a surface wave. However, in this case we have a particular kind of surface wave, known as an evanescent wave. Summarizing:
When total internal reflection occurs, the transmitted field is an evanescent wave; i.e., a surface wave which conveys no power and whose magnitude decays exponentially with increasing distance into Region 2.
At this point, we could enforce the “phase matching” condition at the boundary, which would lead us to a new version of Snell’s law that would allow us to solve for \psi'' in terms of \psi^i and the constitutive properties of the media comprising Regions 1 and 2. We could subsequently determine values for the phase propagation and attenuation constants for the evanescent wave. It suffices to say that the magnitude of the evanescent field becomes negligible beyond a few wavelengths of the boundary.
Finally, we return to the strangest characteristic of this field: It acts like a wave, but conveys no power. This field exists solely to enforce the electromagnetic boundary conditions at the boundary, and does not exist independently of the incident and reflected field. The following thought experiment may provide some additional insight.
In this experiment, a laser illuminates a planar boundary between two material regions, with conditions such that total internal reflection occurs. Thus, all incident power is reflected, and an evanescent wave exists on the opposite side of the boundary. Next, the laser is turned off. All the light incident on the boundary reflects from the boundary and continues to propagate to infinity, even after light is no longer incident on the boundary. In contrast, the evanescent wave vanishes at the moment laser light ceases to illuminate the boundary. In other words, the evanescent field does not continue to propagate along the boundary to infinity. The reason for this is simply that there is no power – hence, no energy – in the evanescent wave.


