10.9: Equivalent Circuit Model for Reception
( \newcommand{\kernel}{\mathrm{null}\,}\)
In this section, we begin to address antennas as devices that convert incident electromagnetic waves into potentials and currents in a circuit. It is convenient to represent this process in the form of a Thévenin equivalent circuit. The particular circuit addressed in this section is shown in Figure 10.9.1.
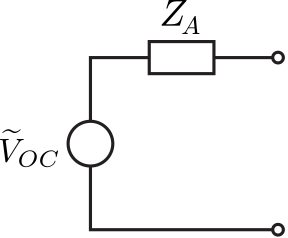 Figure 10.9.1: Thévenin equivalent circuit for an antenna in the presence of an incident electromagnetic wave. (CC BY-SA 4.0 (modified); S. Lally)
Figure 10.9.1: Thévenin equivalent circuit for an antenna in the presence of an incident electromagnetic wave. (CC BY-SA 4.0 (modified); S. Lally)
The circuit consists of a voltage source ˜VOC and a series impedance ZA. The source potential ˜VOC is the potential at the terminals of the antenna when there is no termination; i.e., when the antenna is open-circuited. The series impedance ZA is the output impedance of the circuit, and so determines the magnitude and phase of the current at the terminals once a load is connected. Given ˜VOC and the current through the equivalent circuit, it is possible to determine the power delivered to the load. Thus, this model is quite useful, but only if we are able to determine ˜VOC and ZA. This section provides an informal derivation of these quantities that is sufficient to productively address the subsequent important topics of effective aperture and impedance matching of receive antennas.1
Vector effective length
With no derivation required, we can deduce the following about ˜VOC:
- ˜VOC must depend on the incident electric field intensity ˜Ei. Presumably the relationship is linear, so ˜VOC is proportional to the magnitude of ˜Ei.
- Since ˜Ei is a vector whereas ˜VOC is a scalar, there must be some vector le for which
˜VOC=˜Ei⋅le
- Since ˜Ei has SI base units of V/m and ˜VOC has SI base units of V, le must have SI base units of m; i.e., length.
- We expect that ˜VOC increases as the size of the antenna increases, so the magnitude of le likely increases with the size of the antenna.
- The direction of le must be related to the orientation of the incident electric field relative to that of the antenna, since this is clearly important yet we have not already accounted for this.
It may seem at this point that le is unambiguously determined, and we need merely to derive its value. However, this is not the case. There are in fact multiple unique definitions of le that will reduce the vector ˜Ei to the observed scalar ˜VOC via Equation ???. In this section, we shall employ the most commonly-used definition, in which le is referred to as vector effective length. Following this definition, the scalar part le of le=ˆlle is commonly referred to as any of the following: effective length (the term used in this book), effective height, or antenna factor.
In this section, we shall merely define vector effective length, and defer a formal derivation to Section 10.11. In this definition, we arbitrarily set ˆl, the real-valued unit vector indicating the direction of le, equal to the direction in which the electric field transmitted from this antenna would be polarized in the far field. For example, consider a ˆz-oriented electrically-short dipole (ESD) located at the origin. The electric field transmitted from this antenna would have only a ˆθ component, and no ˆϕ component (and certainly no ˆr component). Thus, ˆl=ˆθ in this case.
Applying this definition, ˜Ei⋅ˆl yields the scalar component of ˜Ei that is co-polarized with electric field radiated by the antenna when transmitting. Now le is uniquely defined to be the factor that converts this component into ˜VOC. Summarizing:
The vector effective length le=ˆlle is defined as follows: ˆl is the real-valued unit vector corresponding to the polarization of the electric field that would be transmitted from the antenna in the far field. Subsequently, the effective length le is
le≜˜VOC˜Ei⋅ˆl
where ˜VOC is the open-circuit potential induced at the antenna terminals in response to the incident electric field intensity ˜Ei.
While this definition yields an unambiguous value for le, it is not yet clear what that value is. For most antennas, effective length is quite difficult to determine directly, and one must instead determine effective length indirectly from the transmit characteristics via reciprocity. This approach is relatively easy (although still quite a bit of effort) for thin dipoles, and is presented in Section 10.11.
To provide an example of how effective length works right away, consider the ˆz-oriented ESD described earlier in this section. Let the length of this ESD be L. Let ˜Ei be a ˆθ-polarized plane wave arriving at the ESD. The ESD is open-circuited, so the potential induced in its terminals is ˜VOC. One observes the following:
- When ˜Ei arrives from anywhere in the θ=π/2 plane (i.e., broadside to the ESD), ˜Ei points in the −ˆz direction, and we find that le≈L/2. It should not be surprising that le is proportional to L; this expectation was noted earlier in this section.
- When ˜Ei arrives from the directions θ=0 or θ=π – i.e., along the axis of the ESD – ˜Ei is perpendicular to the axis of the ESD. In this case, we find that le equals zero.
Taken together, these findings suggest that le should contain a factor of sinθ. We conclude that the vector effective length for a ˆz-directed ESD of length L is
le≈ˆθL2sinθ (ESD)
A thin straight dipole of length 10 cm is located at the origin and aligned with the z-axis. A plane wave is incident on the dipole from the direction (θ=π/4,ϕ=π/2). The frequency of the wave is 30 MHz. The magnitude of the incident electric field is 10 μV/m (rms). What is the magnitude of the induced open-circuit potential when the electric field is (a) ˆθ-polarized and (b) ˆϕ-polarized?
Solution
The wavelength in this example is c/f≅10 m, so this dipole is electrically-short. Using Equation ???:
le≈ˆθ10 cm2sinπ4≈ˆθ(3.54 cm)
Thus, the effective length le=3.54 cm. When the electric field is ˆθ-polarized, the magnitude of the induced open-circuit voltage is
|˜VOC|=|˜Ei⋅le|≈(10 μV/m)ˆθ⋅ˆθ(3.54 cm)≈354 nV rms_ (a)
When the electric field is ˆϕ-polarized:
|˜VOC|≈(10 μV/m)ˆϕ⋅ˆθ(3.54 cm)≈0_ (b)
This is because the polarization of the incident electric field is orthogonal to that of the ESD. In fact, the answer to part (b) is zero for any angle of incidence (θ,ϕ).
Output impedance
The output impedance ZA is somewhat more difficult to determine without a formal derivation, which is presented in Section 10.12. For the purposes of this section, it suffices to jump directly to the result:
The output impedance ZA of the equivalent circuit for an antenna in the receive case is equal to the input impedance of the same antenna in the transmit case.
This remarkable fact is a consequence of the reciprocity property of antenna systems, and greatly simplifies the analysis of receive antennas.
Now a demonstration of how the antenna equivalent circuit can be used to determine the power delivered by an antenna to an attached electrical circuit:
Continuing with part (a) of Example 10.9.1: If this antenna is terminated into a conjugate-matched load, then what is the power delivered to that load? Assume the antenna is lossless.
Solution
First, we determine the impedance ZA of the equivalent circuit of the antenna. This is equal to the input impedance of the antenna in transmission. Let RA and XA be the real and imaginary parts of this impedance; i.e., ZA=RA+jXA. Further, RA is the sum of the radiation resistance Rrad and the loss resistance. The loss resistance is zero because the antenna is lossless. Since this is an ESD:
Rrad≈20π2(Lλ)2
Therefore, RA=Rrad≈4.93 mΩ. We do not need to calculate XA, as will become apparent in the next step.
A conjugate-matched load has impedance Z∗A, so the potential ˜VL across the load is
˜VL=˜VOCZ∗AZA+Z∗A=˜VOCZ∗A2RA
The current ˜IL through the load is
˜IL=˜VOCZA+Z∗A=˜VOC2RA
Taking ˜VOC as an RMS quantity, the power PL delivered to the load is
PL=Re{VLI∗L}=|˜VOC|24RA
In part (a) of Example 10.9.1, |˜VOC| is found to be ≈354 nV rms, so PL≈6.33 pW_.
- Formal derivations of these quantities are provided in subsequent sections. The starting point is the section on reciprocity.↩


