8.6: Transformers as Two-Port Devices
( \newcommand{\kernel}{\mathrm{null}\,}\)
Section 8.5 explains the principle of operation of the ideal transformer. The relationship governing the terminal voltages V_1 and V_2 was found to be \frac{V_1}{V_2} = p\frac{N_1}{N_2} \nonumber where N_1 and N_2 are the number of turns in the associated coils and p is either +1 or -1 depending on the relative orientation of the windings; i.e., whether the reference direction of the associated fluxes is the same or opposite, respectively.
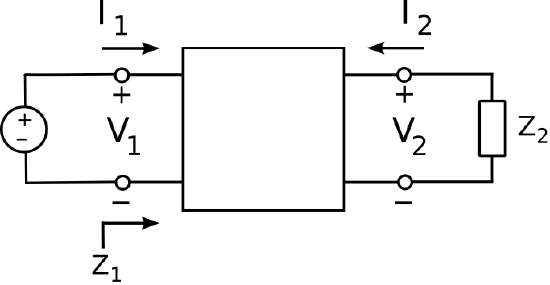 Figure \PageIndex{1}: The transformer as a two-port circuit device.
Figure \PageIndex{1}: The transformer as a two-port circuit device.
We shall now consider ratios of current and impedance in ideal transformers, using the two-port model shown in Figure \PageIndex{1}. By virtue of the reference current directions and polarities chosen in this figure, the power delivered by the source V_1 is V_1 I_1, and the power absorbed by the load Z_2 is -V_2 I_2. Assuming the transformer windings have no resistance, and assuming the magnetic flux is perfectly contained within the core, the power absorbed by the load must equal the power provided by the source; i.e., V_1 I_1 = -V_2 I_2. Thus, we have1
\boxed{ \frac{I_1}{I_2} = -\frac{V_2}{V_1} = -p\frac{N_2}{N_1} } \nonumber
We can develop an impedance relationship for ideal transformers as follows. Let Z_1 be the input impedance of the transformer; that is, the impedance looking into port 1 from the source. Thus, we have
\begin{aligned} Z_{1} & \triangleq \frac{V_{1}}{I_{1}} \\ &=\frac{+p\left(N_{1} / N_{2}\right) V_{2}}{-p\left(N_{2} / N_{1}\right) I_{2}} \\ &=-\left(\frac{N_{1}}{N_{2}}\right)^{2}\left(\frac{V_{2}}{I_{2}}\right) \end{aligned}
In Figure \PageIndex{1}, Z_2 is the the output impedance of port 2; that is, the impedance looking out port 2 into the load. Therefore, Z_2 = -V_2/I_2 (once again the minus sign is a result of our choice of sign conventions in Figure \PageIndex{1}). Substitution of this result into the above equation yields
Z_1 = \left(\frac{N_1}{N_2}\right)^2 Z_2 \nonumber
and therefore \boxed{ \frac{Z_1}{Z_2} = \left(\frac{N_1}{N_2}\right)^2 } \nonumber Thus, we have demonstrated that a transformer scales impedance in proportion to the square of the turns ratio N_1/N_2. Remarkably, the impedance transformation depends only on the turns ratio, and is independent of the relative direction of the windings (p).
The relationships developed above should be viewed as AC expressions, and are not normally valid at DC. This is because transformers exhibit a fundamental limitation in their low-frequency performance. To see this, first recall Faraday’s Law:
V = - N \frac{\partial}{\partial t} \Phi \nonumber
If the magnetic flux \Phi is not time-varying, then there is no induced electric potential, and subsequently no linking of the signals associated with the coils. At very low but non-zero frequencies, we encounter another problem that gets in the way – magnetic saturation. To see this, note we can obtain an expression for \Phi from Faraday’s Law by integrating with respect to time, yielding
\Phi(t) = -\frac{1}{N}\int_{t_0}^{t}V(\tau)d\tau + \Phi(t_0) \nonumber
where t_0 is some earlier time at which we know the value of \Phi(t_0). Let us assume that V(t) is sinusoidally-varying. Then the peak value of \Phi after t=t_0 depends on the frequency of V(t). If the frequency of V(t) is very low, then \Phi can become very large. Since the associated cross-sectional areas of the coils are presumably constant, this means that the magnetic field becomes very large. The problem with that is that most practical high-permeability materials suitable for use as transformer cores exhibit magnetic saturation; that is, the rate at which the magnetic field is able to increase decreases with increasing magnetic field magnitude (see Section 7.16). The result of all this is that a transformer may work fine at (say) 1 MHz, but at (say) 1 Hz the transformer may exhibit an apparent loss associated with this saturation. Thus, practical transformers exhibit highpass frequency response.
It should be noted that the highpass behavior of practical transistors can be useful. For example, a transformer can be used to isolate an undesired DC offset and/or low-frequency noise in the circuit attached to one coil from the circuit attached to the other coil.
The DC-isolating behavior of a transformer also allows the transformer to be used as a balun, as illustrated in Figure \PageIndex{2}. A balun is a two-port device that transforms a single-ended (“unbalanced”) signal – that is, one having an explicit connection to a datum (e.g., ground) – into a differential (“balanced”) signal, for which there is no explicit connection to a datum. Differential signals have many benefits in circuit design, whereas inputs and outputs to devices must often be in single-ended form. Thus, a common use of transformers is to effect the conversion between single-ended and differential circuits. Although a transformer is certainly not the only device that can be used as a balun, it has one very big advantage, namely bandwidth.
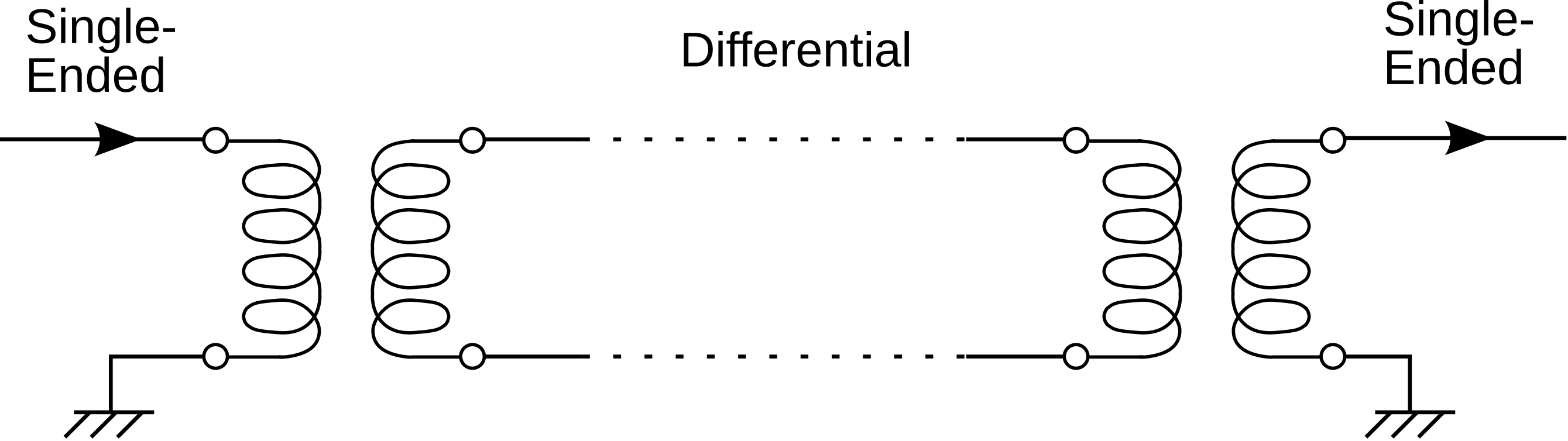 Figure \PageIndex{2}: Transformers used to convert a singleended (“unbalanced”) signal to a differential (balanced) signal, and back. (© CC BY SA 3.0 (modified); SpinningSpark)
Figure \PageIndex{2}: Transformers used to convert a singleended (“unbalanced”) signal to a differential (balanced) signal, and back. (© CC BY SA 3.0 (modified); SpinningSpark)
Additional Reading:
- S.W. Ellingson, “Differential Circuits” (Sec. 8.7) in Radio Systems Engineering, Cambridge Univ. Press, 2016.
- The minus signs in this equation are a result of the reference polarity and directions indicated in Figure \PageIndex{1}. These are more-or-less standard in electrical two-port theory (see “Additional Reading” at the end of this section), but are certainly not the only reasonable choice. If you see these expressions without the minus signs, it probably means that a different combination of reference directions/polarities is in effect.↩


