6.2: Lorentz Invariance and Bilateral Multiplication

For Hermitian matrices: $K^{\dagger}=K, \bar{K}=\tilde{K}$ and the same for R. Why bilateral multiplication? To eliminate nonphysical factors indicated as

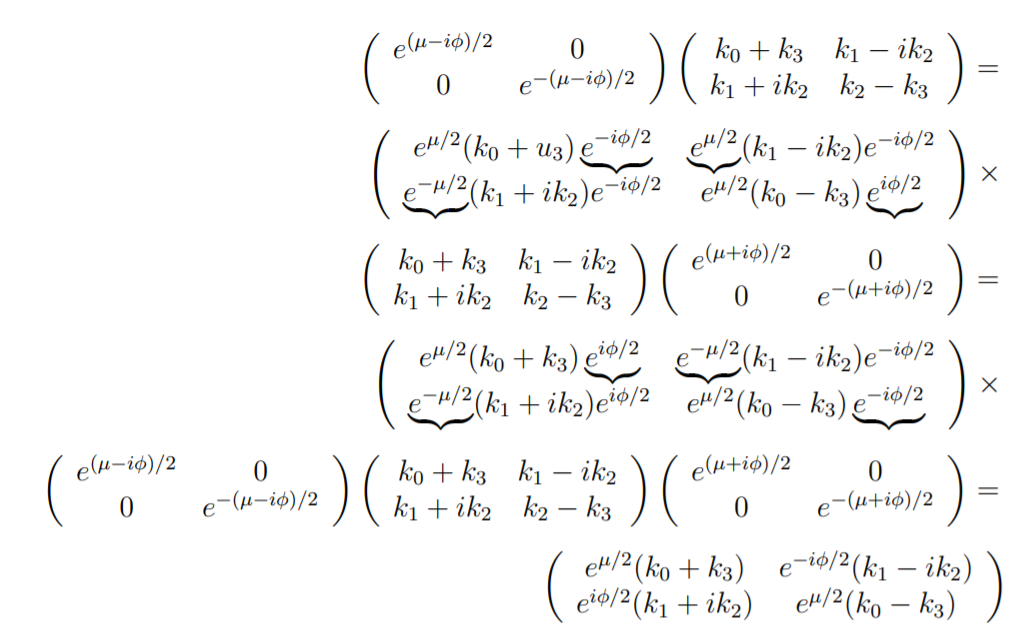
Or, in $4 \times 4$ matrix form:

$$\left(\begin{array}{c} k_{1}^{\prime} \\ k_{2}^{\prime} \\ k_{3}^{\prime} \\ k_{0}^{\prime} \end{array}\right)=\left(\begin{array}{cccc} \cos \phi & -\sin \phi & 0 & 0 \\ \sin \phi & \cos \phi & 0 & 0 \\ 0 & 0 & \cosh \mu & \sinh \mu \\ 0 & 0 & \sinh \mu & \cosh \mu \end{array}\right)\left(\begin{array}{l} k_{1} \\ k_{2} \\ k_{3} \\ k_{0} \end{array}\right)\label{1}$$

Circular rotation around the z-axis by $\phi$ and hyperbolic rotation along the same asix by th ehyperbolic angle $\mu$: Lorentz four-screw: $\mathcal{L}(\phi, \hat{z}, \mu)$. These transformations form an Abelian group.

In the Pauli algebra the formal simplicity of these relations is maintained even for arbitrary axial directions. To be sure, obtaining explicit results from the bilateral products may become cumbersome. However, the standard vectorial results can be easily extracted.