4.4: The Complex Plane

Last updated
Save as PDF

Page ID: 34536

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

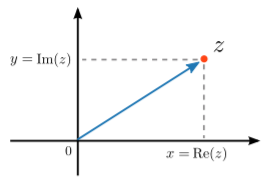
A convenient way to conceptualize a complex number is to think of it as a point on a two-dimensional plane, called the complex plane, as shown in the figure below. The real and imaginary parts are the horizontal and vertical Cartesian coordinates in the plane. The horizontal (\(x\)) and vertical (\(y\)) coordinate axes are called the “real axis” and the “imaginary axis”, respectively.

Polar representation

If we think of a complex number as a point on the complex plane, its position can also be represented using polar coordinates instead of Cartesian coordinates. For a complex number \(z = x + i y\), we can introduce polar coordinates \(r\) and \(\theta\) (both real numbers), such that \[r = \sqrt{x^2 + y^2}, \;\;\; \theta = \tan^{-1}(y/x).\] Conversely, \[x = r\cos\theta, \;\;\; y = r\sin\theta.\] These are the usual formulas for performing a change of coordinate between two-dimensional Cartesian coordinates and polar coordinates, as shown below. The radial coordinate is the magnitude of the complex number: \(r = |z|\). The azimuthal coordinate \(\theta\) is called the argument of the complex number, which is also denoted by \(\mathrm{arg}(z)\).

Note, by the way, that the complex zero, \(z = 0\), has zero magnitude and undefined argument.

Using Euler’s formula (4.3.1), we can write \[\begin{align} z &= r\cos(\theta) + i r\sin(\theta)\\ &= r \left[\cos(\theta) + i \sin(\theta)\right] \\ &= r \, e^{i\theta}.\end{align}\] Therefore, whenever we can manipulate a complex number into a form \(A e^{iB}\), where \(A\) and \(B\) are real numbers, then \(A\) is the magnitude and \(B\) is the argument. This is used in the following example:

Example \(\PageIndex{1}\)

For \(z \in \mathbb{C}\), it can be shown that the magnitude and argument of \(\exp(z)\) are: \[\left|\exp(z)\right| = e^{\mathrm{Re}(z)}, \quad \mathrm{arg}\left[\exp(z)\right] = \mathrm{Im}(z).\] Proof: Let \(z = x + i y\), where \(x, y \in \mathbb{R}\); then \[e^{z} = e^{x + i y} = e^x \, e^{iy}.\] By inspection, the magnitude of this complex number is \(e^x\), and its argument is \(y\).

Geometrical interpretation of complex operations

Using the complex plane, we can give useful geometric interpretations to the basic operations on complex numbers:

Addition of two complex numbers can be interpreted as the addition of two coordinate vectors. If \(z_1 = x_1 + i y_1\) and \(z_2 = x_2 + i y_2\), then \[z_1 + z_2 = \left(x_1 + x_2\right) + i\left(y_1 + y_2\right).\] Hence, the point corresponding to \(z_1 + z_2\) is obtained by adding the two coordinate vectors corresponding to \(z_1\) and \(z_2\). From this, we can geometrically prove a useful inequality relation between complex numbers, called the “triangle inequality”: \[|z_1 + z_2| \le |z_1| + |z_2|.\]
Complex multiplication can be interpreted as a scaling together with a rotation. If \(z_1 = r_1e^{i\theta_1}\) and \(z_2 = r_2e^{i\theta_2}\), then \[z_1 z_2 = \left(r_1 r_2\right) \,\exp[i(\theta_1 + \theta_2)].\] Hence, the point corresponding to \(z_1 \, z_2\) is obtained by scaling the \(z_1\) coordinate vector by a factor of \(|z_2|\), and rotating it by an angle of \(\theta_2\) around the origin. In particular, multiplication by \(e^{i\theta}\) is equivalent to a rotation by angle \(\theta\).
The conjugation operation (Section 4.2) is equivalent to reflection about the real axis. It moves a point from the upper half of the complex plane to the lower half, or vice versa.

Complex numbers have no ordering

One consequence of the fact that complex numbers reside in a two-dimensional plane is that inequality relations are undefined for complex numbers. This is one important difference between complex and real numbers.

Real numbers can be ordered, meaning that for any two real numbers \(a\) and \(b\), one and only one of the following is true: \[a < b \;\; \mathrm{OR} \;\; a = b \;\; \mathrm{OR}\;\; a > b.\] In geometrical terms, these ordering relations exist because the real numbers reside along a one-dimensional line.

But since complex numbers lie in a two-dimensional plane, it is nonsensical to write something like \(z_1 < z_2\), where \(z_1\) and \(z_2\) are complex numbers. (It is, however, valid to write \(|z_1| < |z_2|\), since magnitudes are real.)