5.1: The Damped Harmonic Oscillator

Last updated
Save as PDF

Page ID: 34542

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

Consider a particle of mass \(m\) subject to a spring force and a damping force. The particle can move along one dimension, with \(x(t)\) denoting its displacement at time \(t\). The damping coefficient is \(2m \gamma\), and the spring constant is \(k = m\omega_0^2\). The parameters \(m\), \(\gamma\), and \(\omega_0\) are all positive real numbers.

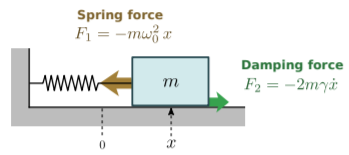
The motion of the particle can be derived using Newton’s second law: \[m \frac{d^2 x}{dt^2} = F(x,t) = - 2m\gamma \frac{dx}{dt} - m\omega_0^2 x(t).\] Dividing by the common factor of \(m\), and bringing everything to one side, gives \[\frac{d^2 x}{dt^2} + 2\gamma \frac{dx}{dt} + \omega_0^2 x(t) = 0.\] This is called the damped harmonic oscillator equation.

Note

Sometimes, we write the damped harmonic oscillator equation as: \[\left[\frac{d^2}{dt^2} + 2\gamma \frac{d}{dt} + \omega_0^2 \right]\, x(t) = 0.\] The quantity in square brackets is a linear differential operator acting on \(x(t)\). The three terms in the operator correspond to the three “ingredients” of the damped harmonic oscillator model: (i) a second derivative term stemming from Newton’s second law, (ii) a first derivative term representing the effects of damping, and (iii) a constant term representing the oscillation induced by the spring force.

Writing the equation this way helps emphasize that it is linear: i.e., any superposition of solutions is likewise a solution (see Section 5.2).

Behavior of the solution

The damped harmonic oscillator equation is a second-order ordinary differential equation (ODE). Its general solution must contain two free parameters, which are usually (but not necessarily) specified by the initial displacement \(x(0)\) and initial velocity \(\dot{x}(0)\).

For \(\gamma = 0\) (zero damping), the system reduces to the simple harmonic oscillator. From previous physics courses, we know that the general solution to the simple harmonic oscillator has the form \[x(t) = A \cos(\omega_0 t + \phi), \label{simple-gensol}\] where \(A\) and \(\phi\) are free parameters. This describes a sinusoidal motion with constant amplitude \(A\), phase \(\phi\), and frequency \(\omega_0\).

By the way, some authors call \(\omega_0\) an “angular frequency”, reserving the term “frequency” for the quantity \(f_0 = \omega_0/2\pi\). But we will always deal with \(\omega_0\) rather than \(f_0\). As such, we can refer to \(\omega_0\) as “frequency” for brevity, without risk of ambiguity.

The quantity \(\omega_0\) is directly related to the spring constant by \(k = m\omega_0^2\); in fact, this is precisely why we parameterized the spring constant in this way. It is called the natural frequency — i.e., the natural oscillation frequency of the system when damping is absent.

Eq. \(\eqref{simple-gensol}\) can be re-expressed in terms of the initial displacement \(x(0) = x_0\) and initial velocity \(\dot{x}(0) = v_0\). It is straightforward to show that \[A = \sqrt{x_0^2 + \left(\frac{v_0}{\omega_0}\right)^2}, \quad \phi = -\tan^{-1}\left(\frac{v_0}{\omega_0 x_0}\right).\]

Now consider \(\gamma > 0\). A damping force now opposes the motion, doing work against the particle and causing it to lose energy over time. Hence, the particle can no longer oscillate forever around the equilibrium position. If the damping force is relatively weak, the energy lost per cycle is relatively small, so the motion of the particle should consist of an oscillation whose amplitude diminishes slowly over time. For \(t \rightarrow \infty\), both \(x\) and \(\dot{x}\) go to zero.