5.2: Complex Solution

The variable \(x(t)\) is the displacement of the particle, so it ought to be real. However, a good way to solve the damped harmonic oscillator equation is to generalize \(x(t)\) to complex values. In other words, we convert the harmonic oscillator equation into a complex ODE: \[\frac{d^2 z}{dt^2} + 2\gamma \frac{dz}{dt} + \omega_0^2 z(t) = 0, \quad z(t) \in \mathbb{C}.\] The parameter-counting rule for real ODEs (see Chapter 2) generalizes to complex ODEs, but the parameters are now complex numbers. As the complex damped harmonic oscillator equation is a second-order ODE, its general solution must have two complex free parameters.

Let us now figure out how to obtain the general solution to the complex damped harmonic oscillator equation. Then we will see how to use it to solve the real problem.

Complex ansatz

To derive the general solution, first note that the damped harmonic oscillator equation is linear. If we have two solutions \(z_1(t)\) and \(z_2(t)\), then any superposition \[\psi_1 \, z_1(t) + \psi_2 \,z_2(t),\quad \mathrm{where}\;\, \psi_1, \psi_2 \in \mathbb{C}\] is also a solution. This can be verified by direct substitution into the ODE.

Therefore, a good strategy for obtaining the general solution is to find two specific solutions and superpose them. The two coefficients, \(\psi_1\) and \(\psi_2\), would then serve as the general solution’s two free parameters.

We can make a guess (or an ansatz) for a specific solution: \[z(t) = e^{-i\omega t}.\] Here, \(\omega\) is a constant to be determined (which could be complex). The first and second derivatives are: \[\begin{align} \frac{dz}{dt} &= -i\omega\, e^{-i\omega t} \\ \frac{d^2z}{dt^2} &= -\omega^2\, e^{-i\omega t}\end{align}\] Substituting these into the differential equation gives: \[\left[-\omega^2 - 2i\gamma \omega + \omega_0^2 \right] e^{-i\omega t} = 0.\] This equation holds for all \(t\) if and only if the complex second-order polynomial on the left-hand side is zero: \[-\omega^2 - 2i\gamma \omega + \omega_0^2 = 0.\] The solutions for \(\omega\) can be obtained from the quadratic formula: \[\omega = -i\gamma \pm \sqrt{\omega_0^2 - \gamma^2}.\] Hence, we have found specific solutions that involve complex frequencies: \[z(t) = \exp\big(-i\omega_\pm t\big), \;\;\mathrm{where}\;\; \omega_\pm = -i\gamma \pm \sqrt{\omega_0^2 - \gamma^2}.\] For each value of \(\gamma\) and \(\omega_0\), both \(\omega_+\) and \(\omega_-\) yield valid specific solutions.

Complex frequencies

What does it mean to have an oscillation with a complex frequency? If we write the real and imaginary parts of the frequency as \(\omega = \omega_R + i \omega_I\), then \[z(t) = e^{-i\omega t} = e^{\omega_I t} \; e^{-i\omega_R t}.\]

If both \(\omega_R\) and \(\omega_I\) are non-zero, this describes a spiral trajectory in the complex plane whose magnitude either increases or decreases with time, depending on the sign of \(\omega_I\). To see this explicitly, we can write \[z(t) = e^{\omega_I t} \; e^{-i\omega_R t} = R(t)\, e^{i\theta(t)}, \;\;\mathrm{where}\;\,\begin{cases}\displaystyle R(t) &= e^{\omega_I t}, \\ \displaystyle \theta(t) &= -\omega_R t.\end{cases}\] The real part of \(\omega\) determines the oscillation frequency, and the imaginary part determines whether the amplitude grows with time (amplification) or shrinks with time (damping). A positive imaginary part implies amplification, and a negative imaginary part implies damping; zero imaginary part (i.e., a real frequency) implies constant-amplitude oscillation.

Now let’s look at the complex frequencies appearing in the specific solutions to the damped harmonic oscillator: \[\omega_\pm = -i\gamma \pm \sqrt{\omega_0^2 - \gamma^2}.\] In the plot below, you can see how the position of \(\omega_\pm\) in the complex plane depends on the values of \(\gamma\) and \(\omega_0\):

Figure \(\PageIndex{1}\)

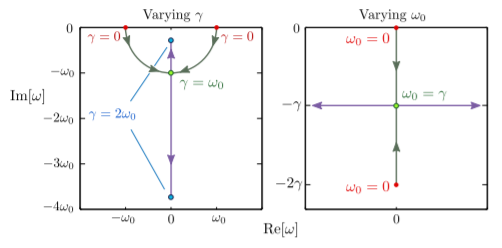
In particular, note the following features:

• For \(\gamma = 0\) (zero damping), the two frequencies are both real, and take the values \(\pm \omega_0\). This corresponds to simple harmonic oscillation at the oscillator’s natural frequency.
• If we increase \(\gamma\) from zero with \(\omega_0\) fixed, both \(\omega_+\) and \(\omega_-\) move downwards in the complex plane, along a circular arc. Since the imaginary part of the frequencies are negative, the particle undergoes damped oscillation. This is called under-damped motion.
• At \(\gamma = \omega_0\), the frequencies meet along the imaginary axis. This is the case of critical damping, which we will discuss in Section 5.3.
• For \(\gamma > \omega_0\), the two frequencies move apart along the imaginary axis. Purely imaginary frequencies correspond to a trajectory that decays without oscillating. This is called over-damped motion, which we will discuss in Section 5.3.