Innovative Teaching Techniques and U.S.-Developed Materials

INTRODUCTION

In common with many other universities, we recently introduced some innovative teaching techniques in two introductory physics courses at the University of Toronto [1]. These included Peer Instruction, Interactive Demonstrations, and Activity-Based Tutorials. For many of these, we used classroom-tested materials from U.S. universities, and found that they were often insufficiently challenging for our students. We hypothesize that this may be true generally of U.S.-developed teaching materials for Canadian students.

A recently published study by the National Center for Education Statistics at the U.S. Department of Education compared mathematical and scientific literacy of 15-year-olds from many countries [2]. Canadian young people fared much better than their U.S. counterparts. This is consistent with our finding that when these students are a bit older and enter university, they are better prepared than U.S. university students.

If our hypothesis holds up to scrutiny, the implication is not that innovative teaching techniques are unnecessary for Canadian students, but rather that their application will require more original Canada-specific development work than might have been anticipated.

THE COURSES

The two first-year courses which we discuss are Physics for the Life Sciences (PLS) and Foundations of Physics (FP). They are both calculus based and have Grade 12 physics and Grade 12 calculus as pre-requisites. They both have associated laboratories which do not directly track the material of the lectures.

PLS has over 1000 students. Serway and Jewett is the text [3]. It has a single lecture section, which meets in the university’s Convocation Hall. There are two lectures and one tutorial every week. For Peer Instruction and Interactive Demonstrations, we originally had students respond to questions with a show of hands. In mid-term we gave the students five squares of different colored poster board, which they raise to respond to a question. Participation in these activities is on the order of 75%.

FP is intended for students with considerable ability in physics and mathematics; it has about 130 students and uses Knight as the text [4]. This is a new book written by a strong proponent of innovative teaching methodologies. FP has a single lecture section, with three lectures and one tutorial every week. Most students have a Personal Response System (“clicker”) which they use to answer in-class questions [5]. The clicker was sold separately, but a rebate coupon was bundled with the textbook. Participation is on the order of 60%.

PEER INSTRUCTION

The leading proponent of Peer Instruction is Eric Mazur at Harvard [6]. Briefly, in place of a traditional lecture on a particular topic, a challenging conceptually-based multiple choice question is presented to the class. Mazur calls these questions Concept Tests. When a question is well-designed, a significant fraction of the class will initially fail to give the right answer. In this case, the class is divided into small groups who discuss the question and answers amongst themselves. After a few minutes the students individually vote again on the right answer. It is common for the percentage of students getting the right answer to go up dramatically after the Peer Instruction phase.

There are a number of positive things that occur when this process works. Perhaps one of the more important is that it engages the students with the material. Thus, we tried to insure that our discussion in class did not “give away” the right answer before presenting a question: we wanted a significant fraction of the class to initially get the wrong answer.

In Reference 6, Mazur supplies many Concept Tests that have been tested with his Harvard students. In addition, we have written some of our own questions, and have also used questions designed and tested by E.F. Redish at the University of Maryland [7] and still others by A. Sarty at St. Mary’s University in Halifax [8]. The Knight textbook also incorporates conceptual “Stop and Think” questions which we occasionally used directly.

Here is a ConcepTest by Mazur:

A train car moves along a long straight track.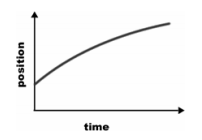

The graph shows the position as a function of time. The graph shows that the train:

1. speeds up all the time.

2. slows down all the time.

3. speeds up part of the time and slows down part of the time.

4. moves at a constant velocity.

Initially 80% of PLS students got this question correct. The situation was similar for FP students, who were presented with “Stop and Think” kinematics questions from the Knight text. More than 80% of FP students were able to “visually integrate” an acceleration vs. time graph to recover velocity, and then to perform a second visual integration to get position.

For Peer Instruction to work, when the class breaks up into small groups there should be disagreement within each group about the right answer. These questions, which work for Harvard students, were much too easy for our PLS and FP students.

Here is another ConcepTest by Mazur

A marathon runner runs at a steady 15 km/hr. When the runner is 7.5 km from the finish, a bird begins flying from the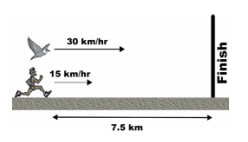 runner to the finish at 30 km/hr. When the bird reaches the finish line, it turns around and flies back to the runner, and then turns around again, repeating the back-and-forth trips until the runner reaches the finish line. How many kilometers does the bird travel?

1. 10

2. 15

3. 20

4. 30

5. I have no idea

This time almost all PLS students initially got the question correct, so as a basis for Peer Instruction it was another failure.

Not all questions were failures. Here is another by Mazur that half of PLS students initially missed:

Suppose Earth had no atmosphere and a ball were fired from the top of Mt. Everest in a direction tangent to the ground. The initial speed is high enough to cause the ball to travel in a circular trajectory around Earth. The ball's acceleration is: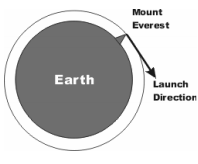

1. much less than g, since the ball doesn't fall to the ground

2. approximately g

3. dependent on the ball's speed

After Peer Instruction almost all the class knew the correct answer.

Here is a similar conceptual question given to the more advanced FP class:

The Space Station orbits 400 km from the ground. What is the value of g there?

(A) Same as g on the ground

(B) zero, as in “zero gravity”,

(C) 10% of g on the ground,

(D) 50% of g on the ground,

(E) 87% of g on the ground.

We can be more quantitative about the results when this question was presented to the FP class, because the student’s “clicker” responses were recorded. The results after the first vote were: (A) 18%, (B) 10%, (C) 20%, (D) 10% and (E) 42%. This broad spread signals considerable confusion, but a substantial fraction have guessed the correct answer, which is (E). After some discussion, we followed up with a calculation to show that (E) is most correct. The calculation illustrated the use of a binomial expansion to get the answer to lowest order in the ratio of station altitude to the radius of the Earth.

INTERACTIVE DEMONSTRATIONS

Although students love lecture demonstrations, often they don’t actually learn from them. They may be made more effective by asking the students to predict the result before doing the demonstration [9]. If a significant fraction of the student predictions are wrong, such an Interactive Demonstration can be combined with Peer Instruction.

We constructed an actual apparatus to use with the following question.

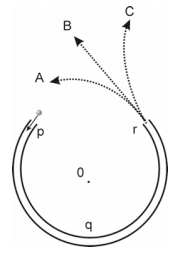
The figure shows a frictionless channel in the shape of a segment of a circle with the center at O. The channel has been anchored to a frictionless horizontal table top. You are looking down at the table. Forces exerted by the air are negligible.

A ball is shot at high speed into the channel at p and exits at r.

Which path in the figure would the ball most closely follow after it exits the channel at r and moves across the frictionless table top?

This question is from the Force Concept Inventory [10]. Used as a pre-test, many beginning physics students in the U.S. miss this question. In addition, Redish at the University of Maryland has also used this problem as the basis for an Interactive Demonstration, and reports that many of his students miss it too [11]. At the University of Toronto, the overwhelming majority of our PLS and FP students initially got the right answer.

As with the U.S. designed Peer Instruction questions, not all of the Interactive Demonstrations were too easy. Here is question for which we also constructed an apparatus [12].

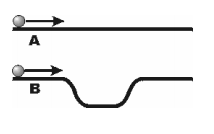Two balls are launched along a pair of tracks with equal velocities, as shown. Both balls reach the end of the track. Which ball reaches the end of the track first?

A.

B.

C: It will be a tie: they will reach the end of the track at the same time.

Initially about 1/3 of PLS students chose answer (A) and most of the remainder chose (C). After Peer Instruction, the class was nearly unanimous in choosing answer (C). Results at the University of Maryland are similar to ours. There was considerable discussion in class and in the following tutorial when the demonstration showed that the correct answer is (B).

In the FP class, the outcome was quite similar. The initial vote was: (A) 19%, (B) 9%, and (C) 72%. After this vote, the students were sufficiently provoked that several spontaneously defended their answers in front of the whole group. The class then broke into fairly heated discussion. After discussion, but before running the demonstration, they voted again and the results shifted only slightly: (A) 25%, (B ) 7%, (C) 65%. Once the demonstration had dramatically shown them to be wrong, many claimed to see the “trick” to the question. It still took considerable debate before a satisfying and correct explanation was verbally formulated. Students offered hypotheses as to why they had been fooled --- a rare example of students directly analyzing their own misconceptions. We followed up this class with a homework question which involved making a graphical analysis of the demonstration.

ACTIVITY-BASED TUTORIALS

Some data indicate that the greatest gain in conceptual understanding by students occurs by replacing the traditional tutorial/recitation sections with a group-learning environment based on conceptually based activities [13].

PLS introduced such activities for some tutorials, based on the McDermott workbooks [14]. These activities were developed at the University of Washington, Seattle, and there these materials are used after the lecture on the topic of the activity. We found that when we used the activities in this way they were much too simple and obvious for our students. When we used them to introduce the topic, before the class or reading assignment from the textbook, they were somewhat more successful, but only marginally.

FP used the Student Workbook that accompanies the Knight text for that course [4]. The results were similar. Students (and some teaching assistants) complained that the activities were too elementary and not enough like the end-of-chapter problems. In fact, our objective was exactly to avoid drilling the students on such standard problems. This anecdote illustrates the inherent conservatism of both students and teaching assistants, who, presented with the innovative materials, ask for the old familiar ones back. It is fair to say, however, that the new tutorial format works better than the old, in which teaching assistants solved problems in front of the class, who remained largely passive. Nevertheless, we find we must supplement the Workbook activities with more challenging material.

DISCUSSION

We believe that the methodologies we have introduced in our courses have had a very positive effect, both in terms of student performance and engagement with the material.

When a Peer Instruction question or demonstration was well formed, the atmosphere in the classroom is electric. In the smaller FP class, there is much more verbal feedback during class than in previous years. Students are noticeably more involved and less passive. In addition to this and other anecdotal evidence, there are some other data that confirm our conclusion.

First, in our tests we have disguised and repeated some conceptual questions from previous years. The improvement in student performance has been dramatic.

Second, PLS has a very active web log run by the Dept. of Biology. It has sections for first year courses in biology, chemistry, math, physics, psychology and anthropology. Teaching staff do not post to this blog but we do read it. The number of posts to the physics section is greater than biology, chemistry and math combined. Further, some of the discussion is far beyond the “who knows how to solve question X.Y?” and is now, half way through the academic year, including topics that are not part of the curriculum for the course [15]. We have not observed such behavior in previous years.

Developing questions and activities for these techniques requires a significant investment in time. When we decided to “jump off the cliff” and introduce them in our classes we thought that we could save a significant amount of effort by using the materials developed in the U.S. We have discovered that this was not entirely correct: the better preparation of our students makes a lot of the U.S. material too simple.

The task of developing more challenging materials to some extent anticipates the bigger task of carrying these innovative teaching techniques into the higher years. To date, almost all of the attention has been focused on entry-level, first year topics. Our experience indicates that we must broaden and deepen our approach to be successful with Canadian students. We cannot simply rely on the materials developed for the U.S. market.

The results of the study of 15-year-olds in Reference 2 may indicate that this situation is not a University of Toronto phenomenon. Canada-wide, our 15-year-olds are much better at science and math than their U.S. counterparts. It is reasonable to assume that this is also true for Canadian university students compared to U.S. ones.

REFERENCES

[1] Results of a Canada-wide survey will appear in A.J. Slavin, “Peer Learning in Large Lecture Sections”, Physics in Canada, forthcoming.

[2] U.S. Department of Education, National Center for Education Statistics. “Outcomes of Learning: Results From the 2000 Program for International Student Assessment of 15-Year-Olds in Reading, Mathematics, and Science Literacy”, NCES 2002–115, by M. Lemke, C. Calsyn, L. Lippman, L. Jocelyn, D. Kastberg, Y. Liu, S. Roey, T. Williams, T. Kruger, and G. Bairu. Washington, DC: 2001. A summary is available at http://nces.ed.gov/surveys/pisa/.

[3] R.A. Serway and J.W. Jewett, Jr., Principles of Physics, 3rd ed., Brooks/Cole, 2002.

[4] R.D. Knight, Physics for Scientists and Engineers with Modern Physics, Pearson, 2004.

[5] We use the ones by Hyper-Interactive Teaching Technology (H-ITT). The current generation of IR-based clickers can not handle the huge number of students in our PLS course.

[6] E. Mazur, Peer Instruction: A User’s Manual, Prentice Hall, 1997.

[7] Available on the web at http://www.physics.umd.edu/perg/role/PIProbs/.

[8] Private communication.

[9] See, for example, C.H. Crouch, A.P. Fagen, J.P. Callan and E. Mazur, Amer. J. Phys., 29, 835-838 (2004).

[10] D. Hestenes, M. Wells, and G. Swackhamer, The Physics Teacher, 30, 141-158, March 1992. It was revised in 1995 by I. Halloun, R. Hake, and E. Mosca, and this is very similar to question 6 of that version.

[11] Private communication. Redish also reports that after the demonstration many students claimed to have actually seen the ball follow trajectory A.

[12] We became aware of this question from Redish at the Univ. of Maryland, and cloned an apparatus built there. Diagrams of the apparatus are available at Reference 7. In addition, here is a link to a Flash animation of the question: www.upscale.utoronto.ca/PVB/H...cingBalls.html.

[13] E.F. Redish, Teaching Physics with the Physics Suite, Wiley, 101-102, 2003.

[14] L.C. McDermott, P. Schaffer and the Physics Education Group, Tutorials in Introductory Physics, Prentice Hall, 2002.

[15] There is currently an active discussion of the Least-Action Principle.