Chaos

James Gleick subtitled his popular book Chaos with Making a New Science. Note the word is "Science," not "Physics." The sub-title is quite reasonable. However, much of the work on chaotic systems occurs in Physics departments. This is a non-technical survey of chaotic systems. It is based on a one-hour class given largely unchanged to first year undergraduate Physics students, to upper year liberal arts students, and to upper year Physics majors and specialists. The emphasis is on the properties that all chaotic systems exhibit. A secondary emphasis is the fact that most work on these systems is impossible without computing technology.

The history of the study of chaotic systems exhibits a very common phenomenon in the sciences. When people began to study the systems we discuss below, they seemed utterly disorganized. Thus they were called "chaotic." As work progressed we discovered that hidden in the apparent disorganization was a great deal of structure. The structure shared by all of these systems then became the technical definition of these systems, which we continue to call "chaotic." So the technical meaning of chaos now means something quite different from the everyday meaning. Other examples of the same sort of phenomenon centers around words like energy, momentum, etc.

The Three Body Gravitational Problem

When Newton discovered (or "invented") the Universal Law of Gravitation, and invented (or "discovered") Newton's Laws of Motion, he then used these two discoveries to solve the problem of a planet such as the Earth in orbit around the Sun. Making the simplifying assumption that the Sun is fixed in space, the solution is that the orbit of the Earth is an ellipse. Our Earth's orbit is not as elliptical as the one shown; it is nearly circular. A little terminology: we can call the Sun an attractor of the Earth.

Later, Newton tried to solve the problem of two "Suns" and a single "Earth." To his surprise, he failed to find a solution to this second-simplest gravitational system. Through the years, others tried without success to solve this "three body problem." At one point a cash reward was offered for its solution: no one ever claimed the prize.

By the 1960's, it was realized that even if, for whatever obscure reason, we were having difficulty in analytically solving this problem, we could get approximate solutions using computers. The idea is fairly simple:

1. We know the position and velocity of the Earth at some time. We can calculate its acceleration using Newton's Laws.
2. That allows us to calculate the new position and new velocity of the Earth at some time a very very small "time step" later. We calculate its new acceleration using Newton's Laws.
3. We can the calculate the new position and new velocity at a very very small time later then the time in step 2.

We can continue this as long as we wish. Note that the solutions will not be perfectly accurate, but if we make the "time step" small enough we can make them as close to correct as we wish. Note also that in principle these calculations could be done by hand, but in practice such a scheme is highly impractical.

Here is the result of such a calculation. We assume that the "Suns" are actually point particles so the "Earth" never collides with them. The Earth starts at a position between the two Suns that is below and slightly to the right of the midpoint; it is initially slowly moving up and to the right.We have solved from the initial time 0 to a time 80 units later. Note that being able to solve this three-body problem analytically would be equivalent to finding a mathematical expression for this curve; this leads us to suspect, correctly, that an analytic solution to the problem is not possible. It is possible to show that the trajectory of the Earth will never repeat itself even if we let the time go to infinity. This, in turn, leads to the idea that the trajectory after infinite time is an infinitely long line in a finite volume. This simple gravitational system is our first example of a chaotic system.

Figure 3: This is an animation of the three-body gravitational problem with two fixed "Suns" and one "Earth".Technical note: the three body problem above was solved in a Hamiltonian formulation, using Mathematica's NDSolve function. The units are such that GM = m = 1, and the two Suns are 2 units apart.

It is important to stress that this, and all classical chaotic systems, is completely deterministic. If we start the Earth with identical position and velocity, it will follow exactly the same trajectory each and every time. There are, however, quantum chaotic systems, and quantum systems are usually considered to be non-deterministic.

Next, we consider solving the same three body problem that we have just done with one minor difference. In Figure 3, the horizontal speed of the Earth at the beginning was 0.00500. We re-solve the problem with the initial horizontal speed that is one percent larger: 0.00505. The initial position and the initial vertical speed are exactly the same as before. We solve this problem for a final time of 15 units (green curve) and compare to the previous system (magenta curve) with a final time also of 15 units (Figure 4).

Figure 4: This is an animation of two solutions to the three-body gravitational problem which differ only in that their initial horizontal speeds were different by one percent. Initially, the two "planets" track each other almost perfectly, so you can only see one of them. Later the trajectories diverge. When the animation is finished, it starts again from the beginning.

To the right we show two solutions to the three body problem. They both start from the point that is horizontally about half-way between the two suns and is below the line connecting the suns. The previous solution that we have been looking at is the upper (red) trajectory. The lower (green) trajectory differs only in that its initial horizontal speed is one percent greater than the upper red one. Looking carefully, we can see that at the beginning the two trajectories match fairly closely. Later, however, the two trajectories diverge. We have an animation of the time evolution of these two trajectories, where the second image is on top of the first one. It shows the differences between the trajectories much more clearly.

Sensitive Dependence on Initial Conditions

From the animations, we see that initially the two trajectories are almost exactly the same; this is what we would expect for non-chaotic systems. Suddenly, the two trajectories radically diverge. This radical divergence arising from miniscule differences in the initial conditions is called Sensitive Dependence on Initial Conditions (SDIC), and is a characteristic of all chaotic systems. Sometimes it is called the "butterfly effect" because, if history were chaotic, then whether or not a particular butterfly landed on a particular flower in the Himalayan mountains in 1837 determined the outcome of World War II.

Many workers in the field take SDIC to be the primary indicator of a chaotic system. In any case, we shall place it as the first entry in the list we are building of the properties of all chaotic systems:

• All chaotic systems exhibit Sensitive Dependence on Initial Conditions.

Above, we saw another phenomenon that turns out to be shared by chaotic systems.

• For all chaotic systems, the trajectory never repeats.

Here is an example that is much-studied by researchers into chaotic systems. We imagine a big hopper of sand, and we drop one grain of sand at a time onto the floor. A sandpile begins to form. The key feature here is that the height of the sandpile goes up as the number of grains of sand that are dropped onto it increases. The exact relationship between the height and the number of grains of sand depends on factors such as how the grains pack together in the sandpile etc. We call such a situation linear.Prof. Jim Drummond (U. Toronto) describes a linear system this way:

"If I kick it, it screams. If I kick it harder, it screams louder."

In this context, the height does not have to vary directly as the number of grains of sand. It might go up as the square root of the number of grains, or the square. The crucial point is that height goes up smoothly with the number of grains of sand. At some point the sandpile gets so high that when we drop one more grain of sand onto it, an avalanche occurs and the height of the sandpile is reduced. There are two things to note about this:

1. A small change in the input, one more grain of sand, has caused a huge change in the output, the height of the sandpile. Thus, the system is exhibiting Sensitive Dependence on Initial Conditions.
2. The system is now nonlinear. The output is not proportional to the input.

This last point, too, is shared by all chaotic systems. So we have another entry in our list of properties shared by all chaotic systems.

• All chaotic systems are nonlinear.

We will be adding to this list in subsequent sections.

The Logistic Map

Imagine we are trying to model the population of, say, rabbits in a forest. We know that, given what rabbits like to do, the increase in population of rabbits will be related to the number of rabbits that we have. So we expect a term to look something like:

number(next generation) = L * number(this generation)

Here L is a constant representing the fecundity of the bunnies.

We also know that when there are too many bunnies in the forest then lack of food, overcrowding, etc. will suppress the number of bunnies in the next generation. If at a population of 100,000 all the bunnies die, then we need a term like:

n(next generation) = 100000 - number(this generation)

Putting these two terms together we get:

number(next generation) =
L * number(this generation) * (100000 - number(this generation))

This equation is called the Logistic equation. It is so over-simplified that it has nothing to do with the actual dynamics of how a population of bunnies (or much of anything else) changes. We will see further examples later of systems that get over-simplified to the point that they have virtually no physical content, but nonetheless teach us important lessons about chaotic systems.

Say we start with two thousand bunnies, and that the constant L is 0.000028. Then it is simple to calculate that the next generation will have 0.000028 * 2000 * (100000 - 2000) = 5488 bunnies. The next generation after that will have 0.000028 * 5488 * (100000 - 5488) = 14523 rabbits, and so on. We can make a graph of the total number of rabbits in the population. We see that there are some initial small oscillations, but eventually the population settles down to a constant value of 64285.

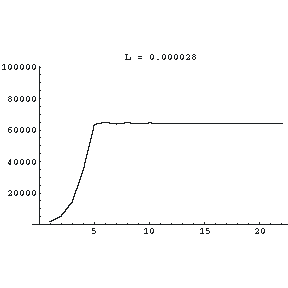
Say we start with two thousand bunnies, and that the constant L is 0.000029. We see that there are some initial somewhat larger oscillations, but eventually the population settles down to a constant value of 65,517. So increasing L increases the steady state number of rabbits in the population.

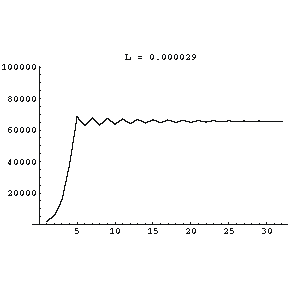
If we increase the fecundity of the rabbits by setting L to 0.000031, something very interesting happens. The population bifurcates and in the "steady state" oscillates between two different values.

Some ecologists now believe that such a "boom-bust" ecological system is better than a stable one.

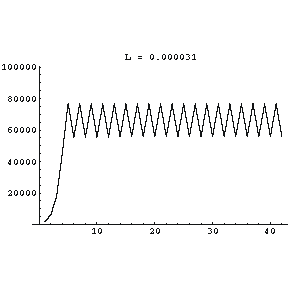
Increasing L to 0.000032 increases the size of the swings in the population.

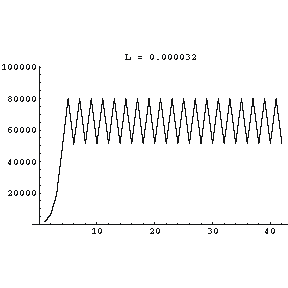
At L equal to 0.000035 the bifurcated population values have bifurcated once again, and the number is now oscillating between four different values!

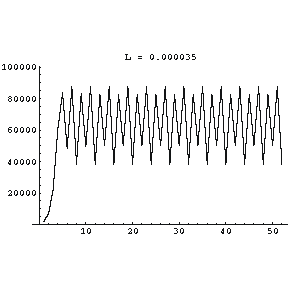
At L equal to 0.0000395 the population values are weird. In fact, the system has now become chaotic. This means that it exhibits all the properties of all chaotic systems. For example, a miniscule change in the initial number of rabbits leads to radical changes in the number of rabbits in each succeeding generation. It also means that the trajectory shown to the right never repeats no matter how many generations we calculate in the graph.

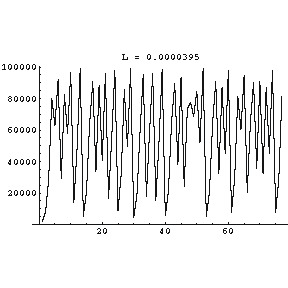
Technical note: in the numerical examples discussed above, I rounded all numbers to the nearest integer.

I have written a simple Flash animation to investigate the Logistic Map further. The animation is available here.

To study the map in more detail you may wish to look at a little web-program that I wrote: it is available here.

In addition, John McDonald wrote a Java applet this also explores the behaviour of this system. There are two sites that I know of running it: www.geom.umn.edu/~math5337/ds...Iteration.html andhttp://www.enm.bris.ac.uk/staff/hinke/courses/Chaos/applets/iteration/Iteration.html; in terms of our discussion, it measures populations in 100 kilo-bunnies with 50,000 rabbits in the first generation.

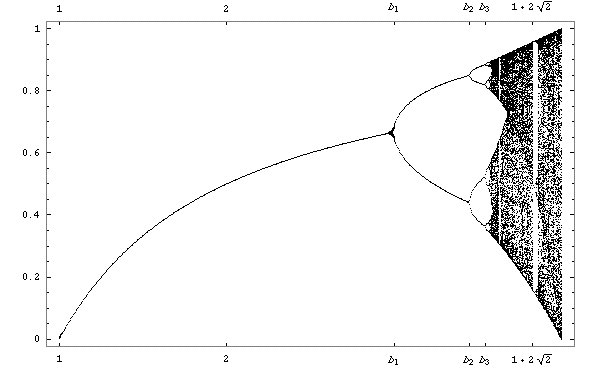
We can calculate the "steady state" values of the population as a function of the fecundity factor L, and the result of such a calculation is above. The graph is called the Logistic Map. We see that initially, as the value of L increases, so does the size of the population. Then we see the first bifurcation of the population, followed by the second, and finally the transition to chaos. There are islands of stability for some higher values of L. We also see a hint in the figure that after the second bifurcation, yet another bifurcation occurs; this in fact occurs. If we zoomed in on the region just before the first transition to chaos, we would see further levels of bifurcation occurring. In fact, it can be shown that these bifurcations occur to an infinite level. This leads us to our next indicator of chaotic systems:

• For all chaotic systems, the transition to chaos is preceded by infinite levels of bifurcation.

Much of the early work on the logistic equations was done by physicist Mitchell Feigenbaum in the mid-1970's. At this time Feigenbaum's "day job" was at the Los Alamos National Laboratory. He was using the then-new Hewlett-Packard HP-65 hand-held programmable calculator to compute when the next bifurcation in the population would occur as L increased. The HP-65 was wonderful for its day, but now would be considered suitable only for use as a paperweight. It was so slow that Feigenbaum had lots of time on his hands waiting for it to do its calculations. He began trying to guess the value of L for which the next bifurcation would occur.

This led him to discover that the rate at which the bifurcations were occurring was governed by a constant number. If, say, L(n) is the value of L for which the n-th bifurcation occurs, and L(n + 1) is the value where the next bifurcation occurs, then at all levels L(n + 1) divided by L(n) is always the same value. It turns out that this number, now called the Feigenbaum number, is irrational and approximately 4.6692016090... It also turns out that the Feigenbaum number is associated with all chaotic systems.

• For all chaotic systems, the infinite bifurcations preceding the transition to chaos are characterised by the Feigenbaum number.

When one is dealing with circles, it is essentially impossible to avoid having to deal with the irrational number pi, whose value is approximately 3.1415926... This number seems to be intrinsically associated with circular systems and/or the way our minds think about them. Similarly, when one is dealing with systems where the amount of change in some parameter depends on the value of that parameter, the irrational number e keeps showing up in, for example, natural logarithms or exponential growth or decay. So e, whose value is approximately 2.71828..., is somehow associated with these systems and/or the way our minds think about them. These two numbers are pretty mysterious, although many of us have gotten used to dealing with them. Now we seem to have a third such number, this time associated with all chaotic systems: the Feigenbaum number.

The Lorenz Attractor

In the early 1960's Edward Lorenz was modelling weather systems at M.I.T. He developed a set of equations that might describe turbulence in the upper atmosphere, but to his surprise could not succeed in solving the equations. He began simplifying the equations, until he finally ended up with a set of equations that no longer had any possible relevance to the problem of turbulence. Just for reference, here are those equations:

\[\dfrac{dx}{dt} = s (x - y)\]

\[\dfrac{dy}{dt} = -xz - y + r x\]

\[\dfrac{dz}{dt} = x y - b x\]

Here \(x\), \(y\) and \(z\) are variables and we will think of \(t\) as being the time; \(s\), \(r\) and \(b\) are constants.

Lorenz could not solve these simple equations either. However, the equations can be approximately solved with a computer using exactly the same technique we discussed above for the three body gravitational problem. The result of such a calculation giving the trajectory {x,y,z} as time evolves is shown in Figure 5.

Figure 5: The Lorenz Attractor. A sample solution in the Lorenz attractor when ρ = 28, σ = 10, and β = 8/3. (CC SA-BY 3.0; Dan Quinn)

We see that this "attractor" has two points that attract the trajectory. This is similar to the three body gravitational problem we looked at above. In the early days of studying this Lorenz attractor everything about it seemed strange; thus it is sometimes called the strange attractor. Now, we know that although it is strange, the many many chaotic systems that have been discovered are similarly strange.

This is yet another chaotic system, and thus has all the properties of such systems. We have a simple animation of this solution in which we rotate the trajectory; it shows the "three dimensional" nature of the trajectory more clearly. To see the animation click here.

We have also prepared a Flash animation which allows you to use the mouse to change the view of the attractor. It requires the Flash player of version 6 or better, and the file size is 550k. It will appear in a separate window. To view the animation click here .

We see that the trajectory around each attractor is approximately in a plane. The two planes about the two attractors are almost but not quite in the same plane. In fact, we describe the dimensionality of the Lorenz attractor as being just a bit larger than two. This non-integer or fractional dimensionality turns out to be another characteristic of chaotic systems. Sometimes such objects are sometimes called fractals.

All chaotic systems exhibit fractional dimensionality.

Technical note: the above solution to the Lorenz equations had initial positions of x = 0, y = 1 and z = 0. The constants were r = 28, s = 10, and b = 8/3. The time t goes from 0 to 2048. Not all solutions of the Lorenz equations are chaotic; the crucial factor is the value of the constant r.

I have already mentioned that this document is based on a one hour class given essentially unchanged to undergraduates at a variety of levels. The remainder of this section is a little more technical than the rest, and for some contexts I instead expand on the idea of fractional dimensionality. A brief document outlining that presentation is available in html here and in pdf here. All versions of the class end with the Further Discussion and Conclusions section at the end of this document.

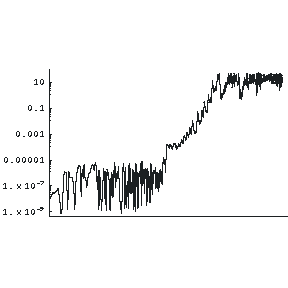
As we have just stated in the technical note, the above solution was generated with the initial value of y equal to exactly one. We calculate a second solution with the initial value of y = 1.000000001. We then make a plot of the distance between these two trajectories as a function of time; this plot appears to the right.

We see that, just as for the three body problem, initially the distance between the two trajectories is fairly small. Then, at some point they diverge rapidly. This graph is called a Lyapunov plot. Technically, you may wish to know that it is a log-log plot.

You can see that when the two trajectories begin to diverge, the distance between them as a function of time is almost exactly a straight line. This, too, is a property of all chaotic systems.

• For all chaotic systems, a Lyapunov plot of the distance between trajectories versus time will exhibit a straight line.

Say we take one of the solutions to the Lorenz equations, and plot where the trajectory crosses the x-y plane when the value of z is 20 and increasing. This is called a Poincaré section, and is shown to the right. The section is a way of analyzing complex motion by reducing the amount of information we need to deal with all at once.

Poincaré introduced this display in the late nineteenth century while he was working on the three body gravitational problem.

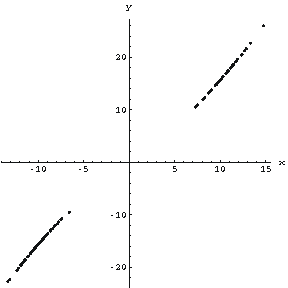
For the Lorenz attractor, all the variables, such as z, go through maximum and minimum values as the trajectory cycles around the attractors. We can make a plot of the value of a particular maximum value of z versus the value of z for its previous maximum. This is called the first return map and is shown to the right. Also shown is a dashed line which is at an angle of exactly 45 degrees with the horizontal. We see that the points in the return map are initially increasing and all lie above the dashed line. This is yet another characteristic of chaotic systems.

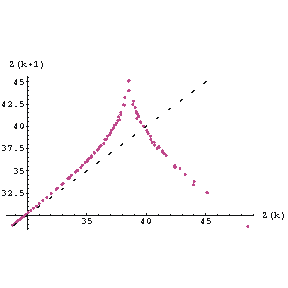
For all chaotic systems, the initial points of the first return map always lie above a line making an angle of 45 degrees with the horizontal.

Further Discussion and Conclusions

Above we have discussed three chaotic systems. We now know that there are many many systems that can become chaotic. A few examples include:

1. A pendulum whose support point is oscillating up and down.
2. A double pendulum.
3. A dripping faucet.
4. A billiard ball on a perfectly reflecting billiard table with two parallel sides connected by two semicircles. This is called a Bunimovich stadium. A Flash animation of the stadium is available here

For physicists who, like me, were educated in a more-or-less traditional way, we were tacitly taught that we were going in a straight line from ignorance to understanding. In retrospect, our path was not even close to straight, as we had to avoid the swamps and craters of chaos that appear nearly everywhere we look. Previously we had to avoid those swamps and craters because they are often not analytically solvable, and solving problems analytically used to be our only major technique. For some other systems, such as the logistic equations, solvability is not an issue; the calculational requirements, however, largely preclude their study with only a pencil and some paper. Computers have allowed an explosion in our understanding of chaotic systems in the past 35 years or so.

Virtually alone, in the late nineteenth century Poincaré realised some of the magnitude of the problems with the three body gravitational problem, and found some unique and creative ways to nibble around the edges of the problem. These techniques are still in use today in the study of chaos.

We have discussed some but not all of the properties that all chaotic systems share. These include:

• Sensitive Dependence on Initial Conditions.
• The trajectory never repeats.
• They are nonlinear.
• The transition to chaos is preceded by infinite levels of bifurcation.
• The infinite bifurcations preceding the transition to chaos are characterised by the Feigenbaum number.
• Fractional dimensionality.
• A Lyapunov plot of the distance between trajectories versus time will exhibit a straight line.
• The initial points of the first return map always lie above a line making an angle of 45 degrees with the horizontal.

Thus, hidden in the apparent disorganization is a great deal of structure. Lorenz has recently stated that he believes that the weather is a chaotic system. Since it is virtually impossible to know the initial conditions, i.e. the temperature, density, wind, humidity, etc., with perfect accuracy, Sensitive Dependence on Initial Conditions implies that a long-range weather forecast is impossible in principle. Lorenz speculates that "long range" here means a week or more.

Earlier I made a brief reference to the fact that most interpretations of Quantum Mechanics believe that quantum systems are nondeterministic. This is, of course, where Einstein bailed out on Quantum Mechanics, stating that "God does not play dice with the universe." Bohr replied to Einstein "Quit telling God what to do!"

A recent re-interpretation of Quantum Mechanics by David Bohm and his group introduces the notion of a quantum potential. This potential is non-local, which accounts for some of the strange "influence at a distance" that Quantum Mechanics predicts and that has been experimentally confirmed. But in Bohm's interpretation the motion of objects such as electrons going through an array of slits is governed by this quantum potential and the trajectory turns out to be chaotic. Thus to Bohm quantum systems are another deterministic chaotic system. Finally, there is a wonderful free program for studying and playing with chaotic and fractal systems. It is called fractint.You can learn more about this program at spanky.triumf.ca/www/fractint/fractint.html.