High Energy Physics

In the conventional view, "stuff" is made of atoms. The atoms are made of electrons, protons and neutrons. High Energy Physics deals with the question of what the electrons, protons and neutrons are made of. It is called "high energy" because experimentally one needs very high energy probes to try to take these "elementary particles" apart. This document is an overview of high energy physics at a non-technical level. Some of the material presented is decidedly not traditional for an overview of High Energy Physics.

FEYNMAN DIAGRAMS

Classically, we describe electron-electron scattering in terms of an electromagnetic field caused by one electron which causes a force on the second electron. The second electron similarly causes an electromagnetic field which causes a force on the first electron. Of course, we know that this field has a complementary particulate aspect, the photon. Below a spacetime diagram for electron-electron scattering in this particulate view.

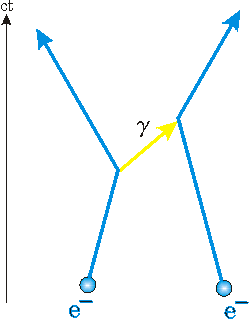
The electron on the left emits a photon, labeled, which is then absorbed by the electron on the right. The fact that such a series of events causes both electrons to change their state of motion is a pure quantum effect. According to Quantum Mechanics, when two object exchange an object, a Quantum Exchange Force exerts a force on both objects. When the object being exchanged is a photon, the interaction is electromagnetic. This diagram has two vertices, which are the points where the electron worldlines have a kink and the photon worldline connects at the kink.

Although the above is the simplest possible interaction between two electrons exerting electromagnetic forces on each other, it is not the only possible interaction. For example, below two more possible mechanisms. The upper figure shows the exchange of two photons, and the lower one of three photons.

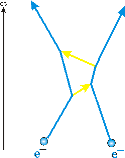
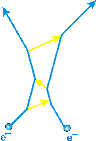
In the 1950's Richard Feynman and Julian Schwinger realized that the total electromagnetic interaction between two electrons is just the sum of all possible interactions. Each of the above spacetime diagrams represent some Quantum Mechanical wave function amplitude, and to get the total amplitude just add up all the terms. The fact that there are an infinite number of diagrams, each of increasing complexity, turns out not to be a problem, because the more vertices in the diagram the smaller its contribution to the total wave function.

This is very similar to the set of sums of numbers such as:

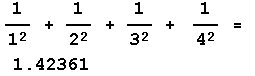
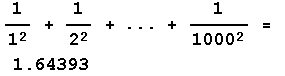
In fact, the mathematicians have shown that if the above sum is extended to an infinite number of terms, the value of the sum converges to an irrational number whose value is approximately 1.64493. Similarly, the infinite sum of spacetime diagrams for electron-electron scattering converges to a finite value.

Another example of an infinite sum of numbers equal to a finite value can be seen in a little Flash animation. It has a size of 12k, and will appear in a separate window. To access the animation click here.

The physical interpretation of this approach to electrodynamics is that when a pair of electrons in some initial state scatters so they end up in some final state, they get there via every possible path. Recall that the Quantum Mechanical description involves the wave function or state function, which in conventional interpretations represents some sort of partially unmanifested level of reality; a good analogy is the Aristotelian concept of potentia. Here the infinite number of diagrams connecting the initial and final states become an infinite number of wave functions, each representing a mechanism to get to the final state.

If you think again about the double slit experiment for electrons, when we see the interference pattern we know that the wave function was non-zero at both of the slits. Thus in some sense we can say that the electron got from the electron gun to the observing screen by going through both slits. Both paths from the gun to the screen have non-zero wave functions.

Recall Feynman's theory of antimatter being regular matter going backwards in time. Thus if we reverse the direction of the arrow heads, as shown, the same Feynman diagram describes positron-positron scattering.

This shouldn't be a big surprise if you remember that two negatively charged objects like electrons repel each other exactly like two positively charged objects like positrons.

Further reflection may convince you that as a consequence, we need not include arrowheads at all on the worldlines of objects represented in these diagrams. Similarly we need not include a time axis. For example, the diagram shown to the right is essentially identical to the first diagram we looked at above if we take the first diagram and reverse the direction of the time axis (and stand on our head to look at it!).

When we drop the arrowheads on the worldlines and drop the time axis entirely, we call these spacetime diagrams Feynman diagrams.

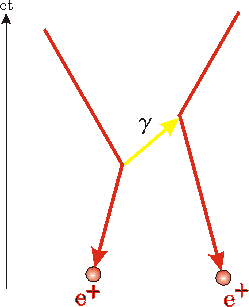
If we don't have to put arrow heads or time axes in Feynman diagrams, then what about interpreting the above diagram as having time flow from left to right? Then it is describing an electron-positron pair annihilating into a photon, and the photon later creating an electron-positron pair. And in fact, it is believed that this interpretation as well as all the other interpretations of this diagram is correct also.

So, pair production and annihilation is described by exactly the same mechanism as everyday electron-electron scattering.

Consider an electron interacting with all the other electrons in the universe: it experiences forces caused by the other electrons and in turn exerts forces on them. For the Feynman diagram describing the effect of the other electrons, the "propagators", the worldlines of the photons, lie along the light cones connecting the electron to other electrons which lie in the past. Similarly, the electron causes electromagnetic forces on all other charged bodies in the universe, and these propagators lie along the light cone from the electron at the present to charged bodies at times in the future.

However, we have just argued that the direction of time is irrelevant in these Feynman diagrams. Thus we can say that the forces exerted on the electron have two causes: the interactions from the past the the interactions from the future! Technically, these two causes are called the retarded and advanced potentials respectively. Similarly, the electron exerts forces on electrons in the past as well as the future.

Wheeler and Feynman commented in 1949:

"Generalizing, we conclude advanced and retarded interactions give a description of nature logically as acceptable and physically as completely deterministic as the Newtonian scheme of mechanics. In both forms of dynamics the distinction between cause and effect is pointless. With deterministic equations to describe the event, one can say: the stone hits the ground because it was dropped from a height; equally well: the stone fell from a height because it was going to hit the ground." Reference: J.A. Wheeler and R.P. Feynman, Rev. Mod. Phys. 21, (1949) 425.

Fred Hoyle and J.V. Narlikar have speculated that the direction of time's arrow may be related to the expanding universe via Wheeler and Feynman's acausal electrodynamics:

"We want to see how an arrow of time can emerge from this apparently time-symmetrical description. If we consider each separate particle, we give equal importance to advanced and retarded solutions. Where can the asymmetry come from? The asymmetry would normally come in this case from the asymmetry of the universe. The [light] cone in the future is different from that in the past. The distribution of the particles, the density, and so forth, in the future is in general different from the distribution in the past, and therefore it is not unlikely that when we perform the summation [over particles] we may find an asymmetry." - Reference: In T. Gold, ed., The Nature of Time (Cornell, 1967), pg. 25-26.

So far in this section, we have been describing the use of Feynman diagrams to describe the quantum aspect of the electromagnetic interaction. Technically this description is called Quantum Electrodynamics, and Feynman and Schwinger were awarded the Nobel Prize in Physics in 1964 for its development. Quantum Electrodynamics is one of our most successful theories. This is because the predictions that it makes can be experimentally tested to 10 or more significant figures, which is incredible precision and accuracy for any experiment, and so far the predictions agree with the experiments.

If the photon is the intermediary for the quantum exchange force that we call the electromagnetic interaction, what about the other interactions? Yukawa asked himself exactly this question about the strong force that holds the nucleus together in the 1930's. We know that, in contrast to the electromagnetic force, the strong force is short range: when two, say, protons get an appreciable distance away from each other the strong force becomes negligible and the electromagnetic one dominates causing them to repel each other. In 1935 Yukawa proposed that the particulate aspect of the strong field was a new "elementary particle" and in order for it to produce a short range interaction it must have a non-zero rest mass.

This strong force intermediary is now called the pi meson or pion. It was discovered in 1947 in cosmic rays by Lattes using a cloud chamber. Sometimes the intermediary of the strong force is given a more generic name: a gluon.

If one tries to use the Feynman diagram approach to describing these strong interactions, it turns out that the more vertices in the diagram the larger the value. Thus, as opposed to quantum electrodynamics, the sums do not converge to a finite value. This means that this approach to the strong interactions is mathematically intractable.

It is believed that there are massive W and Z particles which are responsible for the weak interaction.

Finally, people have proposed a graviton as the particulate intermediary of the gravitational interaction. This is one of many attempts to merge General Relativity and Quantum Mechanics. Sadly, as with all such attempts, it has been a failure.

ELEMENTARY PARTICLE PHYSICS

Many people believe that the field of "High Energy Physics" is the same as the field of "Elementary Particle Physics." Note that this belief assumes that there really are elementary particles in the universe: I think that this prejudges the whole question.

The proton and neutron are examples of nucleons, the type of particles found in the atomic nucleus. It turns out that there are hundreds of different nucleons, all of which but the proton and neutron almost instantaneously decay into a nucleon with less mass. The final stage in these decays is the proton, which so far as we know is stable. A free neutron will decay into a proton, but in stable nuclei it does not decay. The higher mass nucleons are sometimes called resonances.

There are also hundreds of different kinds of mesons.

To produce these high-mass nucleons and mesons, just take a very high energy electron beam such as can be produced by a super-strength electron gun and bang the beam into a block of matter. All these objects come streaming out. In the late 1960's new particles were discovered almost weekly. This approach has been compared to taking a watch, busting it into bits with a hammer, and then looking at the bits to try to figure out how the watch worked.

The remainder of this section on Elementary Particle Physics is divided into some perhaps surprising sub-sections:

• The Quark Model
• Ancient Greek Atomism
• Platonic Classifications
• The Sankhya Hindus
• Conclusion

The Quark Model

If there are photons, electrons, nucleons and mesons, plus a few more so-called elementary particles, it is natural to ask what they are made of.

The conventional answer is that photons and electrons are not made of anything, that they really are elementary. The conventional answer is also that mesons and nucleons are made of quarks. The quark model was proposed by Gell-Mann and, independently, Zweig in 1963.

Originally there were three kinds of quarks, called up, down, and strange, plus their corresponding anti-particles. Now three more quarks are proposed, named charm, bottom, and top. The names are the quarks are not intended to imply the nature of the quarks or their properties. The magnitude of the electric charge of the quarks is either 1/3 or 2/3 of the charge of the electron, and can be positive or negative. The nucleons are made of three quarks, and the mesons are made of a quark-antiquark pair.

All quarks are also believed to carry an additional property, called color. There are three possible colors for quarks in this view.

The next logical question might be of what are the quarks made? So far, the answer seems to be nothing: the quarks and the electrons are truly elementary particles in this view. If a substructure to quarks is ever discovered I propose calling those objects smitherons, whose plural is of course smithereens!

Immediately after the quark model was proposed, experimentalists began looking for them. They looked in cosmic rays, nuclear decays, cyclotrons, oysters (true!), basically everywhere they could think of. However, all the attempts ended in failure. So finally, believers came to the conclusion that we can't have an independent single quark, that they are "confined" inside the nucleons and mesons.

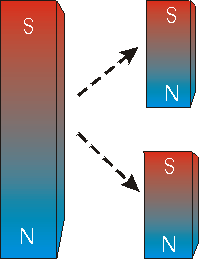
A rough analogy involves magnets. As you may know, magnets have a "North" and "South" pole. If we cut a magnet in half, as indicated to the right, we end up with two little magnets, each with a North and South pole. We have never observed a North or South magnetic pole separate from its opposite pole. Thus if these magnetic monopoles exist, they too are confined.

We shall call quarks a type of parton, by which we mean that they are a part of something else. So the quark model is an example of a confined parton theory.

Recall that according to the quark model, the nucleons are made of three quarks, while the mesons are made of quark-antiquark pairs. Thus, we can represent nucleon-nucleon scattering via the strong interaction by a Feynman diagram similar to that shown to the left. The worldlines are for the quarks.

Analyzing strong interactions in this way is called Quantum Chromodynamics. The similarity of the name to the wildly successful Quantum Electrodynamics of Feynman and Schwinger is obvious, while the 'Chromo' part refers to the fact that quarks have color. Spiff name or not, in my opinion so far the success of this approach has been under-whelming.

Ancient Greek Atomism

Democritus and Epicurus (4th - 5th century BCE) also believed that the world was made of atoms. The theory is fully described by Lucretius in De Rerum Natura.

The word atom means literally that which can not be divided. Lucretius also used the word elementa to describe them; the word also means the letters of the alphabet. This is sort of interesting since Needham in his classic multi-volume study Science and Civilisation in China has speculated that only cultures with alphabetic written languages develop atomistic theories (Volume 4, pg. 13). We shall see in the next section, for example, that the Chinese, who do not have an alphabetic written language, analysed the world into five elements but those elements are definitely not atoms.

Democritus describes an atomistic worldview in a famous statement:

"By convention sweet is sweet, by convention bitter is bitter, by convention hot is hot, by convention cold is cold, by convention color is color. But in reality there are atoms and the void. That is, objects of sense are supposed to be real and it is customary to regard them as such, but in truth they are not. Only the atoms and the void are real"

Lucretius' writing is pretty dense, but notice his discussion of least parts:

"The first principles, then, are solid and simple; they consist of least parts tightly compacted and compressed - not compounded by the coming together of these parts, but rather enduring in everlasting simplicity; from them nothing is permitted to be torn away or diminished, by nature which preserves the seed of things."

In 1977, Julia H. Gaisser and T.K. Gaisser wrote that the least parts that Lucretius writes about are a confined parton just as are the quarks. They also suggested that the reason for the need for confined partons in atomistic theories is that there is "an inherent conflict between the intuitive notion of infinite divisibility and the idea of discrete fundamental atoms of matter." (Reference: American Journal of Physics 45, (1977) 439.)

Platonic Classifications

Plato, of course, was not an atomist. He did, however, accept Empedocles' notion that there are four fundamental elements: air, earth, fire and water. He also knew that there are five and only five regular convex polyhedra each of whose faces are all identical: the tetrahedron, cube, octahedron, icosahedron and dodecahedron. In his one work on science, Timaeus, Plato associated four of these polyhedra with the four elements.

Tetrahedron: four faces, fire	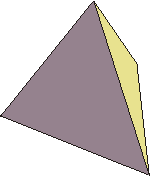Cube: six faces, earth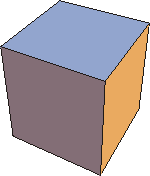
Octahedron: 8 faces, air	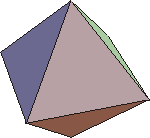Icosahedron: 20 faces, water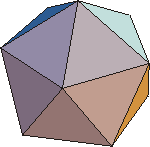

The fifth regular polyhedron, the 12 faced dodecahedron, "divinity employed in the fabrication of the universe."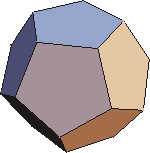

Plato used this scheme to explain how the elements "are able from certain dissolutions into each other to become the sources of each other's generation." He constructed the faces of the polyhedra from two types of right triangles, isosceles and 30-60-90 degrees. However, even without taking the faces apart into these triangles we see that:

2 air=2 octahedra=2 x 8=16 triangular faces.

1 fire=1 tetrahedron=1 x 4=4 triangular faces.

Thus, 2 air plus 1 fire=16 + 4=20 faces=1 icosahedron=1 water

Thus, we can do a Platonic form of chemistry.

However, consider the triangles that make up the faces. They are only two dimensional, and thus can not be true bodies. As Plato wrote, "In the first place, then, it is of course obvious to anybody that fire, earth, water, and air are bodies; and all body has depth."

The triangles in this classification are clearly partons, and since they are only two dimensional they can not exist separate from the thing of which they are a part. Thus they too are a type of confined parton.

This system of Plato's had a profound effect on Heisenberg, who read Timaeus as a young teenager.

The Sankhya Hindus

Hindu philosophy evolved an account of cosmic evolution, the Sankhya system, that had both continuum and atomistic aspects. Although some of the concepts can be traced back to the Upanishads and even the Rigveda, the oldest Sankhya text now available is the Sankhyakarika, which probably dates from the 5th century A.D.

The Sankhya idea was that there were five perceptible gross elements, the bhutas:

1. Ether (akasa) - ubiquitous, all-pervading, capable of vibration and sound.
2. Air (vayu) - light, cold, dry.
3. Fire (tejas) - light, hot, dry, luminous.
4. Water (apa) - liquid, cold wet.
5. Earth (kshiti) - heavy, hard, dense.

The bhutas were composed of actual atoms, called paranus.

Initially, the universe was a formless undifferentiated invisible ground, the prakriti. The prakriti was composed of a completely homogenous mixture of three "reals" called the gunas:

1. Essence (sattva) - makes something perceptible by the senses; serene, calm, Vishnu.
2. Energy (rajas) - active, fiery, Brahma.
3. Mass (tamas) - inertial, dark, destructive - Shiva.

Then the God Purusa caused a disturbance in the equilibrium, and initiated creation.

The connection from continuum, the prakriti, to the atom, the paranus, was by the aggregation of the gunas into a type of parton called tanmatras. The tanmatras then combined to form the atoms.

There were five types of tanmatras, and they corresponded to the five senses:

1. Vibration - Hearing
2. Momentum - Touch
3. Energy - Sight
4. Viscous Attraction - Taste
5. Cohesive Attraction - Smell

However, they tanmatras themselves were unobservable. Thus they too are confined partons. S.S.S. Sastri comments, "The subtle elements [tanmatras] are not cognisable by us with our limited faculties; their distinctions, thus, not being perceived by us they are non-specific." (Reference: The Sankhyakarika of Isvara Krsna (Univ. of Madras, 1973), pg. 80-81. See also Sankhyakarika 34.)

Conclusion

According to Jung, when we observe more-or-less independent cultures that have developed similar systems of analysis and/or symbolism, we are probably seeing a reflection of a universal tendency of the human mind, an archetype. One of Jung's favorite examples was the mandala, the circular images that are drawn, painted, modelled or danced; often they contain a quarternity or a multiple of four. The physicist Pauli proposed that our basic mathematical intuitions are another example of an archetype.

When the Gaissers realised that ancient Greek atomism had confined partons, as does modern Elementary Particle Physics, I realised that similar analysis can be found in Plato and Sankhya Hinduism (Reference: American Journal of Physics 46, (1978), pg 432.)

Thus, I am proposing that the modern quark model has an archetypal aspect.

BOOTSTRAP THEORIES

Although the quark model has been a success and many physicists believe that quarks actually exist, there are at least two other competing systems of analysis. In this section we discuss one of them, the bootstrap, and will examine the other in the next section.

I shall argue that the bootstrap analysis, just as the quark model, exists in many different contexts, and thus has an archetypal aspect. The discussion has the following sub-sections:

• The Modern Bootstrap
• Buddhist Elements
• Chinese Elements
• Leibniz' Monadology
• Conclusion

The Modern Bootstrap

In the 1920's it was known that the neutron is unstable. If we have a neutron that is not bound inside an atomic nucleus it will decay into a proton and an electron; we now know that in the decay it also emits an antineutrino. This naturally led people to speculate that the neutron was made of a proton plus an electron.

In 1932 Anderson discovered the anti-electron, the positron. This particle is identical to an electron except that it has a positive electric charge instead of a negative charge. A document on antimatter is available here.

This discovery particularly pleased Heisenberg. Now he could view the proton as being made of a neutron and a positron. As he wrote, "The symmetry between the proton and neutron was completely restored. This sounded like Timaeus."

So the neutron is made of a proton, and the proton is made of a neutron. This means that they are made of each other. This is the central idea of the bootstrap: there are no elementary particles, but rather each "particle" is just a reflection of all the other particles. It is called the bootstrap because in this view if I have any one of the particles I can get to all the other particles by lifting the particle by its own bootstraps.

The bootstrap idea is in opposition to the quark model. As Chew remarked, "To a bootstrapper the identification of a seemingly fundamental quark would constitute frustration." (Physics Today 23, (Oct. 1970), 23.)

Instead of trying to classify the elementary particles, this approach concentrates on process, on the various nuclear reactions that can occur. It envisions the universe in terms of an infinite dynamic matrix, the Scattering Matrix, or S-Matrix. And each element of the S-matrix describes a particular nuclear reaction, not a particular nuclear particle.

J.A. Wheeler began work on the S-matrix approach in the 1930's, and was shortly joined by Heisenberg and others.

Chew comments "Carried to its logical extreme, the bootstrap conjecture implies that the existence of consciousness, along with all other aspects of nature, is necessary for self-consistency of the whole." (Science 161, (1968), 762.)

Buddhist Elements

The Buddhists have a five element system of earth, water, air, fire, and ether. Sometimes the ether is omitted, and at other times it is called void. The elements are superficially the same as the Hindu ones, and very similar to the ancient Greek classification of Empedocles. We also note an echo of Plato reserving the fifth regular polyhedron, the dodecahedron, for the fabrication of the universe in this fifth ether/void element.

This concept of void is crucial to Buddhist thought. For example, the Heart Sutra states repeatedly:

"Form is emptiness, emptiness is form.
Likewise the feelings, conceptions, impulses and consciousness."

The concept of void is also closely related to the development of the number zero, which took hold thousands of years ago in Northern India/Southern China. The number zero was adopted by the Arab mathematicians, who finally carried it to Europe. In Europe, however, resistance to its use continued for years. One thing that "carried the day" in Europe was that it is very very difficult to do arithmetic such as long division in Roman numerals, or any other representation without a placeholder like zero.

The following figure of the universe by Sengai (1750 - 1837) represents the void as a zero and seems to echo the Platonic forms discussed above. In "reading" the figure remember to go from right to left.

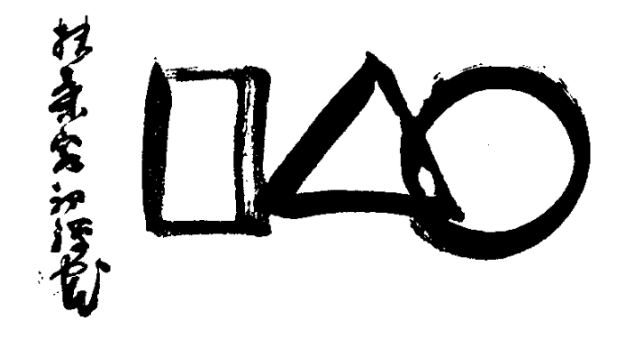
D.T. Suzuki comments on this figure:

"The circle represent the infinite, and the infinite is at the basis of all beings. But the infinite in itself is formless. We humans endowed with senses and intellect demand tangible forms. Hence the triangle. The triangle is the beginning of all forms. Out of it first comes the square. The square is the triangle doubled. This doubling process goes on infinitely." (Sengai the Zen Master pg. 36.)

The Buddhist elements, however, are definitely not atoms. Rather they stand for forces or momentary quanta of energy. We can call them cooperators or cooperating forces. Thus, they are another example of a bootstrap classification. As the Lankavatara Sutra states:

"Long and short and suchlike come to exist mutually conditioned;
not-to-be grows effective by to-be and to-be by not-to-be.
When things are analyzed into atoms, there remains nothing to be discriminated as objects." (D.T. Suzuki trans.)

In fact, the Buddhists provide my personal favorite image of the bootstrap, called Indra's net of pearls:

"In the heaven of Indra, there is said to be a network of pearls, so arranged that if you look at one you see all the others reflected in it. In the same way, each object in the world is not merely itself but involves every other object and in fact is everything else." (Avatamsaka Sutra)

Chinese Elements

In the 4th century B.C. the Chinese were developing classifications that seemed to be a rudimentary form of atomism. However, this was dropped in favor of a system involving the five elements of wood, fire, earth, metal, and water. The origins of these elements goes back at least to the Lu Shih Ch'un Ch'iu of Tsou Yen (c. 350 - 270 B.C.).

The Shu Ching discusses the elements: "The nature of water is to soak and descend; of fire to blaze and ascend; of wood to be crooked and to be straight; of metal to obey and to change; while the virtue of earth is seen in seed-sowing and in gathering." Needham comments: "Chinese thought here characteristically avoided substance and clung to relation." (Science and Civilisation in China, Volume 2, pg. 243.)

In fact the Chinese character for the elements, hsing , also means "go, move" and in ancient times was represented as a cross-roads .

The point is that the Chinese element classification is yet another bootstrap.

Leibniz' Monadology

Leibniz considered the world to be made of fundamental substances called monads. However, as George Gale has realised, the monads are yet another bootstrap:

"Leibniz constantly speaks of the monads as being in `mirroring' relations. But what are the relata of the mirroring relations? Mirrors mirroring other mirrors. Leibniz's monadic kingdom is a pure bootstrap operation." (Journal of the History of Ideas 35, (1974) 339.)

Earlier we made reference to a physicist involved in the modern bootstrap, J.A. Wheeler. He wrote "Not machinery but magic may be the treasure that is waiting. Rather than Newtonian law it may resemble more the logic of relationships that Leibniz envisaged." (in J. Mehra, ed., The Physicist's Conception of Nature.) In fact, the historical argument between Newton and Leibniz about atomism some 300 years ago is mirrored in the modern disagreement between the elementary particle physicists and the bootstrappers.

The fact that Leibniz' monads and the Chinese elements are both bootstraps may not be coincidental or even archetypal. Leibniz' philosophy was strong influenced by Chinese Neo-Confucian thought brought back to Europe by Jesuit missionaries. To the right is the frontispiece of a paper by Leibniz on Chinese philosophy, one of the first such studies carried out in Europe:

Needham comments: "An unexpected vista thus opens before our eyes - the possibility that while the philosophy of fortuitous concourse of atoms, stemming from the society of European city-states, was essential for the construction of modern science in its 19threaucratic society of ancient and medieval China." (Science and Civilisation in China, Volume 2, pg. 339.)

Conclusion

At present the vast majority of high energy physicists are elementary particle physics. One major point of this section is that there is an alternative view, held by physicist and non-physicist alike. Thus I tend to cringe when I see statements like "There is no longer any doubt about the existence of quarks." The quote is from a very popular introductory textbook which I shall refrain from citing.

STRING THEORIES

There is yet another relatively new approach to high energy physics that also relates to theories of gravitation. It is called string theory, and can be traced to 1970. It can be viewed as being consistent with the emphasis on relationship and process that characterises the bootstrap.

Previously it had been somewhat of a cult, but information on it that is accessible to a non-technical audience is now beginning to appear. One nice but now somewhat dated resource is Brian Greene, The Elegant Universe (W.W. Norton, 1999).

On the web I am aware of two excellent sites.

• superstringtheory.com/index.html. A wealth of information, presented in a well designed and well written site. The site is dual track, with both Basic and Advanced discussions of many topics. This site is also the source for the figures that appear below. If you are reading the html version of this document on-line, those figures are animations; the pdf version does not support animations.
• http://online.itp.ucsb.edu/online/plecture/witten/. This page contains an audio presentation and copies of the accompanying overheads for a one hour popular-level talk given by Edward Witten, professor of physics at the Institute for Advanced Study in Princeton, N.J. The talk was given by the Institute for Advanced Physics and the University of California at Santa Barbara in January 1998.

The string theorists hope to solve a long-standing problem. We can classify the world in terms of the interactions that can occur:

1. Strong - responsible for holding the nucleus together.
2. Weak - responsible for radioactive decay.
3. Electromagnetic.
4. Gravitation.

It used to be thought that the magnetic interaction and the electric interaction were separate. They were unified by Faraday and Maxwell into the electromagnetic interaction in the 19th century. Physicists would like to continue unifying these interactions, and some progress has been made on unifying the strong, weak, and electromagnetic forces. However, our best theory of gravitation, Einstein's General Theory of Relativity, continues to stand alone, resisting all attempts at unification.

We can state this situation in a slightly different way. We can describe the strong, weak, and electromagnetic interactions using the Feynman diagrams we saw above. It turns out that this is equivalent to saying that we can describe the interactions using Quantum Mechanics. But no workable Feynman diagrams for the gravitational interaction have been found; there is no unification of Quantum Mechanics and the General Theory of Relativity.

In string theories, as in the bootstrap, there are no particles; there are only strings. The vibrations of the strings is what we normally interpret as the elementary particles. The different modes of vibration correspond to the different particles.

There are two basic types of string theories: those with closed string loops that break into open strings, and those with closed string loops that don't break into open strings

The reason why the elementary objects, electrons, photons, quarks, etc., appear to us to be point-particles instead of vibrating strings is that size of the strings are much too small to be directly seen with current technology.

It turns out that the dimensions of the strings is much greater than the three spatial dimensions and one time dimension we are used to. However, those extra dimensions are "folded up" inside the string, so are unobservable. This is called "compactification."

Currently, the dimensionality of spacetime is believed to be 10 or 11, of which only 4 are normally observable: the three spatial dimensions and the time dimension.

The Feynman diagrams used to describe three of the four elementary interactions have one property which string theories do not: they describe all fundamental interactions as occurring at a single point in space and time, the vertices. One possible reason for the difficulty in unifying these interactions with gravitation is that gravity acts at a distance, not at a point. The figure to the right shows the equivalent of a Feynman diagram in a string theory. String theorists hope that since this reaction is no longer confined to a single point it may be possible to unify all four fundamental interactions.

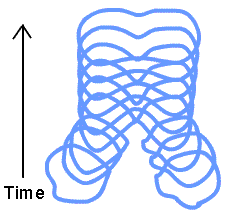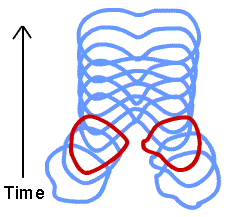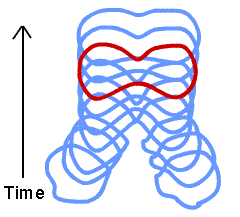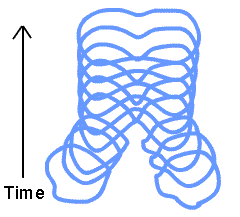
As mentioned above, in its early days string theory was somewhat of a cult. In the past decade or so that situation has been totally reversed. If a young graduate student is interested in questions such as what are the ultimate constituents of the universe, or how does one build a theory of gravity consistent with Quantum Mechanics, that person's chances of getting a job are almost vanishingly small unless they are a string theorist. So string theory now "rules" and other approaches to these fundamental questions are being largely ignored.

This is despite the fact that there really is no such thing as String Theory. What is usually called "String Theory" is actually a program to develop such a theory. That program has been in operation since about 1970. Some critics are now calling the program a failure. One such critic is Lee Smolin of the Perimeter Institutute in Waterloo Ontario: a recent book by him is The Trouble With Physics (Houghton Mifflin, 2007).