2.4: Some Consequences of Fermat’s Principle

Last updated
Save as PDF

Page ID: 57072

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

Homogeneous matter

In homogenous matter, the refractive index is constant and therefore paths of shortest OPL are straight lines. Hence in homogeneous matter rays are straight lines.

Inhomogeneous matter

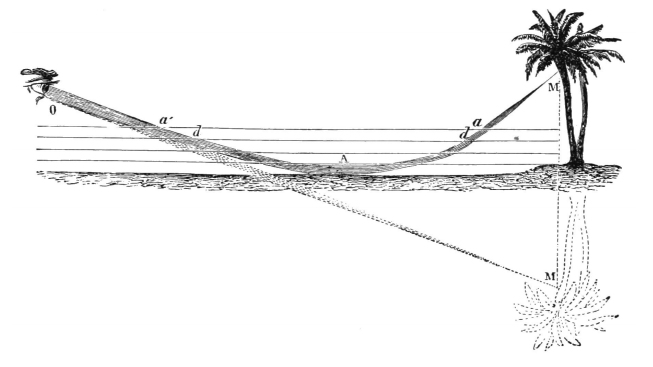
When the refractive index is a function of position such as air with a temperature gradient, the rays bend towards regions of higher refractive index, leading several well-known effects (see Figure \(\PageIndex{1}\) ).

2.2.1.jpg — Figure \(\PageIndex{1}\): Because the temperature close to the ground is higher, the refractive index is lower there. Therefore the rays bend upwards, creating a mirror image of the tree below the ground. (From Popular Science Monthly Volume 5, Public Domain).

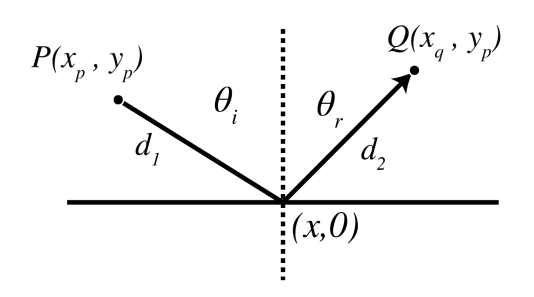
Law of reflection

Consider the mirror shown in Figure \(\PageIndex{2}\) A ray from point P can end up in Q in two ways: by going straight form P to Q or alternatively via the mirror. Both possibilities have different path lengths and hence different travel times and hence both are local minima mentioned at the end of the previous section. We consider here the path by means of reflection by the mirror. Let the x-axis be the intersection of the mirror and the plane through the points P and Q and perpendicular to the mirror. Let the y-axis be normal to the mirror. Let (x_P , y_P ) and (x_Q, y_Q) be the coordinates of P and Q, respectively. If (x, 0) is the point where a ray from P to Q hits the mirror, the travel time of that ray is

\[\dfrac{n}{c}d_{1}(x)+\dfrac{n}{c}d_{2}(x)=\dfrac{n}{c}((x-x_{P})^2+y_{P}^2)^{1/2}+\dfrac{n}{c}((x_{Q}-x)^2+y_{Q}^2)^{1/2}, \nonumber \]

where n is the refractive index of the medium in y > 0. According to Fermat’s Principle, the point (x, 0) should be such that the travel time is minimum , i.e.

\[\dfrac{d}{dx}[d_{1}(x)+d_{2}(x)]=\dfrac{x-x_{P}}{d_{1}(x)}-\dfrac{x_{Q}-x}{d_{2}(x)}=0. \nonumber \]

Hence

\[\sin θ_{i}=\sin θ_{r}, \nonumber \]

\[θ_{r}=θ_{i}. \nonumber \]

where θ_i and θ_r are the angles of incidence and reflection as shown in Figure \(\PageIndex{2}\).

Snell’s law of refraction

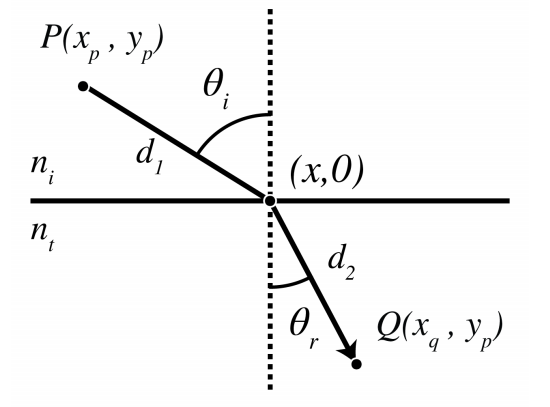
Next we consider refraction at an interface. Let y = 0 be the interface between a medium with refractive index n_i in y > 0 and a medium with refractive index n_t in y < 0. Let (x_P , y_P ) and (x_Q, y_Q) with y_P > 0 and y_Q < 0 be the coordinates of two points P and Q are shown in Figure \(\PageIndex{3}\).

2.2.2.jpg — Figure \(\PageIndex{2}\): Ray from P to Q via the mirror.

What path will a ray follow that goes from P to Q? Since the refractive index is constant in both half spaces, the ray is a straight line in both media. Let (x, 0) be the coordinate of the intersection point of the ray with the interface. Then the travel time is

\[\dfrac{n_{i}}{c}d_{1}(x)+\dfrac{n_{t}}{c}d_{2}(x)=\dfrac{n_{i}}{c}((x-x_{P})^2+y_{P}^2)^{1/2}+\dfrac{n_{t}}{c}((x_{Q}-x)^2+y_{Q}^2)^{1/2}. \nonumber \]

The travel time must be minimum, hence there must hold

\[\dfrac{d}{dx}[n_{i}d_{1}(x)+n_{t}d_{2}(x)]=n_{i}\dfrac{x-x_{P}}{d_{1}(x)}-n_{t}\dfrac{x_{Q}-x}{d_{2}(x)}=0. \nonumber \]

where the travel time has been multiplied by the speed of light in vacuum. Eq. (\(\PageIndex{6}\)) implies

\[n_{i}\sin θ_{i}=n_{t} \sin θ_{t}, \nonumber \]

where \(θ_i\) and \(θ_t\) are the angles between the ray and the normal to the surface in the upper half space and the lower half space, respectively (\(\PageIndex{3}\)).

2.2.3.jpg — Figure \(\PageIndex{3}\): Ray from P to Q, refracted by an interface.

Hence we have derived the law of reflection and Snell’s law from Fermat’s principle. In Chapter 1 the reflection law and Snell’s law have been derived by a different method, namely from the continuity conditions for the electromagnetic field components at the interface.