Skip to main content
Physics LibreTexts

2.5: Perfect Imaging by Conic Sections

  1. Last updated
  2. Save as PDF
  • Page ID
    57073

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

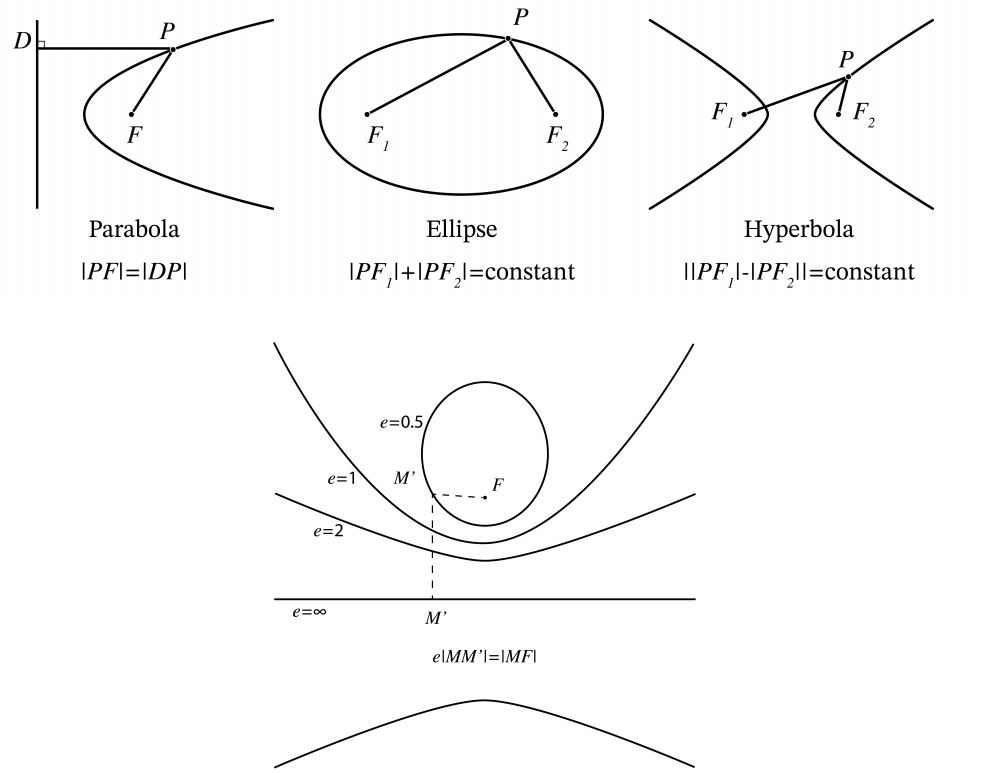
    In this section the conic sections ellipse, hyperbole and parabola are important. In Figure \(\PageIndex{1}\) their definitions are shown as a quick reminder.

    We start with explaining what in geometrical optics is meant by perfect imaging. Let S be a point source. The rays perpendicular to the spherical wave fronts emitted by S radially fan out from S. Due to objects such as lenses etc. the spherical wave fronts are deformed and the direction of the rays start to deviate from the radial propagation direction. When there is a cone of rays coming from point S and all rays in that cone intersect in the same point P, then by Fermat’s principle, all these rays have traversed paths of minimum travel time. In particular, their travel times are equal and therefore they all add up in phase when they arrive in P. Hence at P there is a high light intensity. If there is a cone of rays from point S which all intersect in a point P, point P is called the perfect image of S. By reversing the direction of the rays, S is similarly a perfect image of P. The optical system in which this happens is called stigmatic for the two points S and P.

    2.4.1.jpg
    Figure \(\PageIndex{1}\): Overview of conic sections. The lower figure shows a definition that unifies the three definitions in the figure above by introducing a parameter called the eccentricity e. The point F is the focus and the line e = ∞ is the directrix of the conic sections.
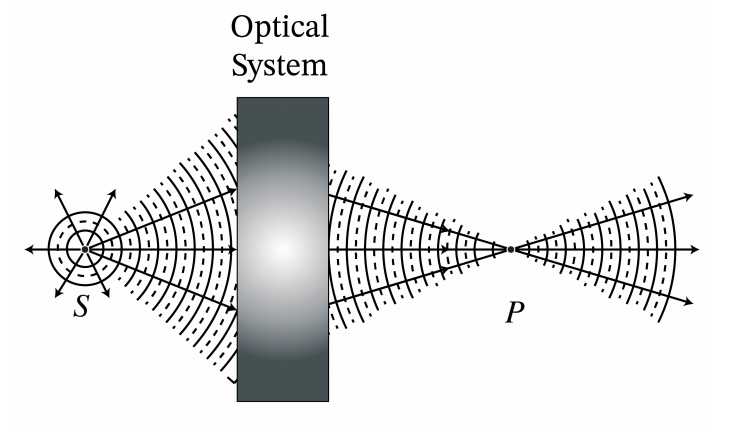
    2.4.2.jpg
    Figure \(\PageIndex{2}\): Perfect imaging: a cone of rays which diverge from S and all intersect in point P. The rays continue after P.

    Remark. The concept of a perfect image point exists only in geometrical optics. In reality finite apertures of lenses and other imaging systems cause diffraction due to which image points are never perfect but blurred.

    We summarise the main examples of stigmatic systems.

    1. Perfect focusing and imaging by refraction. A parallel bundle of rays propagating in a medium with refractive index n2 can be focused into a point F in a medium n1. If n2 > n1, the interface between the media should be a hyperbole with focus F, whereas if n2 < n1 the interface should be an ellipse with focus F (see Figs. \(\PageIndex{3}\) ) and \(\PageIndex{4}\). By reversing the rays we obtain perfect collimation. Therefore, a point S in air can be perfectly imaged onto a point F in air by inserting a piece of glass in between them with hyperbolic surfaces as shown in Figure \(\PageIndex{4}\).
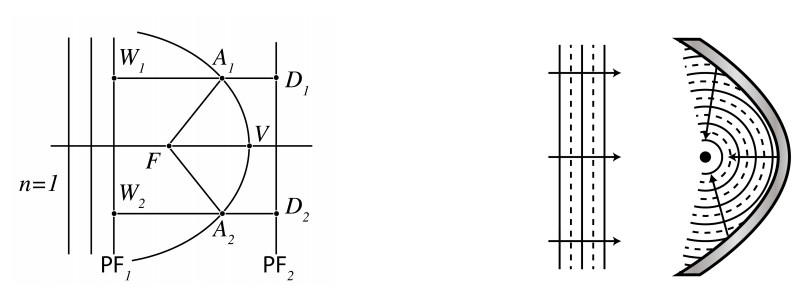
    2. Perfect focusing of parallel rays by a mirror. A bundle of parallel rays in air can be focused into a point F by a mirror of parabolic shape with F as focus (see Figure \(\PageIndex{5}\). By reversing the arrows, we get (within geometrical optics) a perfectly parallel beam. Parabolic mirrors are used everywhere, from automobile headlights to radio telescopes.

    The remainder of this section can be skipped since the following demonstrations that the ellipse, hyperbole and parabole are stigmatic for certain points are not essential for the sequel. First suppose that there are two media with refractive indices n1 > n2 and that point S is at infinity in the medium with refractive index n2. We will construct a surface (interface) between the two media such that all rays from S are focused into the same point F (see Figure \(\PageIndex{3}\)a). Because S is at very large distance, the rays entering from the right are parallel. Since all parallel rays have travelled the same distance when they hit the surface DD' perpendicular to the rays, all parallel rays have the same phase at their intersection points with the plane DD' . If point A is on the interface sought for, the travel time for a ray from D to F via A must be minimum and hence must be the same for all points A. Hence

    \[\dfrac{n_{2}}{c}|DA| +\dfrac{n_{1}}{c}|AF|=constant, \nonumber \]

    where “constant” means the same value for all rays, hence for all points A on the interface. By moving the plane DD' parallel to itself, we can achieve that for this new plane DD' we get:

    \[e|DA|+|AF|=0, \nonumber \]

    where e = n2/n1 < 1. Hence the set of points A defines an ellipsoid.

    In contrast, when n2 < n1, as shown at the right of Figure \(\PageIndex{3}\), then e < 1 and we have an ellipsoid with F as one of its focal points.

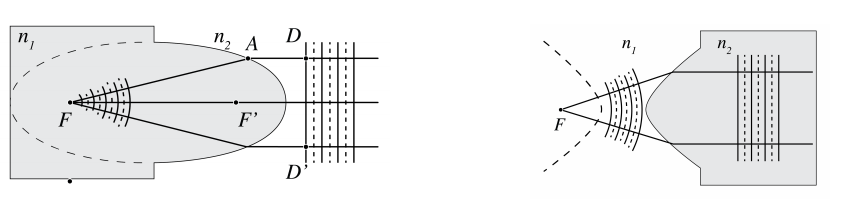
    2.4.3.png
    Figure \(\PageIndex{3}\): (a) Ellipsoid (n2 < n1) and (b) hyperboloid to perfectly focus a parallel beam incident from the medium with refractive index n2 into a point in a medium with refractive index n1.
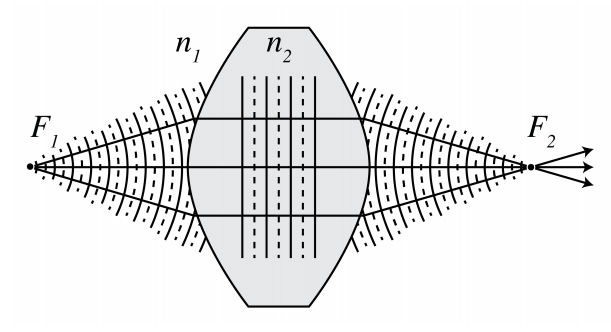
    2.4.4.jpg
    Figure \(\PageIndex{4}\): Lens with hyperboloid surfaces for perfect imaging of a pair of points.

    The direction of the rays in Figure \(\PageIndex{3}\) can obviously also be reversed in which case the rays from point F are all perfectly collimated (i.e. parallel). If medium 2 consists of glass and medium 1 of air, we conclude that by joining two hyperboloids as shown in Figure \(\PageIndex{4}\), point S in air is perfectly imaged to point P, also in air.

    Next we consider perfect focusing of parallel rays by a mirror. Let there be a parallel bundle of rays in air (n = 1) and suppose we want to focus all rays in point F. We draw a plane Σ1 perpendicular to the rays as shown in Figure \(\PageIndex{5}\). The rays that hit Σ1 have traversed the same optical path length. We draw a second surface Σ2 parallel to Σ1. Consider rays hitting the mirror in A1 and A2. The OPL from Wj via Aj to F must be the same for all rays:

    \[OPL=|W_{1}A_{1}|+| A_{1} F|= |W_{2}A_{2}|+| A_{2} F| . \nonumber \]

    Since Σ2 is parallel to Σ1:

    \[|W_{1}A_{1}|+| A_{1} D_{1}|= |W_{2}A_{2}|+| A_{2}D_{2}| \nonumber \]

    Hence (\(\PageIndex{3}\)) will be satisfied for points A for which |AF| = |AD|, i.e. for which the distance to F is the same as to Σ2. This is a paraboloid with F as focus and Σ2 as directrix.

    2.4.5.jpg
    Figure \(\PageIndex{5}\): A paraboloid mirror.

    Remark.

    Although we found that conic surfaces give perfect imaging for a certain pair of points, other points do not have perfect images in the sense that for a certain cone of rays, all rays are refracted (or reflected) to the same point.

    External sources in recommended order

    This page titled 2.5: Perfect Imaging by Conic Sections is shared under a CC BY-NC-SA 4.0 license and was authored, remixed, and/or curated by Sander Konijnenberg, Aurèle J.L. Adam, & H. Paul Urbach (TU Delft Open) via source content that was edited to the style and standards of the LibreTexts platform; a detailed edit history is available upon request.