1.3: Refraction at a Plane Surface
( \newcommand{\kernel}{\mathrm{null}\,}\)
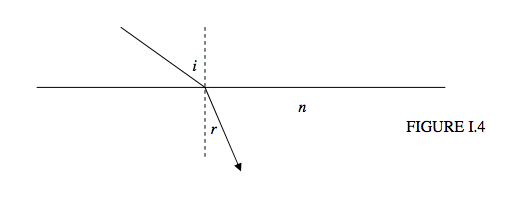
When a ray of light enters a denser medium it is refracted towards the normal in such a manner than the ratio of the sine of the angle of incidence to the sine of the angle of refraction is constant, this constant being called the refractive index n.
This is all right as far as it goes, but we may be able to do better.
- Remember the curmudgeonly professor who will give you only half marks unless you also say that the incident ray, the refracted ray and the normal are coplanar.
- The equation
sinisinr=n,
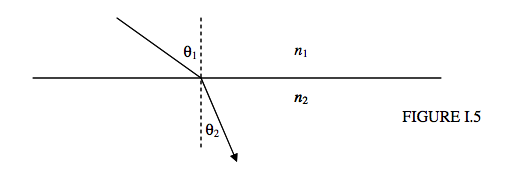
where n is the refractive index of the medium, is all right as long as the light enters the medium from a vacuum. The refractive index of air is very little different from unity. Details on the refractive index of air may be found in Section 7.1 of Stellar Atmospheres and Section 11.3.3 of Celestial Mechanics. If light is moving from one medium to another, the law of refraction takes the form
n1sinθ1=n2sinθ2.
iii. The statement of Snell’s law as given above implies, if taken literally, that there is a one-to-one relation between refractive index and density. There must be a formula relating refractive index and density. If I tell you the density, you should be able to tell me the refractive index. And if I tell you the refractive index, you should be able to tell me the density. If you arrange substances in order of increasing density, this will also be their order of increasing refractive index.
Not Quite True
This is not quite true, and, if you spend a little while looking up densities and refractive indices of substances in, for example, the CRC Handbook of Physics and Chemistry, you will find many examples of less dense substances having a higher refractive index than more dense substances. It is true in a general sense usually that denser substances have higher indices, but there is no one-to-one correspondence.
In fact light is bent towards the normal in a “denser” medium as a result of its slower speed in that medium, and indeed the speed v of light in a medium of refractive index n is given by
n=c/v,
where c is the speed of light in vacuo. Now the speed of light in a medium is a function of the electrical permittivity ϵ and the magnetic permeability μ:
v=1/√ϵμ.
The permeability of most nonferromagnetic media is very little different from that of a vacuum, so the refractive index of a medium is given approximately by
n≈√ϵϵ0
Thus there is a much closer correlation between refractive index and relative permittivity (dielectric constant) than between refractive index and density. Note, however, that this is only an approximate relation. In the detailed theory there is a small dependence of the speed of light and hence refractive index on the frequency (hence wavelength) of the light. Thus the refractive index is greater for violet light than for red light (violet light is refracted more violently). The splitting up of white light into its constituent colours by refraction is called dispersion.
Here is a ray of light travelling from one medium to another:
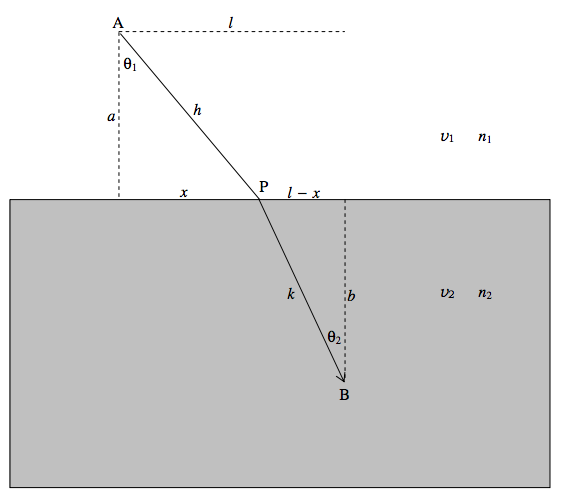
It moves faster in the upper medium than in the lower medium.
Time taken to get from A to B:
t=√a2+x2v1+√b2+(1−x)2v2.
That is:
ct=n1√a2+x2+n2√b2+(l−x)2.
Here is the time taken as a function of the position of P, calculated for n2/n1=1.5.
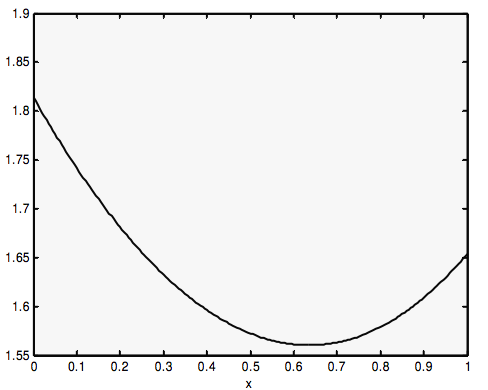
As you see, it goes through a minimum. You can find where it is by differentiating Equation ???:
cdtdx=n1x√a2+x2−n2(l−x)√b2+(l−x)2=n1sinθ1−n2sinθ2,
This is zero when n1sinθ1−n2sinθ2=0. Thus Snell’s law is such that the path actually taken is the path that takes the shortest time. Trivial, or profound?
Huygens’ Construction
Here is a wavefront moving upwards. “Light “rays” are normals to the wavefront.

Huygens’ construction is a way of prediction what will happen next. It says that you can imagine every point on the wavefront to be a source that generates a little wavelet. Then, after a little time the wavelets look like this - and the new wavefront is the common tangent to all the wavelets.

This may sound trivial at first, although much has been written about it - i.e. whether it represents reality, or is merely a convenient construction. And, if real, what happens to the wavelets in the backwards direction? We’ll not pursue that here, but we can use the Huygens construction as an interesting way to think about Snell’s law.
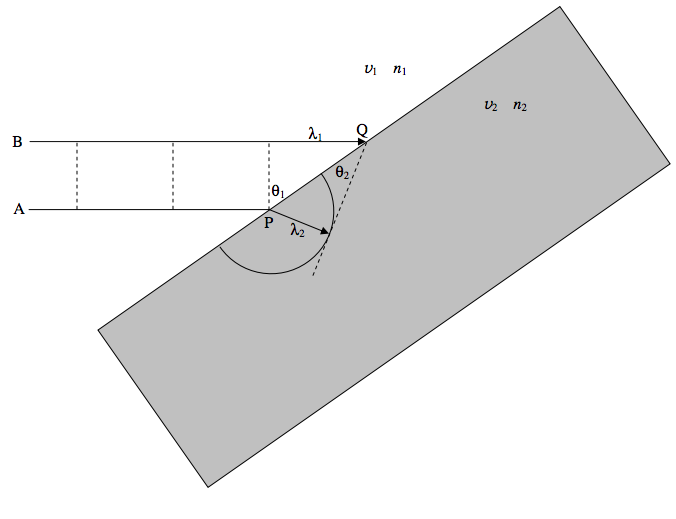
A beam of light of wavelength λ1 is approaching a glass block from the left at speed v1. The dashed lines represent the wavefronts. Ray A reaches the block first, at P. A wavelet is generated at P, moving with speed v2. The drawing is made for the instant when ray B reaches the point Q. The new wavefront is the tangent from Q to the little wavelet that started at P. The geometry will show that λ1λ2=v1v2=n2n1 and therefore sinθ1=n2sinθ2.
Example 1.3.1: Refraction through a glass block
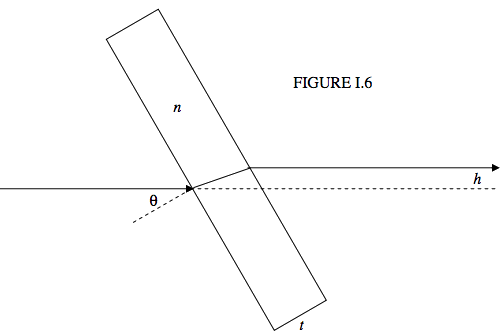
Figure I.6 shows a ray of light passing through a rectangular glass block of thickness t and refractive index n (taken to be 1.5 in the drawing). The normal to the surface of the block makes an angle θ with the incoming ray. It is a matter of simple geometry (do it!) to show that the lateral displacement h of the ray is given by
h=t(sinθ−cosθtanϕ),
where ϕ is the angle of refraction, given by sinθ=nsinϕ. In terms of θ,n and t, this is
h=tsinθ(1−cosθ√n2−sin2θ).
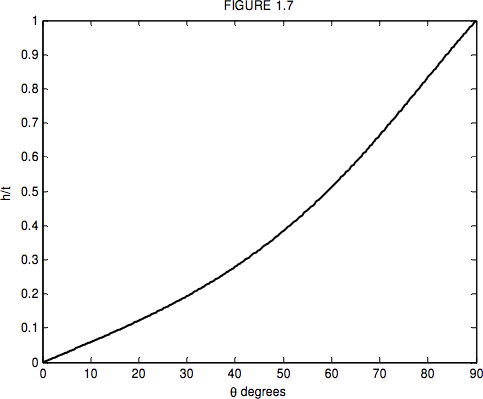
Figure I.7 is drawn for n=1.5.
One might imagine making use of this to measure the distance between two points close together. For example suppose that you have a photograph of some stars on an old photographic plate, and it includes a close pair of stars, and you want to measure the distance between the two star images. (Today the photograph would be on a CCD detector, and the distance between the two images would be recorded electronically, which is why I specify an old photographic plate.) You look at the photograph through a microscope and see one of the stars bisected by a crosshair in the microscope eyepiece. But you have a glass plate in front of the photograph, and you tilt the plate in order to displace the images so that the images move and the second star is now bisected by the crosshair. From the large angle through which you tilt the plate you can work out the tiny distance between the two images. You’ll want to use monochromatic light, and you’d need to know the refractive index at that wavelength.
How will you measure the angle through which the plate has turned? Well, you could shine a laser beam off it; the reflected light will move at twice the speed of the plate, and you could let it illuminate a sheet of graph paper several feet away. Thus the tiny distance between the images will correspond to a large distance on the graph paper. There may be one or two other practical details that you’d want to think about. For example, how thick would you want the glass plate to be? A thin microscope slide, maybe, or something much thicker than that? Would it be better to work at angles θ less than about 40º where the slope of Figure I.7 is small, or at angles greater than 50º where the slope is larger?
You might also wish to move a laser beam sidewise through a small and controlled amount. You could put a glass block on a turntable which could be rotated through a tiny measurable angle and thus move the laser beam laterally and accurately through a very tiny amount.
Let’s continue with the glass block.
Example 1.3.2: Refraction through a moving glass block
Show that, if the glass block were to be rotated counterclockwise with angular speed ω, the laser beam would move upwards at a speed
˙h=t[cosθ−n2−2n2sin2θ+sin4θ(n2−sin2θ)3/2]ω
If we write sin2θ as 1−cos2θ, we’ll be able to express this entirely in terms of cosθ. And if, for illustrative purposes, I take n=1.5, the equation becomes
˙htω=c+1.25−2.5c2−c4(1.25+c2)3/2,
where c=cosθ. For ease in computation, I’ll set C=c2. Equation ??? then becomes
˙htω=c+1.25−C(2.5+C)(1.25+C)3/2.
This is easy to compute, and the result is shown in the graph below.
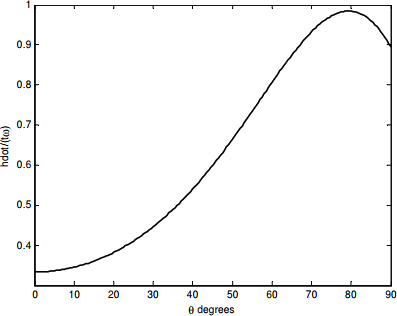
We see, perhaps to our surprise, that ˙h & goes through a maximum at about θ = 79º. To obtain Equation ???, we had to differentiate Equation ???. Now, to find out where ˙h goes through a maximum, we are going to have to differentiate again, although mercifully we can differentiate Equation ??? with respect to C rather than to θ. If we do this, and then set the derivative to zero, we find, after some simplification,
12C1/2=5+1.25C+0.5C2(1.25+C)5/2
If we square this and collect powers of C, we arrive at a quartic equation in C:
625−17980C−6240C2−2176C3+256C4=0.
where C=c2=cos2θ.
The solution to this equation is C=0.0343465490, corresponding to
θ = 79º.319 731 1


