4.4: Barrier Penetration
( \newcommand{\kernel}{\mathrm{null}\,}\)
In order to understand quantum mechanical tunnelling in fission it makes sense to look at the simplest fission process: the emission of a He nucleus, so called α radiation (Figure 4.4.1).
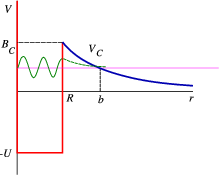
Suppose there exists an α particle inside a nucleus at an (unbound) energy >0. Since it isn’t bound, why doesn’t it decay immediately? This must be tunnelling. In Figure 4.4.1) we have once again shown the nuclear binding potential as a square well (red curve), but we have included the Coulomb tail (blue curve),
VCoulomb(r)=(Z−2)2e24πϵ0r.
The height of the barrier is exactly the coulomb potential at the boundary, which is the nuclear radius, RC=1.2A1.3 fm, and thus BC=2.4(Z−2)A−1/3. The decay probability across a barrier can be given by the simple integral expression P=e−2γ, with
γ=(2μα)1/2ℏ∫bRC[V(r)−Eα]1/2dr=(2μα)1/2ℏ∫bRC[2(Z−2)e24πϵ0r−Eα]1/2dr=2(Z−2)e22πϵ0ℏv[arccos(Eα/BC)−(Eα/BC)(1−Eα/BC)],
where v is the velocity associated with Eα. In the limit that BC≫Eα we find
P=exp[−2(Z−2)e22ϵ0ℏv].
This shows how sensitive the probability is to Z and v!


