4.2: Decoherence
( \newcommand{\kernel}{\mathrm{null}\,}\)
The density operator allows us to consider the phenomenon of decoherence. Consider the pure state |+⟩. In matrix notation with respect to the basis {|+⟩,|−⟩}, this can be written as
ρ=(1000)
The trace is 1, and one of the eigenvalues is 1, as required for a pure state. We can also write the density operator in the basis {|0⟩,|1⟩}:
ρ=|+⟩⟨+|=1√2(11)×1√2(1,1)=12(1111).
Notice how the outer product (as opposed to the inner product) of two vectors creates a matrix representation of the corresponding projection operator.
Let the time evolution of |+⟩ be given by
|+⟩=|0⟩+|1⟩√2→|0⟩+eiωt|1⟩√2.
The corresponding density operator becomes
ρ(t)=12(1eiωte−iωt1).
The “population” in the state |+⟩ is given by the expectation value
⟨+|ρ(t)|+⟩=12+12cos(ωt).This oscillation is due to the off-diagonal elements of ρ(t), and it is called the coherence of the system (see Fig. 2).
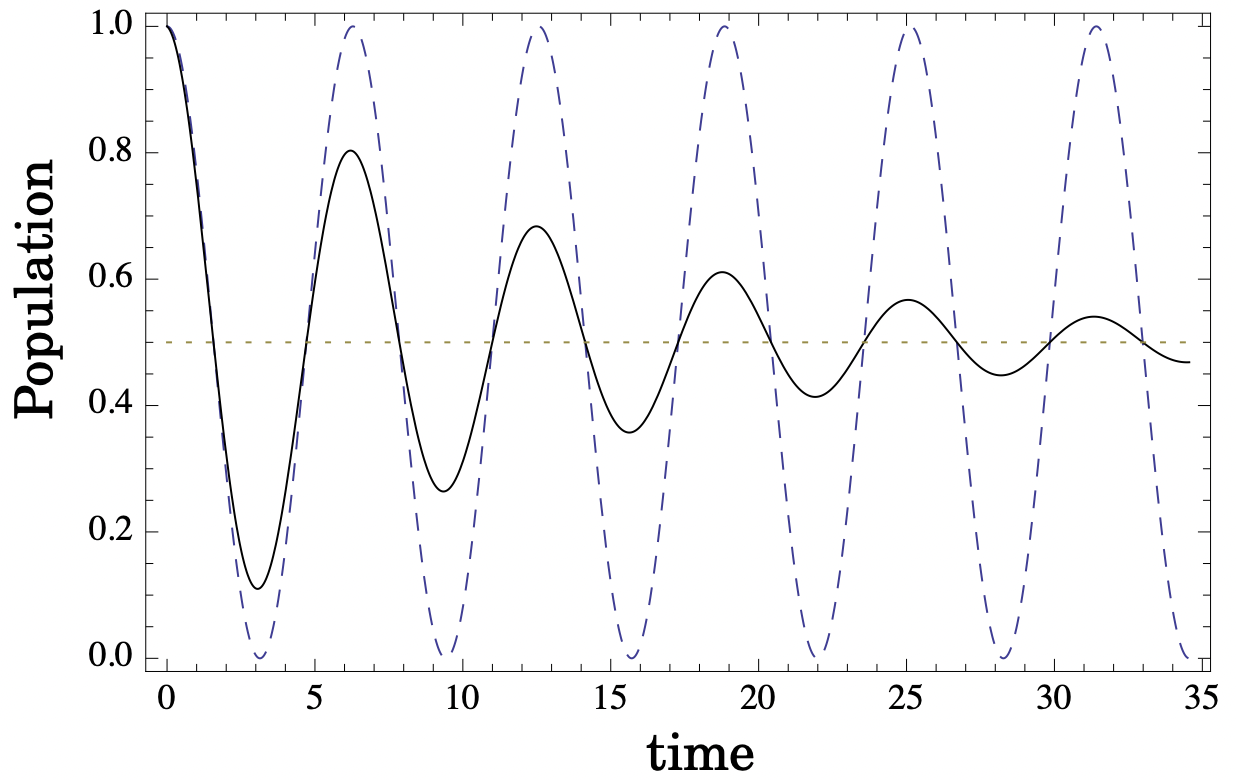
The state is pure at any time t. In real physical systems the coherence often decays exponentially at a rate γ, and the density matrix can be written as
ρ(t)=12(1eiωt−γte−iωt−γt1).
The population in the state |+⟩ decays accordingly as
⟨+|ρ(t)|+⟩=12+e−γtcos(ωt)2.
This is called decoherence of the system, and the value of γ depends on the physical mechanism that leads to the decoherence.
The decoherence described above is just one particular type, and is called dephasing. Another important decoherence mechanism is relaxation to the ground state. If the state |1⟩ has a larger energy than |0⟩ there may be processes such as spontaneous emission that drive the system to the ground state. Combining these two decay processes, we can write the density operator as
ρ(t)=12(2−e−γ1teiωt−γ2te−iωt−γ2te−γ1t).
The study of decoherence is currently one of the most important research areas in quantum physics.


