5.4: Coherence

In the discussion so far we have only considered monochromatic light, which means that the spectrum of the light consists of only one frequency. Although light from a laser often has a very narrow band of frequencies and therefore can be considered to be monochromatic, purely monochromatic light does not exist. All light consists of multiple frequencies and therefore is polychromatic. Classical light sources such as incandescent lamps and also LEDs have relatively broad frequency bands. The question then arises how differently polychromatic light behaves compared to the idealised case of monochromatic light. To answer this question, we must study the topic of coherence. One distinguishes between two extremes: fully coherent and fully incoherent light, while the degree of coherence of practical light is somewhere in between. Generally speaking, the broader the frequency band of the source, the more incoherent the light is. It is a very important observation that no light is actually completely coherent or completely incoherent. All light is partially coherent, but some light is more coherent than others.

An intuitive way to think about these concepts is in terms of the ability to form interference fringes. For example, with laser light, which usually is almost monochromatic and hence coherent, one can form an interference pattern with clear maxima and minima in intensities (so-called fringes) using a double slit, while with sunlight (which is incoherent) this is much more difficult. Every frequency in the spectrum of sunlight gives its own interference pattern with its own frequency dependent fringe pattern. These fringe patterns wash out due to superposition and the total intensity therefore shows little fringe contrast, i.e. the coherence is less. However, it is not impossible to create interference fringes with natural light. The trick is to let the two slits be so close together (of the order of \(0.02 \mathrm{~mm}\) ) that the difference in distances from the slits to the sun is so small for the fields in the slits are sufficiently coherent to interfere. To understand the effect of polychromatic light, it is essential to understand that the degree to which the fields in two points are coherent, i.e. the ability to form fringes, is determined by the difference in distances between these points and the source. The distance itself to the source is not relevant. In the next sections we study these issues more quantitatively.

5.3.1 Coherence of Light Sources

In a conventional light source such as a gas discharge lamp, photons are generated by electronic transitions in the atoms of the gas. These transitions have a duration of the order of \(10^{-8}\) to \(10^{-9} \mathrm{~s}\). Because the emitted wave trains are finite, the emitted light does not have a single frequency; instead, there is a band of frequencies around a centre frequency. This spread of frequencies is called the natural linewidth. Random thermal motions of the molecules cause further broadening due to the Doppler effect. In addition, the atoms undergo collisions that interrupt the wave trains and therefore further broaden the frequency spectrum.

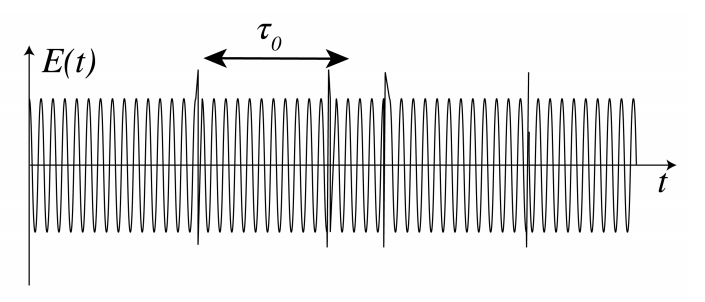
We first consider a single emitting atom. When collisions are the dominant broadening effect and these collisions are sufficiently brief, so that any radiation emitted during the collision can be ignored, an accurate model for the emitted wave is a steady monochromatic wave train at frequency \(\bar{\omega}\) at the centre of the frequency band, interrupted by random phase jumps each time that a collision occurs. The discontinuities in the phase due to the collisions cause a spread of frequencies around the centre frequency. An example is shown in Figure \(\PageIndex{1}\). The average time \(\tau_{0}\) between the collisions is typically less than 10 ns which implies that on average between two collisions roughly 150,000 harmonic oscillations occur. The coherence time \(\Delta \tau_{c}\) is defined as the maximum time interval over which the phase of the electric field can be predicted. In the case of collisions-dominated emission by a single atom, the coherence time is equal to the average time between subsequent collisions: \(\Delta \tau_{c}=\tau_{0}\).

To understand coherence and incoherence, it is very helpful to use this model for the emission by a single atom as harmonic wave trains of thousands of periods interrupted by random phase jumps. The coherence time and the width \(\Delta \omega\) of the frequency line are related as

Figure \(\PageIndex{1}\): The electric field amplitude of the harmonic wave train radiated by a single atom at the centre frequency \(\bar{\omega}\). The vertical lines are collisions separated by periods of free flight with mean duration \(\tau_{0}\). The quantity \(\bar{\omega} \tau_{0}\), which is the number of periods in a typical wave train, is chosen unrealistically small (namely 60 , whereas a realistic value would be \(10^{5}\) ), to show the random phase changes.

\[\Delta \tau_{c}=\frac{2 \pi}{\Delta \omega} \nonumber \]

The coherence length is defined by \[\Delta \ell_{c}=c \Delta \tau_{c} . \nonumber \]

Since \(\lambda \omega=2 \pi c\), we have \[\frac{\Delta \lambda}{\bar{\lambda}}=\frac{\Delta \omega}{\bar{\omega}}, \nonumber \] where \(\lambda\) and \(\bar{\omega}\) are the wavelength and the frequency at the centre of the line. Hence, \[\Delta \ell_{c}=c \frac{2 \pi}{\Delta \omega}=2 \pi \frac{c}{\bar{\omega}} \frac{\bar{\omega}}{\Delta \omega}=\frac{\bar{\lambda}^{2}}{\Delta \lambda} \nonumber \]

The coherence length and coherence time of a number of sources are listed in Table \(\PageIndex{1}\).

Table \(\PageIndex{1}\): Coherence time and length of several sources

Source	Mean wavelength	Linewidth	Coherence Length	Coherence Time
	\(\bar{\lambda}\)	\(\Delta \lambda\)	\(\bar{\lambda}^{2} / \Delta \lambda\)	\(\frac{\bar{\lambda}}{\Delta \lambda} \frac{\bar{\lambda}}{c}\)
Mid-IR (3-5 \(\mu \mathrm{m}\) )	\(4.0 \mu \mathrm{m}\)	\(2.0 \mu \mathrm{m}\)	\(8.0 \mu \mathrm{m}\)	\(2.66 \times 10^{-14} \mathrm{~s}\)
White light	\(550 \mathrm{~nm}\)	\(\approx 300 \mathrm{~nm}\)	\(\approx 900 \mathrm{~nm}\)	\(\approx 3.0 \times 10^{-14} \mathrm{~s} .\)
Mercury arc	\(546.1 \mathrm{~nm}\)	\(\approx 1.0 \mathrm{~nm}\)	\(\approx 0.3 \mathrm{~mm}\)	\(\approx 1.0 \times 10^{-12} \mathrm{~s} .\)
Kr \(^{86}\) discharge lamp	\(605.6 \mathrm{~nm}\)	\(1.2 \times 10^{-3} \mathrm{~nm}\)	\(0.3 \mathrm{~m}\)	\(1.0 \times 10^{-9} \mathrm{~s} .\)
Stabilised He-Ne laser	\(632.8 \mathrm{~nm}\)	\(\approx 10^{-6} \mathrm{~nm}\)	\(400 \mathrm{~m}\)	\(1.33 \times 10^{-6}\) s.

5.3.2 Polychromatic Light

When dealing with coherence one has to consider fields that consist of a range of different frequencies. Let \(\mathcal{U}(\mathbf{r}, t)\) be the real-valued physical field component. It is always possible to write \(\mathcal{U}(\mathbf{r}, t)\) as an integral over time-harmonic components: \[\mathcal{U}(\mathbf{r}, t)=\operatorname{Re} \int_{0}^{\infty} A_{\omega}(\mathbf{r}) e^{-i \omega t} \mathrm{~d} \omega, \nonumber \] where \(A_{\omega}(r)\) is the complex amplitude of the time-harmonic field with frequency \(\omega\). When there is only a certain frequency band that contributes, then \(A_{\omega}=0\) for \(\omega\) outside this band. We define the complex time-dependent field \(U(\mathbf{r}, t)\) by \[U(\mathbf{r}, t)=\int_{0}^{\infty} A_{\omega}(\mathbf{r}) e^{-i \omega t} \mathrm{~d} \omega . \nonumber \]

Then \[\mathcal{U}(\mathbf{r}, t)=\operatorname{Re} U(\mathbf{r}, t) \nonumber \]

Remark: The complex field \(U(\mathbf{r}, t)\) contains now the time dependence in contrast to the notation used for a time-harmonic (i.e. single frequency) field introduced in Chapter 2, where the time-dependent \(e^{-i \omega t}\) was a separate factor.

Quasi-monochromatic field. If the width \(\Delta \omega\) of the frequency band is very narrow, we speak of quasi-monochromatic flight. In the propagation of quasi-monochromatic fields, we use the formula for time-harmonic fields at the centre frequency \(\bar{\omega}\). The quasi-monochromatic assumption simplifies the computations considerably. Nevertheless, most of the treatment that follows is more general and does not assume that the field is quasi-monochromatic.

We now compute the intensity of polychromatic light. The instantaneous energy flux is (as for monochromatic light) proportional to the square of the instantaneous real field: \(\mathcal{U}(\mathbf{r}, t)^{2}\). We average the instantaneous intensity over the integration time \(T\) of common detectors which, as stated before, is very long compared to the period at the centre frequency \(2 \pi / \bar{\omega}\) of the field (at least \(10^{5}\) times the period of the light). Using definition (5.2.6) and \[\mathcal{U}(\mathbf{r}, t)=\operatorname{Re} U(\mathbf{r}, t)=\left(U(\mathbf{r}, t)+U(\mathbf{r}, t)^{*}\right) / 2, \nonumber \] we get \[\begin{aligned} \left\langle\mathcal{U}(\mathbf{r}, t)^{2}\right\rangle &=\frac{1}{4}\left\langle\left(U(\mathbf{r}, t)+U(\mathbf{r}, t)^{*}\right)\left(U(\mathbf{r}, t)+U(\mathbf{r}, t)^{*}\right)\right\rangle \\ &=\frac{1}{4}\left\{\left\langle U(\mathbf{r}, t)^{2}\right\rangle+\left\langle\left(U(\mathbf{r}, t)^{*}\right)^{2}\right\rangle+2\left\langle U(\mathbf{r}, t)^{*} U(\mathbf{r}, t)\right\rangle\right\} \\ &=\frac{1}{2}\left\langle U(\mathbf{r}, t)^{*} U(\mathbf{r}, t)\right\rangle \\ &=\frac{1}{2}\left\langle|U(\mathbf{r}, t)|^{2}\right\rangle . \end{aligned} \nonumber \] where the averages of \(U(\mathbf{r}, t)^{2}\) and \(\left(U(\mathbf{r}, t)^{*}\right)^{2}\) are zero because they are fast-oscillating functions of time. In contrast, \(|U(\mathbf{r}, t)|^{2}=U(\mathbf{r}, t)^{*} U(\mathbf{r}, t)\) has a DC-component which does not average to zero.

Remark: In contrast to the time-harmonic case, the long time average of polychromatic light depends on the time \(t\) at which the average is taken. However, we assume in this chapter that the fields are omitted by sources that are stationary. The property of stationarity implies that the average over the time interval of long length \(T\) does not depend on the time that the average is taken. Many light sources, in particular conventional lasers, are stationary. (However, a laser source which emits short high-power pulses cannot be considered as a stationary source). We furthermore assume that the fields are ergodic, which means that taking the time-average over a long time interval amounts to the same as taking the average over the ensemble of possible fields. It can be shown that this property implies that the limit \(T \rightarrow \infty\) in (5.2.6) indeed exists.

We use for the intensity again the expression without the factor \(1 / 2\) in front, i.e. \[I(\mathbf{r})=\left\langle|U(\mathbf{r}, t)|^{2}\right\rangle . \nonumber \] The time-averaged intensity has hereby been expressed in terms of the time-average of the squared modulus of the complex field.