2.10: Wave-Packets
( \newcommand{\kernel}{\mathrm{null}\,}\)
The previous discussion suggests that the wavefunction of a massive particle of momentum p and energy E, moving in the positive x-direction, can be written ψ(x,t)=ˉψei(kx−ωt), where k=p/ℏ>0 and ω=E/ℏ>0. Here, ω and k are linked via the dispersion relation ([e2.38]). Expression ([e2.41]) represents a plane-wave whose maxima and minima propagate in the positive x-direction with the phase-velocity vp=ω/k. As we have seen, this phase-velocity is only half of the classical velocity of a massive particle.
From before, the most reasonable physical interpretation of the wavefunction is that |ψ(x,t)|2 is proportional to the probability density of finding the particle at position x at time t. However, the modulus squared of the wavefunction ([e2.41]) is |ˉψ|2, which depends on neither x nor t. In other words, this wavefunction represents a particle that is equally likely to be found anywhere on the x-axis at all times. Hence, the fact that the maxima and minima of the wavefunction propagate at a phase-velocity that does not correspond to the classical particle velocity does not have any real physical consequences.
How can we write the wavefunction of a particle that is localized in x: that is, a particle that is more likely to be found at some positions on the x-axis than at others? It turns out that we can achieve this goal by forming a linear combination of plane-waves of different wavenumbers: in other words, ψ(x,t)=∫∞−∞ˉψ(k)ei(kx−ωt)dk. Here, ˉψ(k) represents the complex amplitude of plane-waves of wavenumber k in this combination. In writing the previous expression, we are relying on the assumption that particle waves are superposable: that is, that it is always possible to add two valid wave solutions to form a third valid wave solution. The ultimate justification for this assumption is that particle waves satisfy a differential wave equation that is linear in ψ. As we shall see, in Section 1.15, this is indeed the case. Incidentally, a plane-wave that varies as exp[i(kx−ωt)] and has a negative k (but positive ω) propagates in the negative x-direction at the phase-velocity ω/|k|. Hence, the superposition ([e2.42]) includes both forward and backward propagating waves.
There is a useful mathematical theorem, known as Fourier’s theorem , which states that if f(x)=1√2π∫∞−∞ˉf(k)eikxdk, then ˉf(k)=1√2π∫∞−∞f(x)e−ikxdx. Here, ˉf(k) is known as the Fourier transform of the function f(x). We can use Fourier’s theorem to find the k-space function ˉψ(k) that generates any given x-space wavefunction ψ(x) at a given time.
For instance, suppose that at t=0 the wavefunction of our particle takes the form ψ(x,0)∝exp[ik0x−(x−x0)24(Δx)2]. Thus, the initial probability density of the particle is written |ψ(x,0)|2∝exp[−(x−x0)22(Δx)2]. This particular probability distribution is called a Gaussian distribution, and is plotted in Figure [f4]. It can be seen that a measurement of the particle’s position is most likely to yield the value x0, and very unlikely to yield a value which differs from x0 by more than 3Δx. Thus, Equation ([e2.45]) is the wavefunction of a particle that is initially localized around x=x0 in some region whose width is of order Δx. This type of wavefunction is known as a wave-packet.
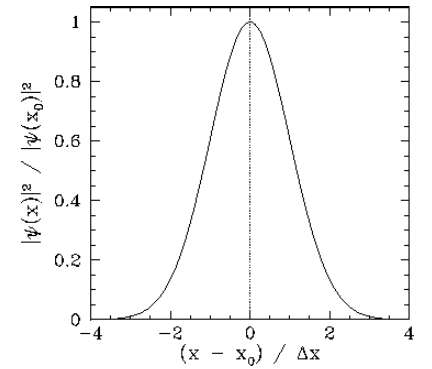
Figure 7: A Gaussian probability distribution in ![]() -space.
-space.
According to Equation ([e2.42]), ψ(x,0)=∫∞−∞ˉψ(k)eikxdk. Hence, we can employ Fourier’s theorem to invert this expression to give ˉψ(k)∝∫∞−∞ψ(x,0)e−ikxdx. Making use of Equation ([e2.45]), we obtain ˉψ(k)∝e−i(k−k0)x0∫∞−∞exp[−i(k−k0)(x−x0)−(x−x0)24(Δx)2]dx. Changing the variable of integration to y=(x−x0)/(2Δx), this reduces to ˉψ(k)∝e−ikx0∫∞−∞exp(−iβy−y2)dy, where β=2(k−k0)Δx. The previous equation can be rearranged to give ˉψ(k)∝e−ikx0−β2/4∫∞−∞e−(y−y0)2dy, where y0=−iβ/2. The integral now just reduces to a number, as can easily be seen by making the change of variable z=y−y0. Hence, we obtain ˉψ(k)∝exp[−ikx0−(k−k0)24(Δk)2], where Δk=12Δx.
If |ψ(x)|2 is proportional to the probability density of a measurement of the particle’s position yielding the value x then it stands to reason that |ˉψ(k)|2 is proportional to the probability density of a measurement of the particle’s wavenumber yielding the value k. (Recall that p=ℏk, so a measurement of the particle’s wavenumber, k, is equivalent to a measurement of the particle’s momentum, p). According to Equation ([e2.51]), |ˉψ(k)|2∝exp[−(k−k0)22(Δk)2]. Note that this probability distribution is a Gaussian in k-space. [See Equation ([e2.46]) and Figure [f4].] Hence, a measurement of k is most likely to yield the value k0, and very unlikely to yield a value which differs from k0 by more than 3Δk. Incidentally, a Gaussian is the only simple mathematical function in x-space that has the same form as its Fourier transform in k-space.
We have just seen that a Gaussian probability distribution of characteristic width Δx in x-space [see Equation ([e2.46])] transforms to a Gaussian probability distribution of characteristic width Δk in k-space [see Equation ([e2.53])], where ΔxΔk=12. This illustrates an important property of wave-packets. Namely, if we wish to construct a packet that is very localized in x-space (i.e., if Δx is small) then we need to combine plane-waves with a very wide range of different k-values (i.e., Δk will be large). Conversely, if we only combine plane-waves whose wavenumbers differ by a small amount (i.e., if Δk is small) then the resulting wave-packet will be very extended in x-space (i.e., Δx will be large).
Contributors and Attributions
Richard Fitzpatrick (Professor of Physics, The University of Texas at Austin)

