13.14: Stern-Gerlach Experiment

Last updated
Save as PDF

Page ID: 5898

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$ \newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\id}{\mathrm{id}}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\kernel}{\mathrm{null}\,}$

$ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$

$ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$

$ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\AA}{\unicode[.8,0]{x212B}}$

$ \newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$ \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$ \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vectorC}[1]{\textbf{#1}} $

$ \newcommand{\vectorD}[1]{\overrightarrow{#1}} $

$ \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} $

$ \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} $

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$\newcommand{\avec}{\mathbf a}$ $\newcommand{\bvec}{\mathbf b}$ $\newcommand{\cvec}{\mathbf c}$ $\newcommand{\dvec}{\mathbf d}$ $\newcommand{\dtil}{\widetilde{\mathbf d}}$ $\newcommand{\evec}{\mathbf e}$ $\newcommand{\fvec}{\mathbf f}$ $\newcommand{\nvec}{\mathbf n}$ $\newcommand{\pvec}{\mathbf p}$ $\newcommand{\qvec}{\mathbf q}$ $\newcommand{\svec}{\mathbf s}$ $\newcommand{\tvec}{\mathbf t}$ $\newcommand{\uvec}{\mathbf u}$ $\newcommand{\vvec}{\mathbf v}$ $\newcommand{\wvec}{\mathbf w}$ $\newcommand{\xvec}{\mathbf x}$ $\newcommand{\yvec}{\mathbf y}$ $\newcommand{\zvec}{\mathbf z}$ $\newcommand{\rvec}{\mathbf r}$ $\newcommand{\mvec}{\mathbf m}$ $\newcommand{\zerovec}{\mathbf 0}$ $\newcommand{\onevec}{\mathbf 1}$ $\newcommand{\real}{\mathbb R}$ $\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}$ $\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}$ $\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}$ $\newcommand{\laspan}[1]{\text{Span}\{#1\}}$ $\newcommand{\bcal}{\cal B}$ $\newcommand{\ccal}{\cal C}$ $\newcommand{\scal}{\cal S}$ $\newcommand{\wcal}{\cal W}$ $\newcommand{\ecal}{\cal E}$ $\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}$ $\newcommand{\gray}[1]{\color{gray}{#1}}$ $\newcommand{\lgray}[1]{\color{lightgray}{#1}}$ $\newcommand{\rank}{\operatorname{rank}}$ $\newcommand{\row}{\text{Row}}$ $\newcommand{\col}{\text{Col}}$ $\renewcommand{\row}{\text{Row}}$ $\newcommand{\nul}{\text{Nul}}$ $\newcommand{\var}{\text{Var}}$ $\newcommand{\corr}{\text{corr}}$ $\newcommand{\len}[1]{\left|#1\right|}$ $\newcommand{\bbar}{\overline{\bvec}}$ $\newcommand{\bhat}{\widehat{\bvec}}$ $\newcommand{\bperp}{\bvec^\perp}$ $\newcommand{\xhat}{\widehat{\xvec}}$ $\newcommand{\vhat}{\widehat{\vvec}}$ $\newcommand{\uhat}{\widehat{\uvec}}$ $\newcommand{\what}{\widehat{\wvec}}$ $\newcommand{\Sighat}{\widehat{\Sigma}}$ $\newcommand{\lt}{<}$ $\newcommand{\gt}{>}$ $\newcommand{\amp}{&}$ $\definecolor{fillinmathshade}{gray}{0.9}$

This page summarizes the classic Stern-Gerlach experiment on "spin" and extends the treatment to a discussion of correlation experiments. As is often the case, I build up maximum complexity as I examine the experimental details, and then hide them in a 'box'. This time the box will turn out to be literal.

Here we concentrate on electrons, which have only two spin-states. We also mention photons, which also have two spin-states. The approach is largely based on one by Feynman which he used for objects with three spin states: see R.P. Feynman, R.B. Leighton and M. Sands, The Feynman Lectures on Physics, Vol III, Chapter 5 for this discussion.

Classical Charged Spinning Objects

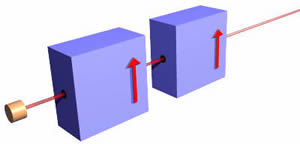
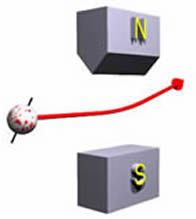
We begin by considering a macroscopic charged ball that is thrown between the poles of a magnet. If the ball is not spinning, a "knuckleball" to a baseball fan, it will not be deflected. However, if it is spinning it will be deflected as shown:

We ignore:

The weird shape of the magnet pole pieces.
The fact that there will be horizontal deflections. These can be cancelled by putting an electric field perpendicular to the plane of the ball's trajectory.

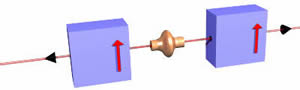
For the case shown above, the figure to the right shows the spin of the charge. We shall call this orientation "spin up" since it is deflected up by the magnets. The total amount of deflection is a function of

The total amount and distribution of electric charge on the ball.
The orientation and rate of spin. As the rate of spin increases, so does the deflection. As the axis of the spin becomes more vertical, that amount of deflection also increases.

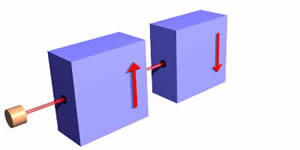
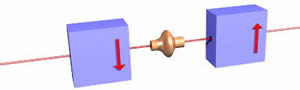
By contrast a "spin down" electron would have its spin oriented as shown below:

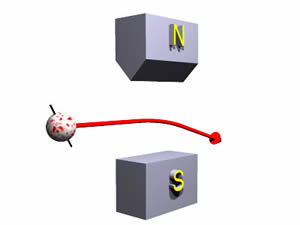
Such an object is deflected down by the magnets.

All of the above is just classical 19th century electricity and magnetism.

The Spin of the Electron

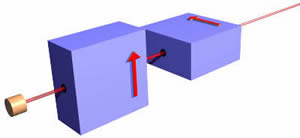
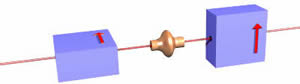
If the beam from the electron gun is directed to the magnets, as shown to the right, the beam is split into two parts. One half of the electrons in the beam are deflected up, the other half were deflected down. The amount of deflection up or down is exactly the same magnitude. Whether an individual electron is deflected up or down appears to be random. Stern and Gerlach did a version of this experiment in 1922.

This is very mysterious. It seems that the "spin" of electrons comes in only two states. If we assume, correctly, that the rate of spin, total charge, and charge distribution of all electrons is the same, then evidently the magnitude of the angle the spin axis makes with the horizontal is the same for all electrons. For some electrons, the spin axis is what we are calling "spin up", for others "spin down".

You should beware of the term "spin." If one uses the "classical radius of the electron" and the known total angular momentum of the electron, it is easy to calculate that a point on the equator of the electron is moving at about 137 times the speed of light! Thus, although we will continue to use the word "spin" it is really a shorthand for "intrinsic angular momentum."

Building a Spin Filter

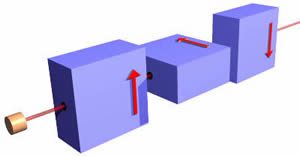
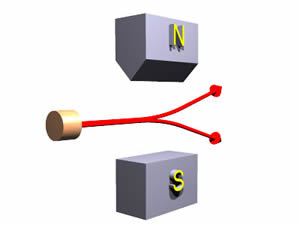
As promised at the beginning, we now make the situation a bit more complex. Consider the arrangement shown to the right:

Note that the polarity of the middle longer magnet is reversed from the other two. We have also drawn the path of a "spin up" object. When the object emerges from the magnets it is going the same direction as before it entered them with the same speed.

A Flash animation of this case may be viewed by clicking here.

The path of a "spin down" object is:

For a beam of electrons, one-half will go follow the upper path while and other half will follow the lower path:

Finally, we imagine putting a small block of lead in the path of the "spin down" electrons.

Here, one-half of the incident beam, the spin-down electrons, will be stopped inside the apparatus, while all the spin-up electrons will emerge in the same direction as before they entered the magnets and at the same speed. Thus this is a "filter" that selects spin-up electrons.

Now, again as promised, we simplify by taking all three magnets and the beam stopper and put it in a box. In the figure we also have included an electron gun firing a beam of electrons at the box. So one-half of the incident beam of electrons will emerge. It will be important to notice that we have painted an arrow on the front side of the box to indicate what direction is "up." You can't see it yet, but there is also an arrow pointing in the same direction on the back of the box.

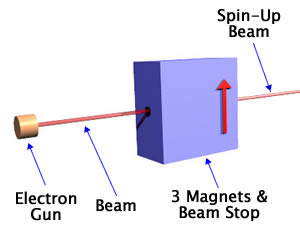
Using the Spin Filter

Note that one-half of the incident beam of electrons on the filter emerge from the box, while the other half do not. This is independent of the orientation of the filter; in all the orientations shown below one-half of the incident electrons emerge, while the other half do not.

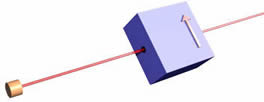
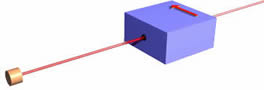
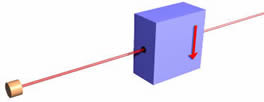
Evidently the direction of "up" is defined by the orientation of the filter doing the measurement. This is sometimes called spatial quantisation, a term I do not like.

We now put a second filter behind the first with the same orientation. The second filter has no effect. Half of the electrons from the electron gun emerge from the first box, and all of those electrons pass through the second filter. So, once "up" is defined by the first filter, it is the same as the "up" defined by the second.

Now we put the second filter behind the first and upside down relative to the first. As always, half of the beam of electrons from the electron gun emerge from the first filter, and none of those electrons emerge from the second filter. So, evidently once the first filter defines "up" that definition is the second filter's definition of "down."

Here is another orientation for the second filter, this time oriented at 90° relative to the first one.

To repeat once again, half of the beam of electrons from the electron gun emerge from the first filter. It turns out that one-half of those electrons pass through the second filter. So if we have two definitions of "up" from two filters at right angles to each other, one half of the electrons will satisfy both definitions.

If we slowly rotate the orientation of the second filter with respect to the first one from zero degrees to 180 degrees, the fraction of the electrons that passed the first filter that get through the second filter goes continuously from 100% to 0%.

Technical note: if the relative angle is A, the percentage is 100 cos²(A/2).

All of the above may remind you of polaroid filters for light. One half of a beam of light from, say, an incandescent lamp will pass through such a filter. If a second filter is placed behind the first one with the same orientation, all the light from the first filter passes through the second (at least in the case of perfect polaroid filters). A brief summary of light polarisation appears here.

If the relative orientation of the two polaroid filters for light is 90°, then no light emerges from the second filter. This corresponds to the case above for electron filters when the relative orientation is 180°.

If the relative orientation of the two polaroid filters for light is 45°, one half of the light from the first filter will emerge from the second. This corresponds to the case above for electron filters when the relative orientation is 90°.

We conclude that the only difference between electron and light filters is a factor of 2 in the relative orientations. Thus, often we call the electron filters "polarisers."

Here is a final example of combining electron filters.

One-half of the beam from the electron gun emerges from the first polariser; one-half of those electrons emerge from the second filter. And one-half of those electrons will make it through the third upside-down filter! Note that if the second filter were not present, no electrons will emerge from the upside-down filter. So we see that the middle filter actually changes the definition of "up" for the electrons. This is yet another manifestation of the Heisenberg Uncertainty Principle.

A Flash animation of up to 3 of these Stern-Gerlach filters has been prepared. It requires Flash 7, and has a file size of 130k. It will appear in a separate window. To access the animation, click here.

Correlation Measurements

We imagine a radioactive substance that emits a pair of electrons in each decay. These two electrons go in opposite directions, and are emitted nearly simultaneously. When another nucleus in the sample decays, another pair of electrons are emitted nearly simultaneously and in opposite directions. So we can have a sample emitting these pairs of electrons. To the right we show such a sample, enclosed in a copper colored device, and electron filters measuring the spin of each member of the pair:

For the radioactive substance we will be considering here, one-half of the electrons incident on the right hand filter emerge and one-half do not. Similarly, one-half of the electrons incident on the left hand filter emerge and one-half do not.

But if we look at the correlation between these electrons, we find that if, say, the right hand electron does pass through the filter, then its left hand companion does not pass its filters. Similarly, if the right hand electron does not pass through the filter, then its left hand companion always emerges from its filter.

We say that each radioactive decay has a total spin of zero: if one electron is spin up its companion is spin down. Of course, this is provided that both filters have the same definition of up.

To the right is a case where the two filters have opposite definitions of up.

Again, one-half of the right hand electrons pass through their filter and one-half of the left hand electrons pass through their filter. But this time if a particular right hand electron passes its filter, then its companion left hand electron always passes its filter. Similarly, if the right hand electron does not pass its filter, its companion electron doesn't pass through its filter either.

Now we consider yet another example. The two filters define "up" to be in perpendicular directions to each other. If you are still following this business with electron filters, you will not be surprised to learn that:

One-half of the right hand electrons emerge from their filter.
One-half of the left hand electrons emerge from their filter.
If a particular right hand electron passes its filter, one-half of the time its companion left hand electron will emerge from its filter, one-half of the time it will not.

These sorts of measurements are called correlation experiments. We show an arbitrary relative orientation of the two filters.

We summarise all of the above by saying that when the two filters have the same orientation, the correlation is zero: if the right hand electron passes its companion does not. When the two filters have opposite orientations, the correlation is 100%: if the right hand electron passes, so does its companion, while if the right hand electron does not pass, neither does its companion. When the two filters have perpendicular orientations, the correlation is 50%. It turns out that the correlation goes smoothly from zero to 100% as the relative orientation goes from 0° to 180°. For the mathphilic student, the actual formula is that the correlation is sin(a/2) squared, where a is the relative angle between the filters.

There are radioactive substances that emits pairs of photons similar the the pairs of electrons we have been consider so far. Some such substances have similar correlations to the electron source we have been considering, except that there is a difference of a factor of two in the relative orientations of the polarisers. If the light polarisers have the same orientation, the correlation is zero; this is the same as for electrons.

If the light polarisers have a relative orientation of 90°, the correlation is 100%: if the right hand photon passes through its polariser it companion photon will pass its polarisers, while if the right hand photon does not pass, neither does its companion. This corresponds to the case for electrons where the relative orientation of the filters was 180°.

Similarly, if you are still following all this, the correlation when the relative orientation of the light polarisers is 45° is 50%, just the correlation for electron with relative filter orientations of 90°.

As we shall see these correlation experiments, both for electrons and photons, have been performed and turn out to give us important information about the way the world is put together. This is the thrust of Bell's Theorem, also sometimes known as the Einstein-Podolsky-Rosen (EPR) paradox.

Author

This document was written by David M. Harrison, Department of Physics, University of Toronto, mailto:harrison@physics.utoronto.ca in March 1998. This is $Revision: 1.26 $, $Date: 2006/03/12 18:11:55 $ (y/m/d UTC).

Search

Text Color

Text Size

Margin Size

Font Type